5.5.1. Измерение значения физических величин.

В учебных опытах, как правило, ставится задача измерения значения физической величины, которое уже известно науке из ранее проведенных опытов. Это, например, учебные эксперименты по определению значения ускорения свободного падения, заряда электрона, постоянной Планка и многие другие.

Учебная цель подобных экспериментов состоит в освоении методики измерения, приобретении навыков осуществления операций измерения, приобретения умения пользоваться различными измерительными приборами. Содержание учебного опыта типично: осуществляется измерение значения заданной физической величины, сравнение его с известным (табличным или расчетным), оценка погрешности измерения и его достоверности (степени доверия к результатам измерения).

Часто перед измерением проводят оценку значения физической величины. Оценка – приближенное, примерное значение физической величины. Задача оценки – «навскидку», быстро, без громоздких расчетов или трудоемких точных («прецизионных») измерений определить ожидаемое значение физической величины. Обычно для оценки используют упрощенные модели, допускают серьезные пренебрежения различными факторами.

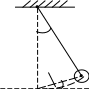
В качестве примера оценим значение периода колебаний математического маятника (рис. 20). Пусть в начальный момент времени маятник находится в точке А; точка В – положение равновесия. Тогда период колебаний есть учетверенный промежуток времени, за который маятник пройдет дугу АВ. Для оценки заменим истинное движение по дуге окружности движением по прямой – по хорде АВ. Тогда движение маятника можно рассматривать как соскальзывание по наклонной плоскости, угол которой с горизонтом оставляет α/2. При этом ускорение равно Длина наклонной плоскости (хорды АВ) где L – длина нити. С другой стороны, перемещение ℓ при равноускоренном движении с ускорением а определяется как , откуда находим время движения по хорде и период колебаний

α L

А

α /2

В

Рис. 20. К оценке значения периода математического маятника.

Известная из теории формула для расчета периода малых колебаний -

формула Гюйгенса – имеет вид:

В результате оценки получаем, что период колебаний зависит от , однако неточно определено значение численного коэффициента (8 ≠ 2π).

Численное значение периода Т (при длине маятника 1 м, ):

- по произведенной оценке: с.

- расчетное значение по формуле Гюйгенса: с.

Абсолютная погрешность оценки ΔТ = 0,6 с. Погрешность достаточно большая, но задача оценки выполнена, т.е. порядок величин совпадает.

5.5.2. Экспериментальное установление вида зависимости между двумя (или более) физическими величинами.

В учебных опытах эта задача формулируется обычно как экспериментальная «проверка» какого-либо физического закона (или формулы).

Рассмотрим в качестве примера экспериментальную «проверку» закона Бойля – Мариотта (лабораторная работа №.).

Выражение для закона Бойля – Мариотта, описывающего изотермический процесс, имеет вид рV = const (или р₁V₁ = р₂V₂) при T = const. Таким образом, закон утверждает, что произведение давления газа на его объем при постоянной температуре постоянно. Представим, что это гипотеза. Для её проверки в эксперименте необходимо прямыми измерениями получить несколько пар значений параметров исследуемой физической системы «идеальный газ» – давления р_i и объема газа V_i при определенной неизменной температуре. Пусть границы абсолютных Т погрешностей измерений давления и объема в данном эксперименте равны, соответственно, ±∆р и ±∆V. Нанесем полученные три пары значений в виде заштрихованных зон и расчетную кривую, построенную по уравнению рV = const на график рис.21).

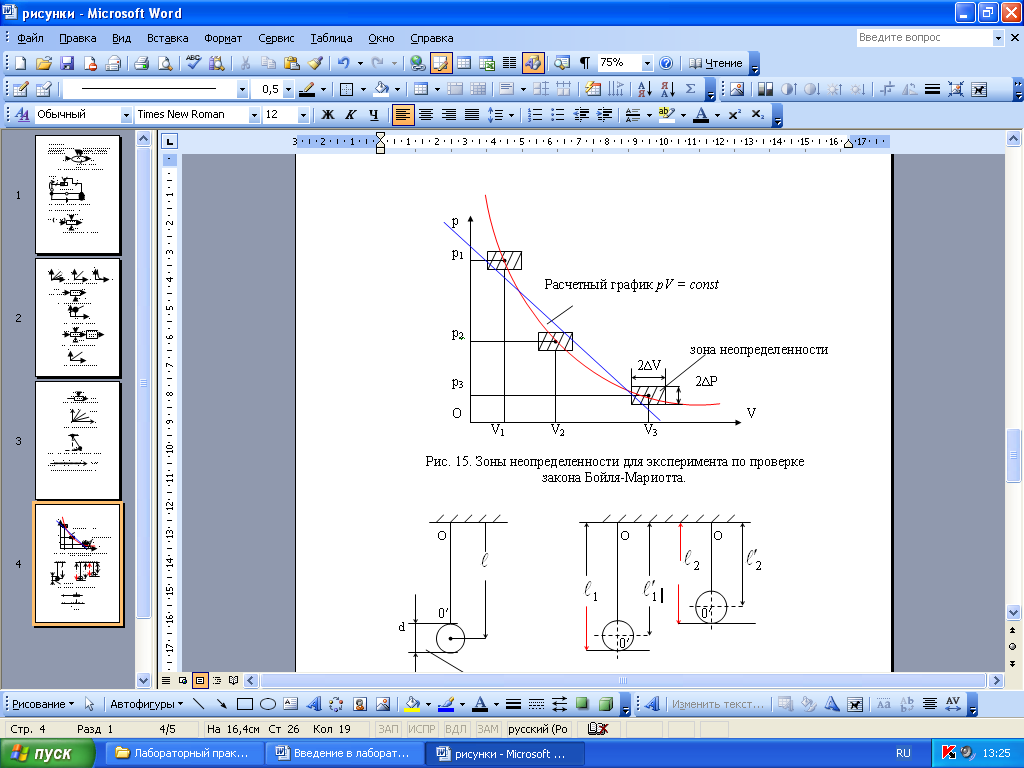
Рис. 21. К примеру экспериментальной «проверки» закона Бойля-Мариотта.

Заштрихованные прямоугольники соответствуют зонам неопределенности полученных значений произведений трех пар р_iV_i; это означает, что действительные (истинные) значения произведения рV находятся в пределах этих зон. Из графика следует, что в данном опыте, при данных погрешностях измерения ∆р и ∆V гипотеза о том, что рV = const не подтверждается. Дело в том, что через зоны неопределенности можно провести, например и прямую линию (см. рис. 21). Для подтверждения «гипотезы» нужно повысить точность (уменьшить погрешность) измерения давления и объема. (В идеале зоны неопределенности при нулевых погрешностях ∆р и ∆V стягиваются в точки).

В качестве примера использования совокупных измерений, рассмотрим определение ускорения свободного падения по измеренному значению периода колебаний математического маятника. Это косвенное измерение. В эксперименте математический маятник - небольшой тяжёлый шарик - подвешен на достаточно длинной нити (рис. 22).

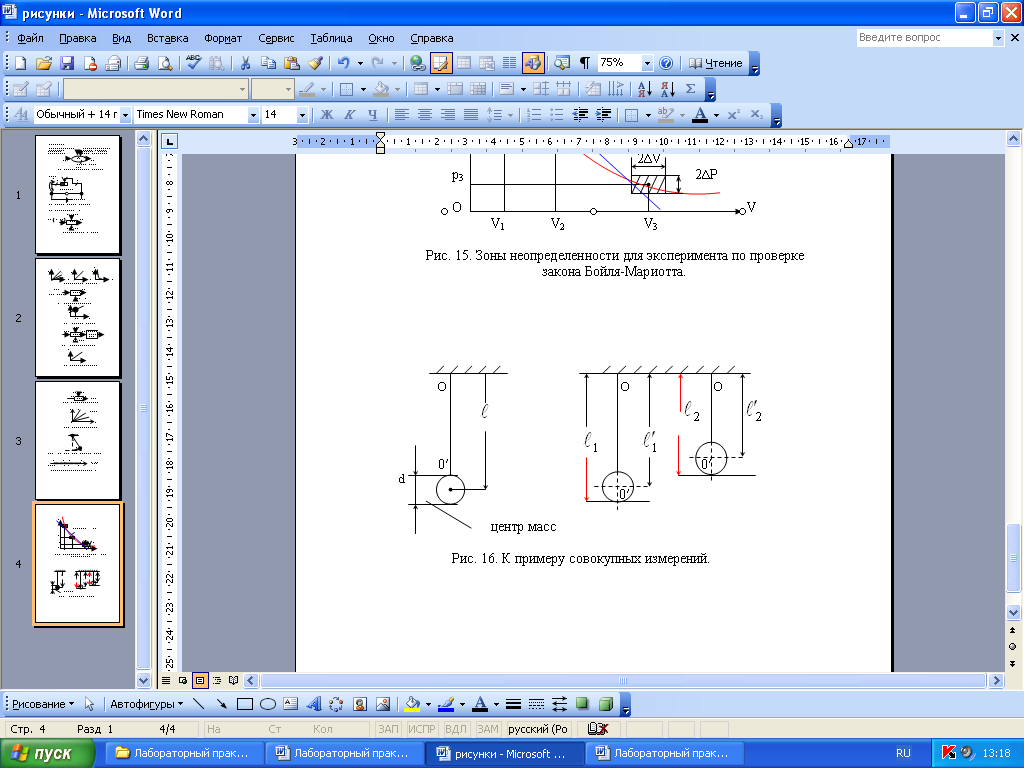
Рис. 22. К примеру совокупных измерений.

Ускорение свободного падения g из формулы Гюйгенса может быть определено как

.

Здесь Т – период колебаний маятника; - длина маятника – расстояние от точки подвеса О до центра масс (тяжести) 0′ маятника. Шарик имеет диаметр d; достаточно точно измерить значение сложно из-за трудности определения центра масс шарика. В этом случае целесообразно осуществить два измерения при разных длинах маятника ; значение g в обоих опытах одинаково, тогда (для определённости ) получим

; , откуда

;

Из рисунка 22 видно, что ; .

и - расстояние от точки подвеса до центра масс.

Т огда , и

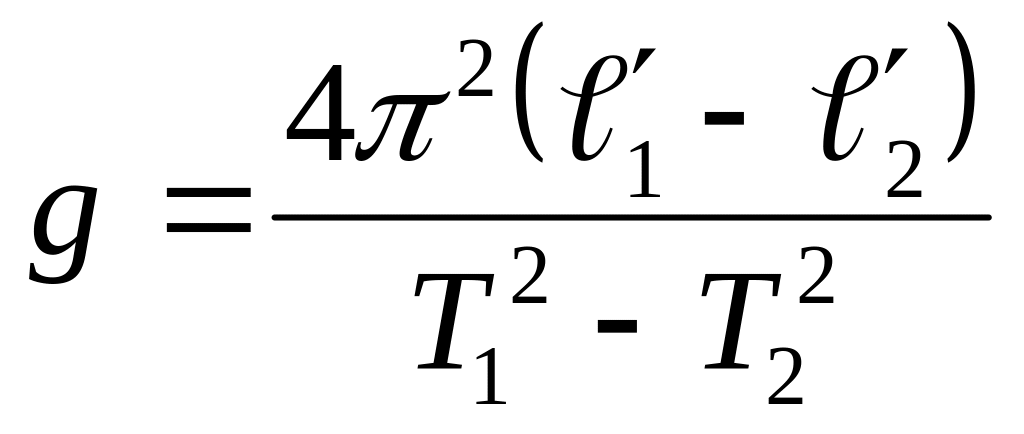
Использование временно́й избыточности (дополнительного измерения) позволило устранить влияние неточности измерения диаметра шарика и заменить измерение расстояний до центра масс шарика измерением разности длин от точки подвеса до нижней точки шарика. Цена повышения точности – проведение двух измерений ( и ) вместо одного (ℓ). При решении вопроса о введении избыточности, т.е. использовании совокупных измерений, следует сравнить получаемый выигрыш в точности и затраты на проведение дополнительных измерений.