Глава 5. Статистика заработной платы

Заработная плата - это часть валового внутреннего продукта, поступающего в личное потребление работников из средств, выделенных на оплату труда.

Фонд заработной платы определяется начисленной суммой выплат в денежной и в натуральной формах за выполненный объем работ, за проработанное время, а также за неотработанное время, подлежащее оплате в соответствии с действующими положениями по труду.

В состав фонда заработной платы включаются следующие виды выплат: оплата труда за выполненный объем работ и за отработанное время; выплаты стимулирующего характера; выплаты компенсирующего характера, связанные с режимом работы и условиями труда; оплата за неотработанное время; другие выплаты, включаемые в состав фонда заработной платы.

Пример 5.1. Денежные и натуральные выплаты работникам строительной организации в текущем периоде характеризуются следующими данными (млн. руб.):

1.	Заработная плата, начисленная по сдельным расценкам и тарифным ставкам	104300
2.	Сумма индексации заработной платы в связи с повышением цен на товары и услуги	1700
3.	Оплата брака, допущенного не по вине рабочих.	380
4.	Оплата труда студентов учебных заведений, проходящих производственную практику (расчет за выполненную работу производился непосредственно со студентами)	10
5.	Надбавки к тарифным ставкам за профессиональное мастерство	1050
6.	Вознаграждения по итогам годовой работы	7300
7.	Надбавки за подвижной характер работы	36
8.	Оплата за работу в выходные и праздничные дни	7
9.	Доплаты за работу в зонах радиоактивного загрязнения	31
10.	Оплата трудовых и дополнительных отпусков	13400
11.	Оплата времени вынужденных прогулов	52
12.	Стоимость бесплатно предоставленного питания	12
13.	Оплата проезда к месту работы транспортом организации	18
14.	Оплата проживания работников в общежитии организации	23

Определить фонд заработной платы, распределив его по видам оплаты.

Общий фонд заработной платы включает все виды выплат, приведенные в условии задачи. Отсюда:

F = 104300+1700+380+10+1050+7300+36+7+31+13400+52+12+18+23 = 128319 млн. руб.

в том числе:

Выплаты за выполненный объем работ и отработанное время:

104300+1700+380+10 = 106390 млн. руб.

Стимулирующие выплаты:

1050+7300 = 8350 млн. руб.

Выплаты компенсирующего характера:

36+7+31= 74 млн. руб.

Оплата за неотработанное время:

13400+52 = 13452 млн. руб.

Другие выплаты:

12+18+23 = 53 млн. руб.

Уровень оплаты труда характеризуется показателем средней заработной платы. Различают среднюю часовую, дневную, месячную (квартальную, годовую) заработную плату. Их расчет производится по формулам:

где f_ч, f_д и f_м - показатели соответственно среднечасовой, среднедневной и среднемесячной заработной платы;

F_ч, F_д и F_м - соответственно часовой, дневной и месячный фонды заработной платы;

Т_ч, T_д, - число отработанных соответственно человеко-часов, человеко-дней и среднесписочной численности работников за месяц.

Пример 5.2. Часовой фонд заработной платы рабочих строительной организации составил 375200 тыс. руб., дневной - 420300 тыс. руб., месячный - 508350 тыс. руб. Среднесписочная численность рабочих за месяц составила 1520 человек, ими отработано 36150 чел. - дней и 250320 человеко-часов.

Рассчитаем показатели средней заработной платы.

f_ч = 375200 : 250320 = 1,49888 тыс. руб.

f_д = 420300 : 36150 = 11,626 тыс. руб.

f_м = 508350 : 1520 = 334,4 тыс. руб.

Между показателями средней заработной платы существует следующая взаимосвязь:

f_м = f_ч  t_д  K_д  t_м  К_м ,

где t_д и t_м - показатели соответственно средней продолжительности рабочего дня и рабочего месяца.

K_д и К_м - соответственно коэффициенты доплат в дневном и в месячном фондах заработной платы.

Покажем взаимосвязь между показателями средней заработной платы, при условии, что средняя продолжительность рабочего дня составила 6,924 час., средняя продолжительность месяца - 23,78 дня. Рассчитаем коэффициенты доплат в фондах заработной платы:

K_д = F_д : F_ч = 420300 : 375200 = 1,12;

К_м = F_м : F_д = 508350 : 420300 = 1,21

Отсюда:

334,4 = 1,49888  6,924  1,12  23,78  1,21

Если предположить, что месячный фонд заработной платы в базисном периоде составил 430720 тыс. руб., а численность рабочих возросла на 1,2%, то можно определить прирост фонда заработной платы и разложить прирост по факторам. В примере:

F= 508350 - 430720 = 77630 тыс. руб.

в том числе за счет:

увеличения численности работников:

F_т = F₀(I_т - 1) = 430720(1,012-1) = 5168,64 тыс. руб.

повышения средней заработной платы:

508350

F_f = F₀(I_F - I_T ) = 430720(---------- - 1,012)=430720(1,180233-1,012)=

430720

=430720  0,168233=72461,317 тыс. руб.

F = F_т+F_f = 5168,64+72461,317=77629,99 тыс. руб.

Заработная плата работников строительных организаций определяется множеством факторов, которые обусловливают ее вариацию и дифференциацию работников по уровню оплаты труда. Для оценки дифференциации работников рассчитывают показатели вариации, непараметрические средние (моду, медиану, нижний и верхний квартили).

Пример 5.3. Распределение работников строительной организации по размеру заработной платы в текущем периоде характеризуется следующими данными:

Группы работников по размеру заработной платы, тыс. руб.	Число работников
до 40	70
40-60	100
60-80	140
80-100	150
100-120	90
120-140	40
140 и выше	10
Всего	600

Рассчитать: 1) среднюю заработную плату; 2) дисперсию, среднее квадратическое отклонение и коэффициент вариации; 3) моду и медиану, нижний и верхний квартили, коэффициент асимметрии.

Построим таблицу, в которой выполним необходимые расчеты для определения средней и дисперсии.

Группы работн. по размеру . зар. платы, тыс. руб.	Число работников	Середина интервала (Х)	Х-А А=90	i=20				Накопленные частоты
До 40	70	30	-60	-3	-210	9	630	70
40-60	100	50	-40	-2	-200	4	400	170
60-80	140	70	-20	-1	-140	1	140	310
80-100	150	90	0	0	0	0	0	460
100-120	90	110	20	1	90	1	90	550
120-140	40	130	40	2	80	4	160	590
140 и выше	10	150	60	3	30	9	90	600
Итого	600	-	-	-	-350	-	1510

тыс. руб.

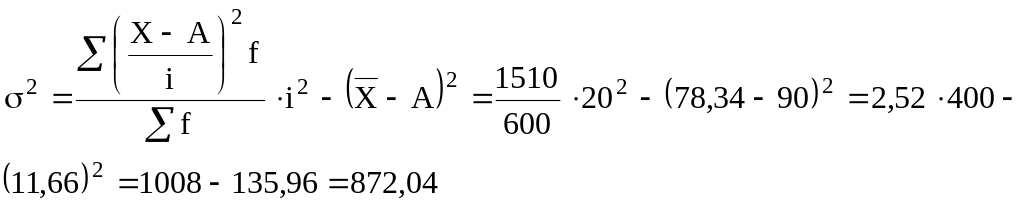
тыс. руб.

Таким образом, средняя заработная плата составила в расчете на одного рабочего 78,34 тыс. руб.; среднее квадратическое отклонение 29,5 тыс. руб., коэффициент вариации 37,7%, указывая на неоднородность рабочих по уровню оплаты труда.

Рассчитаем моду, медиану, нижний и верхний квартили:

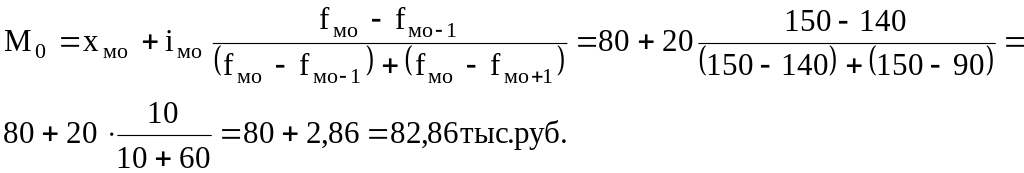
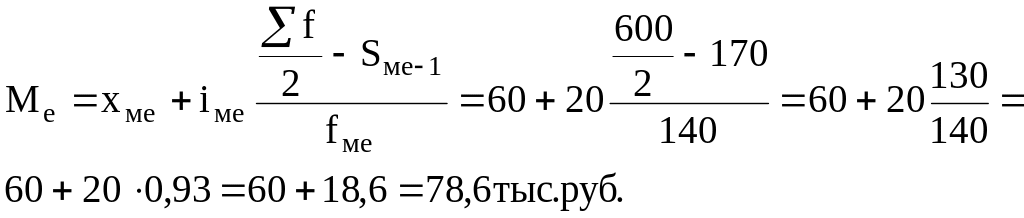
Мода показывает, что в строительной организации наиболее часто встречаются работники с уровнем заработной платы в 82,86 тыс. руб. Медиана указывает на то, что половина рабочих получала в текущем периоде до 78,6 тыс. руб., а вторая половина – свыше 78,6 тыс. руб.

Для расчета нижнего и верхнего квартилей необходимо определить

и числа работников в группах, расположенных сверху. Нижний квартиль, отсекающий ¼ сверху, расположен во второй группе в интервале

40-60, т. к. доля двух верхних групп составила 0,28, (170 : 600) = 0,28, что немногим больше ¼, а верхний квартиль расположен в интервале 80-100 (460 : 600) = 0,77. Отсюда:

Таким образом четверть рабочих или 25% получают в среднем до 56 тыс. руб., еще одна четверть свыше 98,6 тыс. руб., а половина рабочих – от 56 до 98,6 тыс. руб.

Рассчитаем коэффициент асимметрии (К_А)

Имеет место небольшая левосторонняя или отрицательная асимметрия.

Фонд заработной платы зависит не только от оплаты труда за выполненный объем работ и отработанное время, но и от различного рода надбавок и доплат в форме выплат стимулирующего характера и др. Оценку влияния доплат на размер и динамику фонда заработной платы можно дать путем построения и решения следующей мультипликативной индексной модели.

где F_м – фонд месячной заработной платы

F_р – оплата за выполненный объем работ и за отработанное время

F_c, F_к, F_н, F_д – соответственно выплаты стимулирующего , компенсирующего характера, за неотработанное время, другие выплаты.

Каждая дробь модели представляет собой коэффициент доплат в фонде заработной платы за счет соответствующего вида выплат. Для упрощения модели представим ее следующим образом:

F_м=F_рК_сК_кК_нК_д, где К_с, К_к, К_н, К_д – соответственно коэффициенты доплат в фонде заработной платы за счет стимулирующих выплат (К_с), выплат компенсирующего характера (К_к), оплаты за неотработанное время (К_н), других выплат (К_д).

Решим приведенную модель, используя данные задачи 5.1.Рассчитаем соответствующие коэффициенты доплат:

К_с(1)= (106390 + 8350) : 106390 = 114740 : 106390 = 1,078485

К_к(1)= (114740 + 74) : 114740 = 114814 : 114740 = 1,000645

К_н(1)= (114814 + 13452) : 114814 = 128266 : 114814 = 1,117163

К_д(1)= (128266 + 53) : 128266 = 128319 : 128266 = 1,000413

Отсюда: F_м(1) = 106390 1,078485 1,0006451,1171631,000413 = 128319 млн. руб.

Предположим, что соответствующие показатели в базисном периоде составили:

F_р(0) = 80100, К_с(0)= 1,062, К_к(0)= 1,022, К_н(0)= 1,109, К_д(0)= 1,0012, а

F_м(0) = 801001,0621,0221,1091,0012 = 96529,6 млн. руб.

Индексная модель динамики фонда заработной платы:

или приняв соответствующие обозначения:

Рассчитаем индексы соответствующих показателей-факторов:

Индекс выплат за выполненный объем работ и отработанное время:

I_а = 106390 : 80100 = 1,328215

Индекс коэффициента доплат за счет стимулирующих выплат:

I_b = 1,078485 : 1,062 = 1,0155

Индекс коэффициента доплат за счет выплат компенсирующего характера:

I_с = 1,000645 : 1,022 = 0,9791

Индекс коэффициента доплат за счет оплаты неотработанного времени:

I_d = 1,117163 : 1,109 = 1,0074

Индекс коэффициента доплат за счет других выплат, включаемых в состав фонда заработной платы:

I_k = 1,000413 : 1,0012 = 0,99921

Индекс месячного фонда заработной платы:

I_F = 128319 : 96529,6 = 1,329 или

I_F = 1,328215 1,0155  0,9791  1,0074  0,99921 = 1,329

Решим модель индексным методом с учетом того, что на первом месте в модели стоит объемный показатель.

Абсолютный прирост фонда заработной платы составил:

F = 128319 – 96529,6 = 31789,4 млн. руб.

в том числе:

F_а = F₀ (I_a- 1) = 96529,6 (1,328215 – 1) = 31682,4 млн. руб.

F_b = F₀ I_a(I_b- 1) = 96529,6  1,328215 (1,0155 – 1) = 1987,26 млн. руб.

F_c = F₀ I_aI_b(I_c- 1) = 96529,6  1,328215  1,0155 (0,9791 – 1) = - 2721,2 млн. руб.

F_d = F₀ I_aI_bI_c(I_d- 1) = 96529,6  1,328215  1,0155  0,9791 (1,0074 – 1) = 943,3 млн. руб.

F_к = F₀ I_aI_bI_cI_d(I_к- 1) = 96529,6  1,328215  1,0155  0,9791  1,0074 (0,99921 – 1) = -101,45 млн. руб.

Таким образом общий прирост составил:

F = 31682,4 + 1987,26 + (-2721,2) + 943,3 + (-101,45) = 31790,3 млн. руб.

Определим влияние каждого фактора на изменение фонда заработной платы в относительном выражении. Общая величина прироста (I_F) составила:

I_F = I_F – 1 = 1,329 – 1 = 0,329 или 32,9%.

Разложим темп прироста по факторам:

или 32,82%.

или 2,1%.

или -2,8%.

или 0,97%.

Отсюда:

I_F = 32,8+2,1+(-2,8)+0,97+(-0,11) = 32,9%

Определим долю каждого фактора в общем приросте фонда заработной платы (экономическую значимость фактора):

или

или

Сумма долей должна равняться 100%

99,7+6,3+(-8,6)+2,97+(-0,32) = 100,05%.

Представим результаты расчетов в аналитической таблице.