4. Для построения диаграммы выделим ячейки a1 –b24,затем нажмем Вставка – Диаграмма – График –Enter,получим следующий вид рис.3 рис.3 – Метод золотого сечения
5. Из таблицы4 и рис3 видно,что наименьшее значение функции достигается в точке x=-0,646
Встроенная подпрограмма EXCEL “Поиск решения”.
EXCEL имеет специальную подпрограмму, позволяющую решать многие оптимизационные задачи, в том числе и задачи одномерной оптимизации.
Будем искать решение на том же рабочем листе. 1. Выделим ячейку А59 для значений независимой переменной Х, а ячейку В59 - для значений целевой функции f(X).
2.Занесем в ячейку В59 формулу =2*A59^3+12*A59^2+13*A59+15
3.Запустим подпрограмму, с помощью команды меню Сервис- Поиск решения. В поле Установить целевую ячейку занесем адрес В59, с помощью переключателей в левой части диалога установим режим поиска минимального значения в этой ячейки. В поле Изменяя ячейки занесем адрес А59 и в списке Ограничения укажем дополнительные условия нахождения минимума c помощью кнопки Добавить. (см рис4).Далее кнопка Выполнить. В ячейке А59 получим решение = -0,646
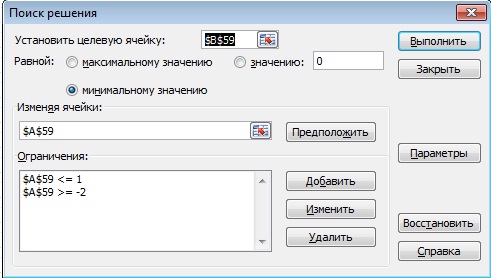
Рис4 – Поиск решений
Заключение.
Таким образом, мы решили задачу одномерной оптимизации, где использовали методы: дихотомии и золотого сечения, а правильность наших действий мы проверили с помощью подпрограммы «Поиск решений» программы «Excel». Все три значения оказались одинаковыми, следовательно, задача решена верно.