Требуется определить оптимальную загрузку машин (программу) с использованием критерия – минимальные издержки производства

Заданы технологические и стоимостные коэффициенты (нормативные параметры модели):

производительность				Стоимость ед. времени
аij	Тип машины j			bij	Тип машины j
	j=1 j =2		j=1 j =2
i =1	6	13	Вид продукции i	i =1	4	13
i =2	24	13		i =2	47	26

Условия задачи

Ограничения на искомые переменные : 0 =< x_ij =< 6 для _ij

Время работы –

1 маш. : f1= x₁₁ + x₂₁ =< 6;

2 маш. : f2=x₁₂ + x₂₂ =< 6

Объем 1 прод. - f3=а₁₁x₁₁ + а₁₂x₁₂ = N₁ = 30

Объем 2 прод. - f4=а₂₁x₂₁ + а₂₂x₂₂ = N ₂ = 96

Критерий оптимизации производственного плана – производственной программы

Цена заказа - F = b₁₁x₁₁ + b₁₂x₁₂ + b₂₁x₂₁ + b₂₂x₂₂ min

Выпишем все алгебраические зависимости, представляющие модель в целом:

min F = b₁₁x₁₁ + b₁₂x₁₂ + b₂₁x₂₁ + b₂₂x₂₂;

f1= x₁₁ + x₂₁ =< Т;

f2= x₁₂ + x₂₂ =< Т;

f3= а₁₁x₁₁ + а₁₂x₁₂ = N₁;

f4= а₂₁x₂₁ + а₂₂x₂₂ = N₂;

f5= x₁₁>=0;

f6= x₂₁>=0;

f7= x₁₂ >=0;

f8= x₂₁>=0;

N₁ = 30;

N₂ = 96;

T= 6.

x₁₁ и x₂₁ - приняты как базисные переменные (минимальное порождающее подмножество).

x₁₂ и x₂₂- небазисные переменные, получаемые через базисные x₁₁ и x₂₁.

Вывод о типе модели математического программирования – это модель линейного программирования.

Для представления графического вида симплекса (через базисные переменные) выполним Формальные преобразования:

Из всех алгебраических зависимостей исключаются небазисные переменные (x₁₂ и x₂₂)

F = 222 - 2 x₁₁ - x₂₁

x₁₁>=0 (1), x₂₁>=0 (2), x₁₁=< 5 (3), x₂₁=< 4 (4)

x₁₁+ x₂₁ =< 6 (5), x₁₁+ 4x₂₁ => 8 (6),

Графический образ симплекса модели линейного программирования для распределения производственных мощностей

Симплекс модели линейного программирования – n-мерный многогранник, симплициальный комплекс, выпуклая оболочка – в линейном программировании область допустимых решений, каждая точка внутри симплекса является допустимым решением системы уравнений и неравенств, представляющих математическую модель.

x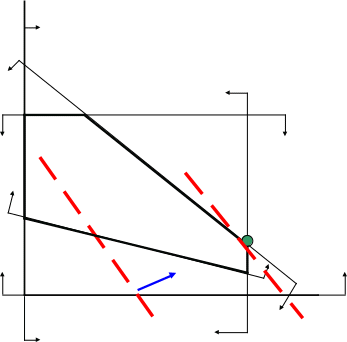 ₂₁

(3)

(4)

F₀

(x₁₁=5; x₂₁=1)

(6)

(5)

(

F→min

2)

F→min x₁₁

(1)

Решение задачи: minF = 211

x₁₁=5; x₂₁=1;

f3= а₁₁x₁₁ + а₁₂x₁₂ = N₁; x₁₂ = (1/а₁₂)(N₁(30) - а₁₁x₁₁) = 30/13 – (6/13)5 = 0;

f4= а₂₁x₂₁+а₂₂x₂₂ =N₂; x₂₂ = (1/а₂₂)(N₂(96) – а₂₁x₂₁) =96/13–(24/13)1 = 5,54

а₂₂ = 13 а₂₁= 24 72/13 =

Второй этап — определение и исследование математических задач, к которым приводит востребованная математическая модель, т.е. тех математических технологий, которые лягут в основу вычислительной (рекурсивной) схемы модели.

3 шаг. Третья Лингвистическая форма математической модели (на языке программирования для ЭВМ, символьный формат, символьный формат, в символах языка программирования)

Используем современный индустриальный подход к проектированию математической модели. С этой целью используем аналитическую вычислительную среду прикладного инструментального пакета Excel

В операторных символах прикладного пакета Excel