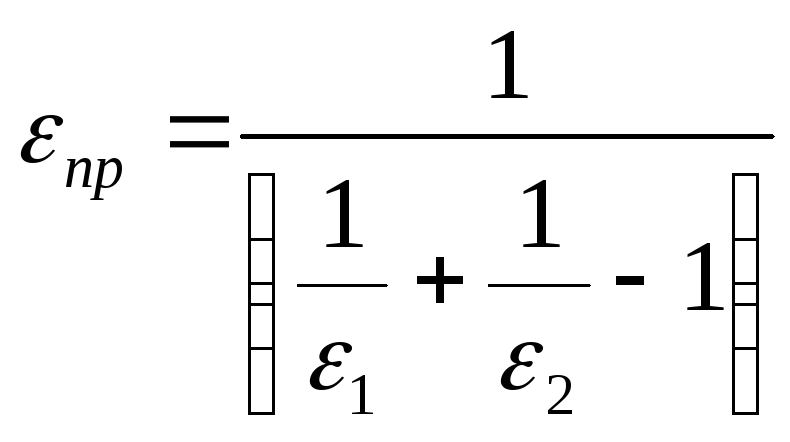- •1 Закон тд для закр. Неподвиж. Сис-мы.
- •1Ый з-н термодинамики для закрытой подвижной системы
- •I з-н тд для открытой системы(стационарного поточного процесса.
- •2Ой з-н термодинамики:
- •Круговые проц или Циклы :
- •Дросселирование газов
- •Необратимые термодинамические процессы
- •Обратимые и необрат процессы
- •ПОлитропные процессы ид.Газа
- •Термич.Поле. Градиент температуры.
- •Механизмы и законы переноса теплоты. Явление теплопроводности, теплоотдачи и излучения.
- •Тепловая хар-ка обратимых циклов.
- •Теплообмен излучением
- •Основные понятия ти
- •Законы теплообмена излучения.
- •1.Физ. Условия теплообмена конвекцией.
- •2,Факторы, определяющие интенсивность конвективного теплообмена.
- •Теплоптоводность ч/з многослойную цил-ую стенку.
- •Теплоптоводность ч/з цил-ую стенку.
- •Цикл Карно (цк). Теорема Карно.
- •2Ой случай
- •3Ий случай
- •Цикл Отто.
- •Цикл Дизеля.
- •Теплопередача через многослойную цилиндрическую стенку.
- •Критический диаметр тепловой изоляции трубопровода.
- •Факторы определяющие интенсивность конвективного теплообмена.
- •Числа подобия процессов конвективного теплообмена.
Цикл Карно (цк). Теорема Карно.
Ц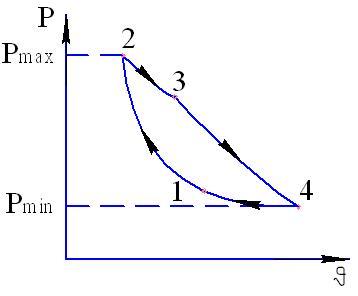 икл
Карно предложен в 1824г. Это обратимый
цикл. Прямой ЦК состоит из 4-х обратимых
процессов:
икл
Карно предложен в 1824г. Это обратимый
цикл. Прямой ЦК состоит из 4-х обратимых
процессов:
1-2 – адиабатич.сжатие;
2-3 – изотермич.расширение;
3-4 – адиабатич.расширение;
4-1 - изотермич.расширение.
Используя св-ва процессов устанавливаем, что: T1=T4; T2=T3; q12=q34. Для газообразного раб.тела при его небольших скоростях ф-лу (1.30) можно переписать в виде: qij-lij=ij-ii (1.34).i-начальная т-ка, j – конечная т-ка процесса.
Для адиабатического сжатия и расширения: -l12= i2-i1=cp(T2-T1) ; -l34= i4-i3= -(i3-i4)=-cp(T2-T1) ; l34=-l12 => обе эти работы взаимокомпенсируются в цикле. Поэтому полезная работа цикла будет определяться только разносью мех.работ в изотермич.процессах расширения и сжатия. q23-l23= i3-i2= cp(T3-T2)=0 ; q41-l41= i1-i4= cp(T1-T4)=0 или
![]() ;
;
![]() .
.
![]() (1.35).
(1.35).
Процессы 1-2 и 3-4 адиабатные, уравнение адиабаты:
pvk=C1
или, используя
газовый з-н получим: p=CTk/(k-1).
Поэтому
отношение давлений для этих процессов
равны:
![]() ,
для к-х справедливо (1.34). Вычислим
отношения давлений в 1.35:
,
для к-х справедливо (1.34). Вычислим
отношения давлений в 1.35:![]() (1.37).
(1.37).
Термический КПД по ЦК определим из 1.34:
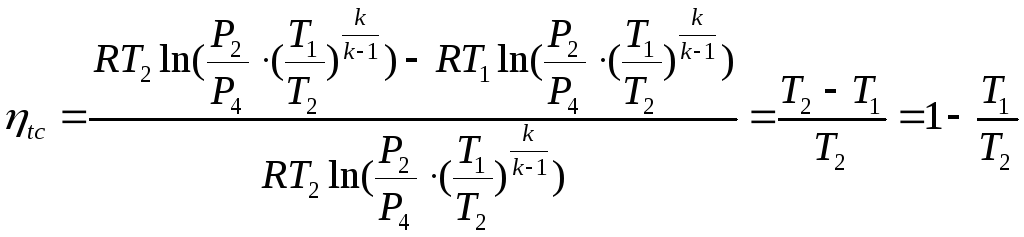 .
Из полученной формулы видно, что КПД
ЦК, совершаемого идеальным газом зависит
только от макс.и миним.температур газа
в цикле. На основании этого теорема
Карно: термический КПД ЦК не зависит от
св-в раб.тела и определяется только
температурами высшего и низшего
источников теплоты.
.
Из полученной формулы видно, что КПД
ЦК, совершаемого идеальным газом зависит
только от макс.и миним.температур газа
в цикле. На основании этого теорема
Карно: термический КПД ЦК не зависит от
св-в раб.тела и определяется только
температурами высшего и низшего
источников теплоты.
Частные случаи политропных процессов.
Изобарный P=const . Из
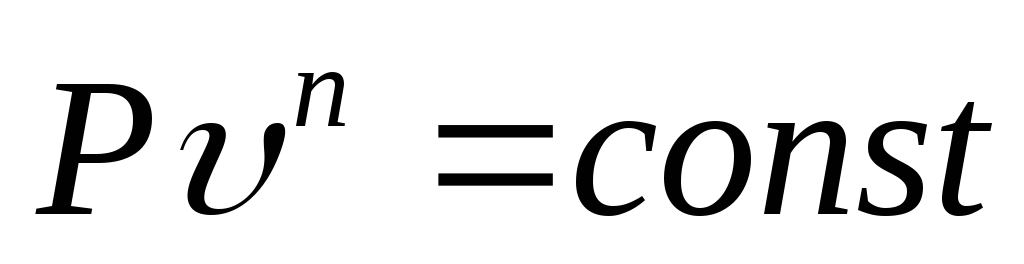

 ,n=0.
Из
,n=0.
Из
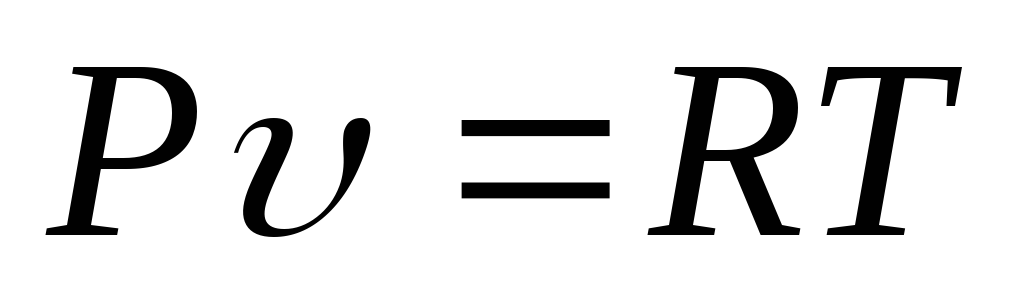 получим 1 закон Гей-Люссака:
получим 1 закон Гей-Люссака: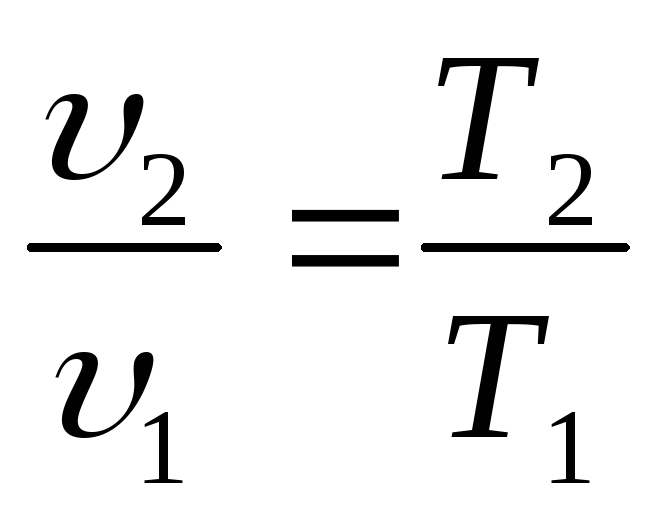 .
Из
.
Из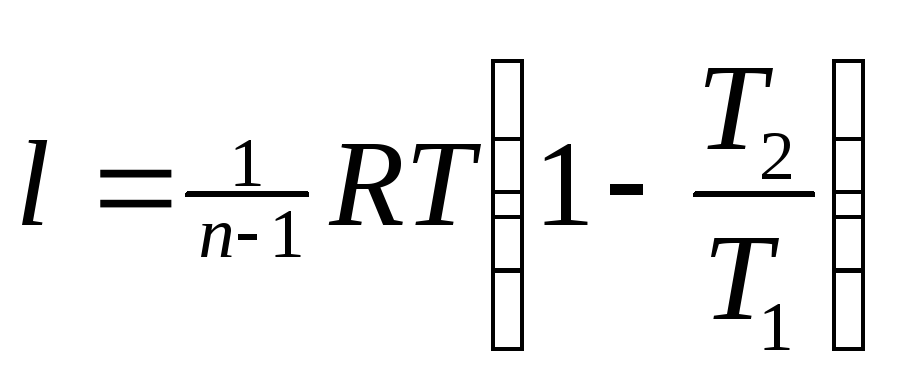

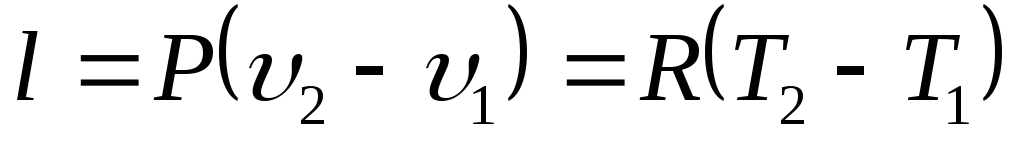
Теплоемкость и
подведенная теплота соответственно
равны:
![]() ;
;![]() ;
;![]()
Изохорный
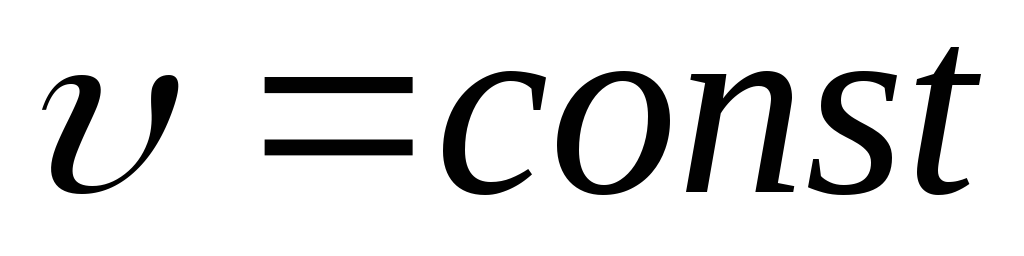
![]() ,
,![]() ,
,![]()
![]() ;
;
![]() ;
;
![]()
Т.к.
![]() то газ работу расширения не совершает,
поэтому вся теплота идет на изменение
внутренней энергии но
то газ работу расширения не совершает,
поэтому вся теплота идет на изменение
внутренней энергии но![]() -
распологаемая энергия.
-
распологаемая энергия.
![]()
Изотермический T=const
Из
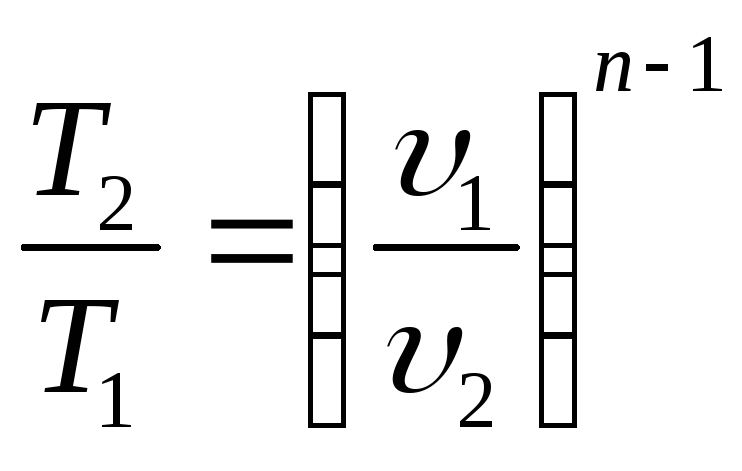
![]() n=1
, а из
n=1
, а из
![]() закон Бойля-Мариотто
закон Бойля-Мариотто![]()
![]()
du=0
, dq=d![]() Вся теплота идет в работу изменения
объема
Вся теплота идет в работу изменения
объема
![]() Из
Из
![]()
![]() С=
С=![]()
![]()
Адиабатный процесс dq=0
dq=CdT=0 нужно чтобы С=0 или n=k.
![]() или
или
![]()
![]() или
или
![]()
![]()
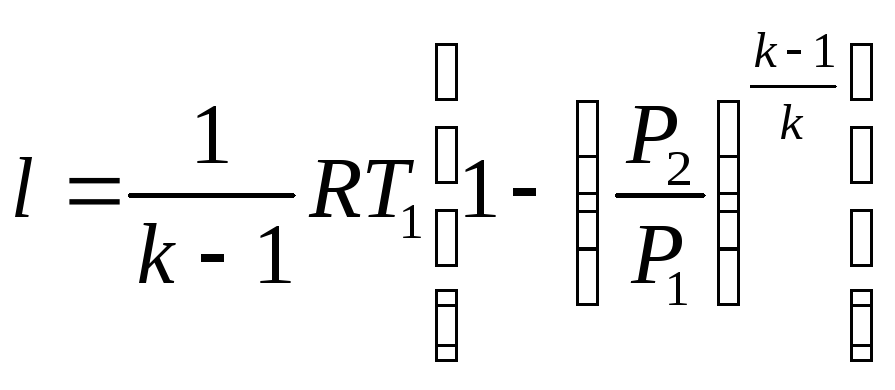 ;
;
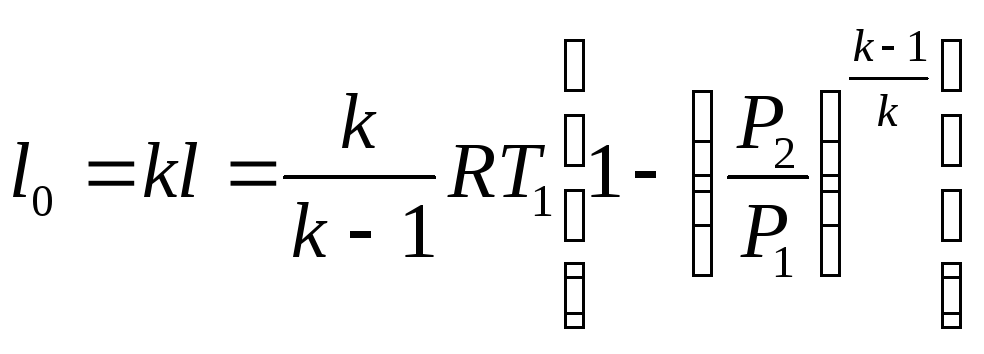
n=k![]()
![]() отсутствует , процесс изоэнтропный.
отсутствует , процесс изоэнтропный.
Закон теплообмена излучением
З-ны описыв-щие излучение абсолютно черного тела с соотв. Поправками исп-ся для получения расч. фор-л теплообмена излучением м\у реальными телами.
ЗАКОН ПЛАНКА
Уст-ет зависимость
спектр. плотности потока излуч. абс.
черн. тела
![]() от длины волны
от длины волны
![]() и температуры Т.
и температуры Т.
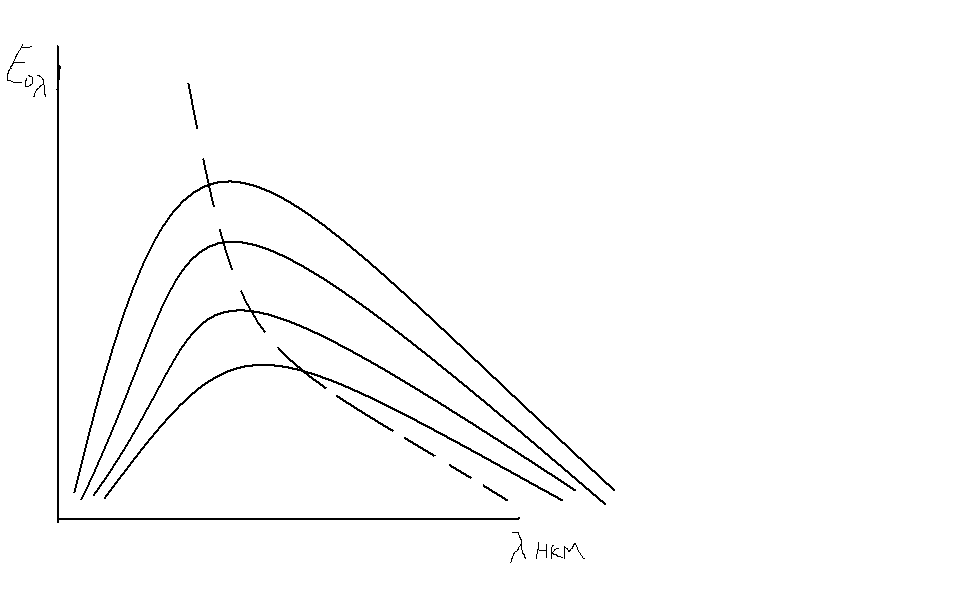
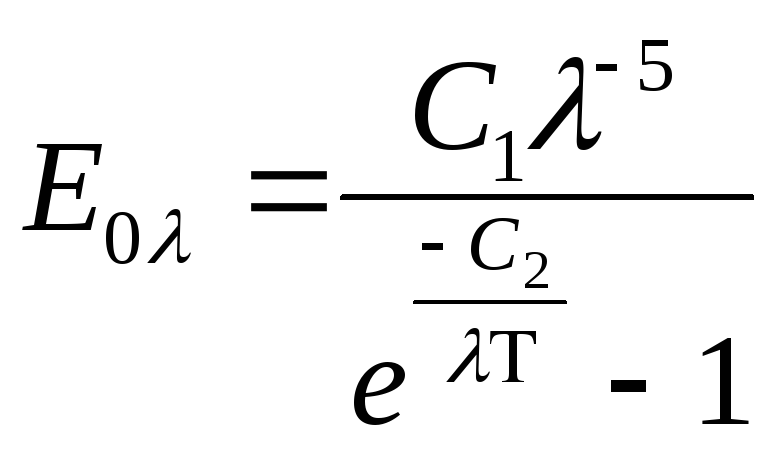 (Вт\м^2*мкм)
(Вт\м^2*мкм)
![]() контакты
контакты
Абс.черн.тело
имеет сплошной спектр излучения, т.е.
излучает при всех длинах волн. Реальные
тела могут иметь сплошной(диэлектрики)и
линейчатый спектры(газы).Сопоставив
зависимости
![]() и
и
![]() для абс.черн. и реального тела, получим
картинку где - - - --абс.черн тело,
_____-реальное
для абс.черн. и реального тела, получим
картинку где - - - --абс.черн тело,
_____-реальное
Способность тела излучать энергию хар-ет спекртальная степень черноты тела

![]() (1)
и
(1)
и
Степень черноты
тела
![]() (2)
(2)
Е-излучательная
способность.Если величина
![]() имеет
одинаковые значения для всех длин волн
и температур,то тело наз-ся серым
имеет
одинаковые значения для всех длин волн
и температур,то тело наз-ся серым
![]() (3)
из (1) с учетом (2) и (3) определим при
(3)
из (1) с учетом (2) и (3) определим при
![]() (для
серого тела)
(для
серого тела)
![]() ;
;
![]() ;
;
![]() (4)
(4)
Для реальных тел,
при различных длинах волн
![]() не
одинакова.
не
одинакова.
ЗАКОН СМЕЩЕНИЯ ВИНА
Макс. Положение в
спектр. Плотности потока излучения
зависит от Т.Длина волн
![]() ,отвечающая макс. Плотности излуч-я
связана с тизлучающего телаур-ем:
,отвечающая макс. Плотности излуч-я
связана с тизлучающего телаур-ем:
![]() мм*К,
где
мм*К,
где
![]() в мм.
в мм.
ЗАКОНЕ СТЕФАНА-БОЛЬЦМАНА
Опред-ет связь
повер-тной плотности потока
излучение,абс.черн.тела
![]() с тем-рой. Это выр-е получ-ся интегрир-ем
закона Планка:
с тем-рой. Это выр-е получ-ся интегрир-ем
закона Планка:
![]() -
коэ-т излуч-я абс.черн.тела
-
коэ-т излуч-я абс.черн.тела
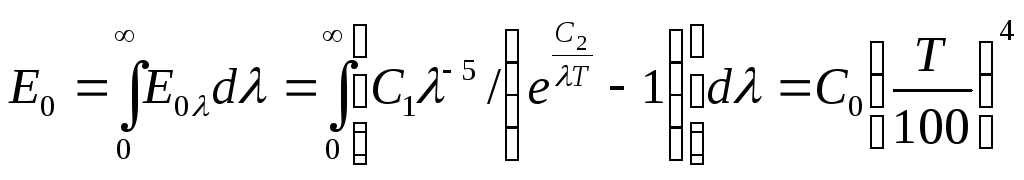
![]() =5,67
Вт\(м^2*K^4)
=5,67
Вт\(м^2*K^4)
Таким образом
получаем:
![]() ;
;
![]() -коэ-т
излучения реального тела.
-коэ-т
излучения реального тела.
ЗАКОН КИРХГОФА
Устан-ет связь м\у спос-ми тела излучать и поглощать энергию ищлучения.Для тел,нах-ся в тепловом равновесии,пов-ная плотность потока и поглащ-ная спос-ть связаны м\у собой.
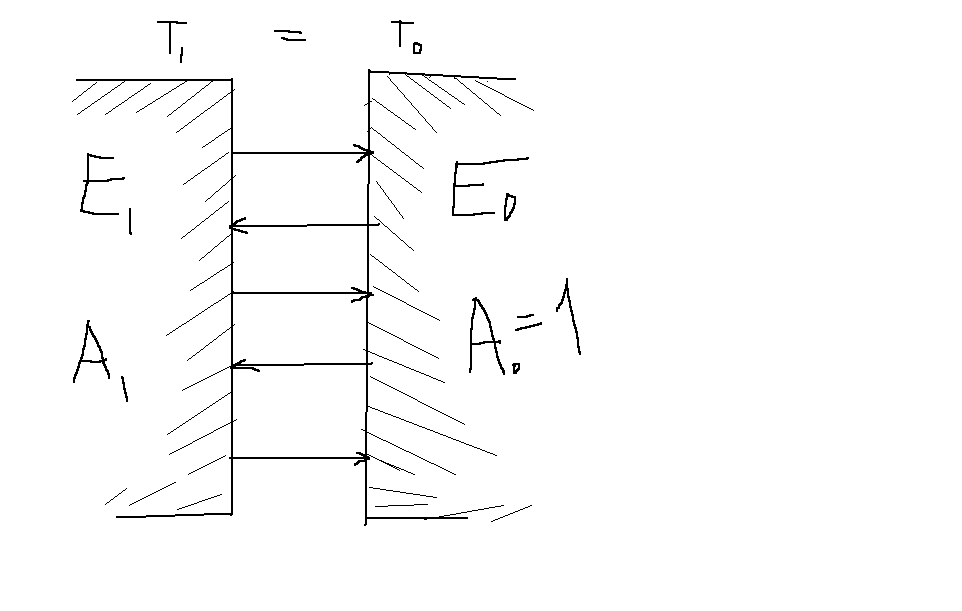 Пусть
одна из рядом расположенных парал-ных
пластин-произвольное тело (
Пусть
одна из рядом расположенных парал-ных
пластин-произвольное тело (![]() ),а
вторая-абс.черн.тело(
),а
вторая-абс.черн.тело(![]() =1)
при равных Т.первая стенка одним кв.
метром погл-ет энергию
=1)
при равных Т.первая стенка одним кв.
метром погл-ет энергию![]() ,а
ее излуч-е и отраж-е полностью поглоща-ся
абс.черн.стенкой,из усл-я тепл-ти
следует
,а
ее излуч-е и отраж-е полностью поглоща-ся
абс.черн.стенкой,из усл-я тепл-ти
следует![]() Это
выр-е справедливо для люб-ой др. стенки
(5)отнощение пов-тной плотности потока
излучения тела к его поглащ-ной спос-ти
одиноково для всех тел,нах-ся при одной
темп-ре и равно пов-ной плотности потока
излучения абс.черн.тела при тойжеТ .из
закона следует,чтот чем больше
поглощает,тем дольше и излучает
тело,поэтому абс.черн.тело имеет
наиб.поверх-ную плотность потока
излучения.Если в
Это
выр-е справедливо для люб-ой др. стенки
(5)отнощение пов-тной плотности потока
излучения тела к его поглащ-ной спос-ти
одиноково для всех тел,нах-ся при одной
темп-ре и равно пов-ной плотности потока
излучения абс.черн.тела при тойжеТ .из
закона следует,чтот чем больше
поглощает,тем дольше и излучает
тело,поэтому абс.черн.тело имеет
наиб.поверх-ную плотность потока
излучения.Если в![]() (5) величину Е выразиь ч\з степень черноты
по зак-у СТЕФ-БОЛЬЦ,то Ур-ние примит вид
(5) величину Е выразиь ч\з степень черноты
по зак-у СТЕФ-БОЛЬЦ,то Ур-ние примит вид![]() следут, что
следут, что![]() Закон КиРТ-ФА справедлив и для спектр.
Излучения,для опред. Длины волн примит
вид
Закон КиРТ-ФА справедлив и для спектр.
Излучения,для опред. Длины волн примит
вид
![]()
ТЕПЛООБМЕН ИЗЛУЧЕНИЯ М\У ТВЕРДЫМИ ТЕЛАМИ РАЗДЕЛЕННЫМИ ГЕОТЕРМИЧНОЙ СРЕДОЙ
1ый СЛУЧАЙ
Излучение м\у 2мя парал-ми стенками
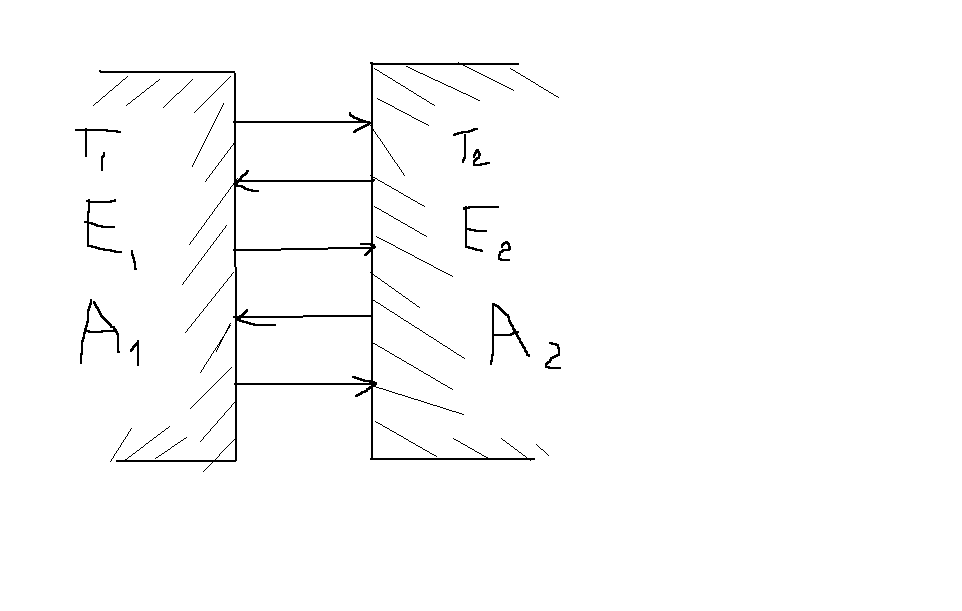
2 стенки,с большими
пов-ями и стоят на небольшом
расстоянии,так,что излучение каждой
стенки полностью попадает на
противоположную,частично отражаясь и
поглощаясь,что имеет затухающий
хар-р.Обозначим
![]() плотность
потока эф-ного излучения от 1ой стенки
ко 2ой,аналогично и
плотность
потока эф-ного излучения от 1ой стенки
ко 2ой,аналогично и![]() .Величины
равны:
.Величины
равны:
![]()
![]() ,где
,где
![]() - потоки излучения
стенок 1и2
- потоки излучения
стенок 1и2
![]() -поток отражений стенок 1и2
-поток отражений стенок 1и2
![]() -коэф-т отраженной
-коэф-т отраженной
![]() той
стенки подставив
той
стенки подставив![]() и
и![]() получим
получим
![]() и
и
![]() найдем
результ-щий поток
найдем
результ-щий поток![]() используя
полученные ранее формулы получаем
используя
полученные ранее формулы получаем
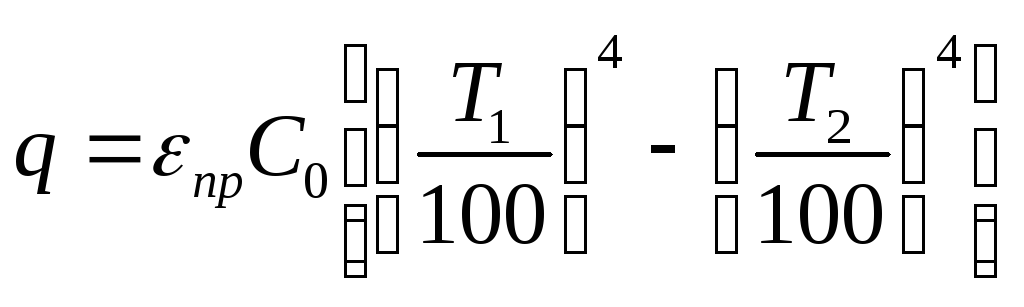 ,где
,где
![]() приведенная
степень черноты сис-мы сост-щей из 2х
стенок
приведенная
степень черноты сис-мы сост-щей из 2х
стенок