
- •1 Закон тд для закр. Неподвиж. Сис-мы.
- •1Ый з-н термодинамики для закрытой подвижной системы
- •I з-н тд для открытой системы(стационарного поточного процесса.
- •2Ой з-н термодинамики:
- •Круговые проц или Циклы :
- •Дросселирование газов
- •Необратимые термодинамические процессы
- •Обратимые и необрат процессы
- •ПОлитропные процессы ид.Газа
- •Термич.Поле. Градиент температуры.
- •Механизмы и законы переноса теплоты. Явление теплопроводности, теплоотдачи и излучения.
- •Тепловая хар-ка обратимых циклов.
- •Теплообмен излучением
- •Основные понятия ти
- •Законы теплообмена излучения.
- •1.Физ. Условия теплообмена конвекцией.
- •2,Факторы, определяющие интенсивность конвективного теплообмена.
- •Теплоптоводность ч/з многослойную цил-ую стенку.
- •Теплоптоводность ч/з цил-ую стенку.
- •Цикл Карно (цк). Теорема Карно.
- •2Ой случай
- •3Ий случай
- •Цикл Отто.
- •Цикл Дизеля.
- •Теплопередача через многослойную цилиндрическую стенку.
- •Критический диаметр тепловой изоляции трубопровода.
- •Факторы определяющие интенсивность конвективного теплообмена.
- •Числа подобия процессов конвективного теплообмена.
Теплоптоводность ч/з многослойную цил-ую стенку.
t λ1 λ2………… λn


















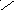












 tw1
t1w2
tw1
t1w2
t1w3
t11w2
t11w3
t11w4 twn+1
r1
r
r2
rn+1
Получим ф-лу для опред-ия теплового потока ч/з многослойную цил-ую стенку сост-ую из n слоёв с учётом контактного термич-го сопротивления м/у слоями. На границах стенки заданы ГУ 1-го рода.
при r=r1 , t=tw1
при r=rn+1 , t=twn+1
Величины qe (нижний коэф-ент не понятен,то-ли l то-ли e!!!) для i-го слоя и i-ой пов-ти контакта равны:
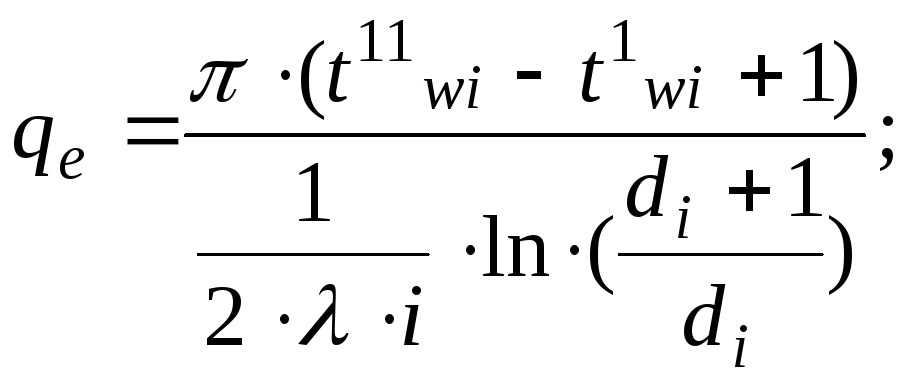
![]()
Записав эти потоки для каждого из n слоёв и n-1-ой пов-ти контакта и исключив после этого промеж-ые t-ры получим:
![]() (1)
(1)
t-ры пов-ти стенки определим также как и в случае плоской стенки на ПР:
t1w3
из (1)
t1w3=tw1-![]()
Теплоптоводность ч/з цил-ую стенку.

На границах стенки заданы ГУ 1-го рода.
при r=r1 , t=tw1 при r=r2 , t=tw2
в этом случае тепловой поток имеет радиальное направление, темпер. поле одномерно. для стационар. одномер. задачи о теплопро-ти цил. стенки дифур-ие (1.5) в цил-й системе коорд-т при λ=const примет
![]() (1.14)
(1.14)
введя новую
переменную г=![]() ,
преобр-ем (1.14)
,
преобр-ем (1.14)
![]()
после раздел-я перем-х и интегр-я получим lnu + lnr = lnC1 (1.15)
потенцируя получим u*r= C1
перейдя к первонач
переем-м, запишем
![]() r
r![]() =C1
, а затем разделив получаем
=C1
, а затем разделив получаем
t= C1lnr+ C2 (1.16)
искривление линии
темпер-го поля в цил-ой стенке обуслов-о
изменением плотности тепл-го потока
q=![]() при изменении радиуса цилиндра. при
увеличенииr
величина площади F=2πrl,
где l
– длина стенки, также увел-ся. поэтому
на больших r
темп-ая линия проходит более полого и
наоборот. Это правило сохр-ся и при
обратном направ-ии тепл. потока(пунктир
на рис.).
при изменении радиуса цилиндра. при
увеличенииr
величина площади F=2πrl,
где l
– длина стенки, также увел-ся. поэтому
на больших r
темп-ая линия проходит более полого и
наоборот. Это правило сохр-ся и при
обратном направ-ии тепл. потока(пунктир
на рис.).
Подставив ГУ в (1.16) найдем C1 и C2 :
C1=![]() C2
=
C2
=
![]() (1.18)
(1.18)
преобр-м 1.16 с учетом
1.18 :
![]() (1.19)
(1.19)
г деd1
и d2
– внутр и наруж диам-ы цилиндра, d
– текущ-й диам-р цил-ра.
деd1
и d2
– внутр и наруж диам-ы цилиндра, d
– текущ-й диам-р цил-ра.
из (1.19) опред-им
темпер-й градиент:
![]() =
=![]() (1.20)
(1.20)
использ (1.20) найдем
тепл-й поток ч/з стенку: Q=qF=-λ![]() 2πrl=
2πrl= (1.21)
(1.21)
тепловой поток на
единицу длины
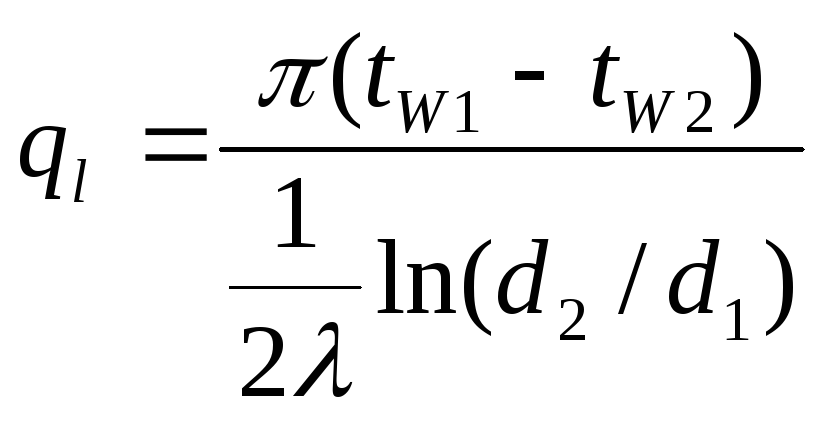 (1.22)
(1.22)
величину
![]() назыв
внутр термич сопр-ем цил стенки.обозначим
плотности тепл. потока на внутр и внеш
поверх-ях ч/з
назыв
внутр термич сопр-ем цил стенки.обозначим
плотности тепл. потока на внутр и внеш
поверх-ях ч/з![]() и
и![]() . т.к.Q=
. т.к.Q=![]() l=
l=![]() π
π![]() l=
l=![]() π
π![]() l
l
![]() =
=![]() π
π![]() =
=![]() π
π![]() (1.23)
(1.23)
![]()
![]()
Истечение и дросселирование газов.
Общее уравнение истечения газов.
П ри
скоростиw2
в выходном сечении канала частица
жидкости или газа перемещаться за время
dτ
на расстояние dx=w2dτ
в результате ч/з сечение -2- за время dτ
пройдет масса dm=ρ2F2dx
в единицу времени масса будет равна.
ри
скоростиw2
в выходном сечении канала частица
жидкости или газа перемещаться за время
dτ
на расстояние dx=w2dτ
в результате ч/з сечение -2- за время dτ
пройдет масса dm=ρ2F2dx
в единицу времени масса будет равна.
G=ρ2w2F2 при стационарном течении расход газа ч/з любое сечение канала будет один и тот же в этом случае уравнение расхода или уравнении неразрывности будет иметь вид первого закона термодинамики для стационарного потока был получен ранее пренебрегая для газа изменением потенциальной энергии g(z2-z1) запишем этот закон в следующем виде
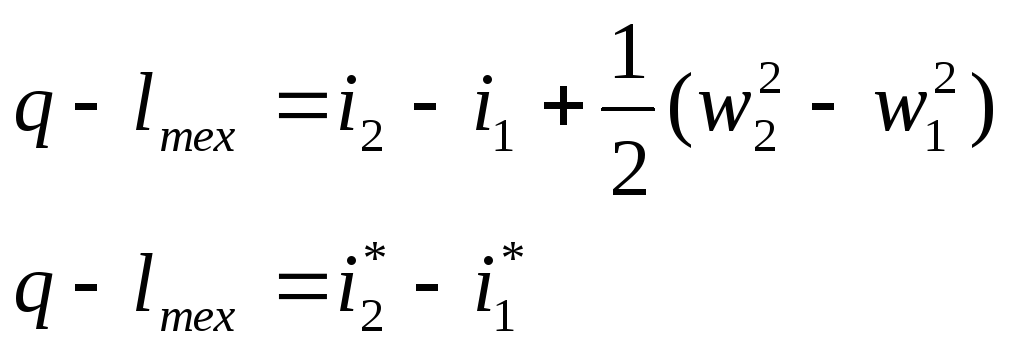 (3.2)
где
(3.2)
где
![]()
T* - температура торможения
В дифференциальном виде уравнения (3.2) примут вид
 (3.3)
(3.3)
Сопоставив (3.3) с
ф-ой (![]() )
получим уравнение энергии в другом виде
)
получим уравнение энергии в другом виде
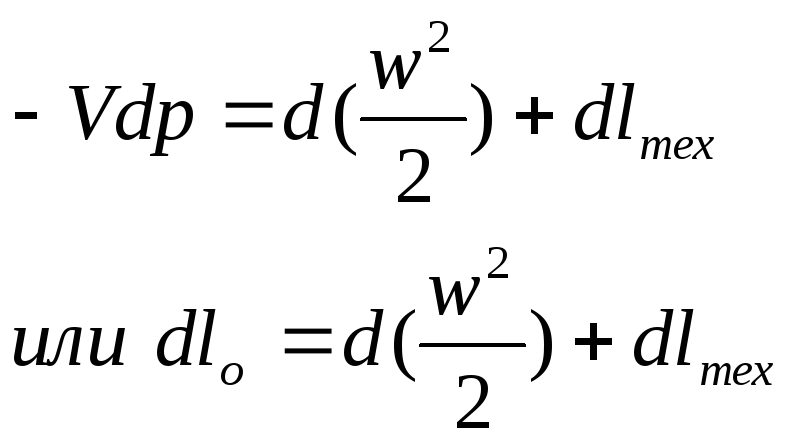 (3.4)
(3.4)
В конечном виде уравнение энергии запишется следующим образом
![]()
В качестве 3-го уравнения при расчете истечения газа используют уравнения состояния
pV=RT или p=ρRT (3.6)
Истечение идеального газа.
q=0 и lтех =0 в произвольном канале из (3.2) найдем
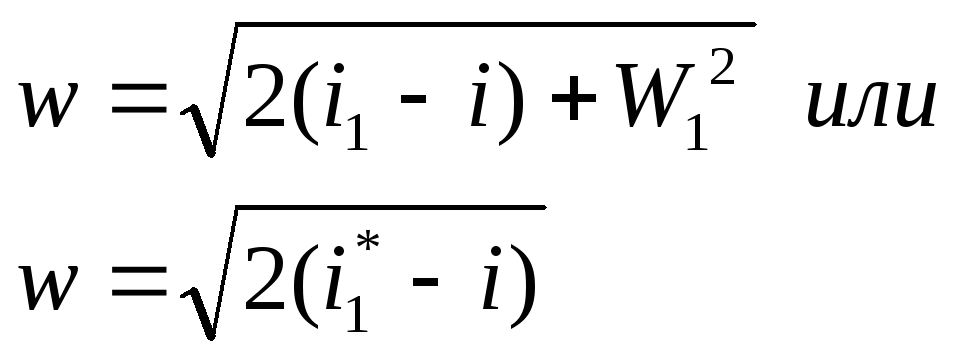 (3.7)
(3.7)
где w2=w – конечное значение скорости.
Это уравнение справедливо для идеального и реального газов для идеального газа используются pV=RT или p=ρRT (3.6) и pVk=const, TVk-1=const, Tk=pk-1const (2.33) получим
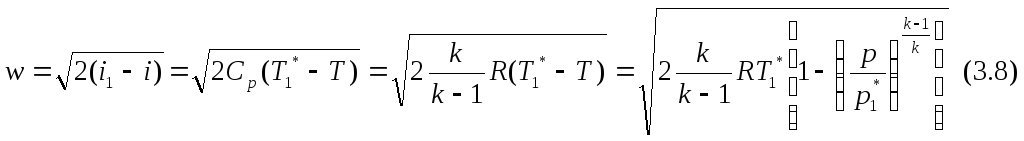
Расход газа будет равен
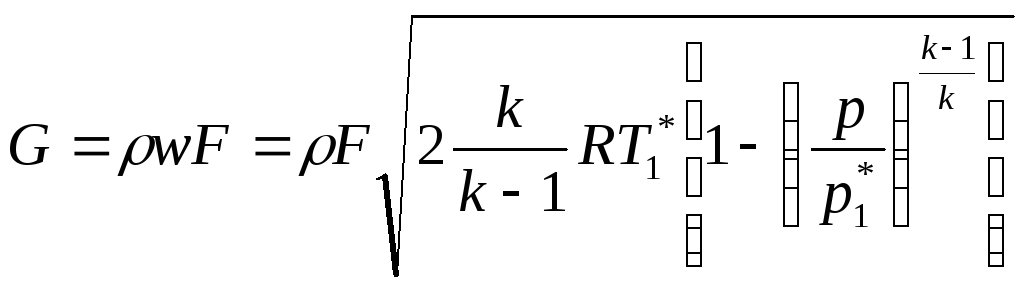 (3.9) где
(3.9) где
![]() ;
;
p*- полное давление, давление торможения
P*=const P=const
*
![]()
Для получения однозначного значения полного движения принято считать, что торможение потока происходит по изоинтропе, в этом случае так же справедливо уравнение Клапейрона
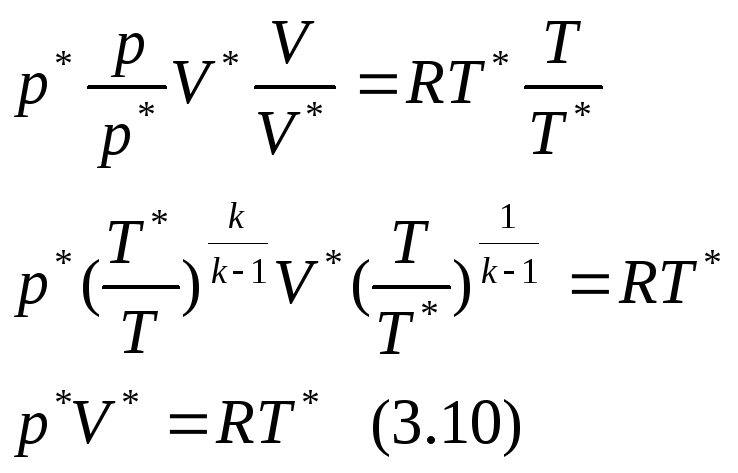
Скорость звука.
Из физики известна ф-ла для определения скорости распределения возмущений в сплошной среде которая совпадает с местной скоростью звука
![]() (3.11)
(3.11)
При адиабатном процессе давление связано с плотностью следующим образом:
PVk=const;
pρ-k=const;
p=ρkconst ![]()
Подставив (3.12) в (3.11) получим уравнение для определения местной скорости звука в потоке газа
![]()
Скорость газа часто определяют с помощью числа маха
Мах
![]() (3.14)
(3.14)
При М<1 - до
М=1 - звуковой
М>1 - сверх
