Решение:
Цикл
Карно состоит из двух изотерм
(изотермического расширения ![]() при
температуре
при
температуре ![]() и
изотермического сжатия
и
изотермического сжатия ![]() при
температуре
при
температуре ![]() ) и
двух адиабат (адиабатического
расширения
) и
двух адиабат (адиабатического
расширения ![]() и
адиабатического сжатия
и
адиабатического сжатия ![]() ).
При адиабатическом расширении
и
адиабатическом сжатии
теплообмен
с окружающей средой отсутствует, и
поэтому работы расширения
и
сжатия
совершаются
за счет изменения внутренней энергии
).
При адиабатическом расширении
и
адиабатическом сжатии
теплообмен
с окружающей средой отсутствует, и
поэтому работы расширения
и
сжатия
совершаются
за счет изменения внутренней энергии ![]() и
и ![]() .
Следовательно,
работы
газа в адиабатических процессах
и
.
Следовательно,
работы
газа в адиабатических процессах
и ![]() равны
по величине:
равны
по величине: ![]() ,
а на
-диаграмме
графически определяются
площадями
,
а на
-диаграмме
графически определяются
площадями ![]() и
и ![]() заштрихованных
фигур под графиками соответствующих
процессов, и эти площади равны
заштрихованных
фигур под графиками соответствующих
процессов, и эти площади равны ![]() .
.
Задание N 2. |
Средняя кинетическая энергия молекул газа при температуре зависит от их конфигурации и структуры, что связано с возможностью различных видов движения атомов в молекуле и самой молекулы. При условии, что имеет место только поступательное и вращательное движение молекулы как целого, средняя кинетическая энергия молекул азота равна … |
Решение:
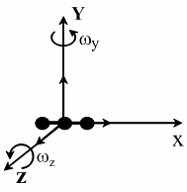
Для статистической системы в состоянии термодинамического равновесия на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная , а на каждую колебательную степень – . Средняя кинетическая энергия молекулы равна , где – сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы молекулы. При условии, что имеют место только поступательное и вращательное движение, сумма числа степеней свободы равна ; где – число степеней свободы поступательного движения, равное ; – число степеней свободы вращательного движения, которое может быть равно . Для молекулярного азота (двухатомной молекулы) и . Следовательно, (3 степени свободы поступательного движения по направлениям осей ординат и 2 степени свободы вращательного движения вокруг осей и ) (см. рис.). Тогда средняя энергия молекул азота равна .
Задание N 2. |
Если
не учитывать колебательные движения
в линейной молекуле углекислого
газа |
Ешение:
Средняя
кинетическая энергия молекулы равна ![]() ,
где
,
где ![]() –
постоянная Больцмана,
–
термодинамическая температура,
–
сумма числа поступательных, числа
вращательных и удвоенного числа
колебательных степеней свободы
молекулы:
.
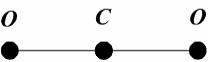
Для
линейной молекулы углекислого газа
(см.
рис.) число степеней свободы поступательного
движения
,
вращательного –
,
колебательного –
–
постоянная Больцмана,
–
термодинамическая температура,
–
сумма числа поступательных, числа
вращательных и удвоенного числа
колебательных степеней свободы
молекулы:
.
Для
линейной молекулы углекислого газа
(см.
рис.) число степеней свободы поступательного
движения
,
вращательного –
,
колебательного – ![]() ,
поэтому
,
поэтому ![]() .
.
 Следовательно,
средняя кинетическая энергия
молекулы
равна
Следовательно,
средняя кинетическая энергия
молекулы
равна ![]() .
Средняя
энергия вращательного движения
.
Средняя
энергия вращательного движения ![]() и
составляет
и
составляет 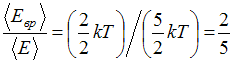 части
от полной энергии.
части
от полной энергии.