Задача №1
На
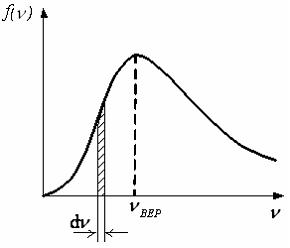
рисунке представлен график функции
распределения молекул идеального газа
по скоростям (распределение Максвелла),
где ![]() –
доля молекул, скорости которых заключены
в интервале скоростей от
–
доля молекул, скорости которых заключены
в интервале скоростей от ![]() до
до ![]() в
расчете на единицу этого интервала.
в
расчете на единицу этого интервала.
 Для
этой функции является верным утверждение,
что …
Для
этой функции является верным утверждение,
что …
Ответ:при изменении температуры площадь под кривой не изменяется
Задание N 2. |
Молярная
теплоемкость идеального газа при
постоянном давлении равна |
Решение:
Молярные
теплоемкости ![]() и
и ![]() в
изохорном и изобарном процессах
соответственно равны:
в
изохорном и изобарном процессах
соответственно равны: ![]() и
и ![]() .
Сравним:
.
Сравним: 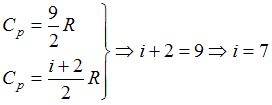 .
Сумма
числа степеней свободы
.
Сумма
числа степеней свободы ![]() может
быть представлена как
может
быть представлена как ![]() ;
где
;
где ![]() число
степеней свободы поступательного
движения
число
степеней свободы поступательного
движения ![]() ;
; ![]() число
степеней свободы вращательного движения,
которое может быть равно
число
степеней свободы вращательного движения,
которое может быть равно ![]() ;
; ![]() –
число степеней свободы колебательного
движения, минимальное количество которых
равно 1 (см. рис.).
–
число степеней свободы колебательного
движения, минимальное количество которых
равно 1 (см. рис.).
 Следовательно,
Следовательно, ![]() и
и
![]() .
.
Задание N 3. |
Чтобы
расплавить некоторую массу меди,
требуется большее количество теплоты,
чем для плавления такой же массы цинка,
так как удельная теплота плавления
меди в 1,5 раза больше, чем цинка ( |
Решение:
В
термодинамике изменение энтропии
определяется формулой ![]() ,
где
,
где ![]() –
количество теплоты, полученное системой
при температуре
–
количество теплоты, полученное системой
при температуре ![]() .
Пусть изменение энтропии при плавлении
цинка
.
Пусть изменение энтропии при плавлении
цинка 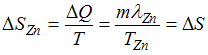 ,
тогда энтропия меди при ее плавлении
возрастет на
,
тогда энтропия меди при ее плавлении
возрастет на 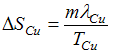 .
Найдем отношение
.
Найдем отношение 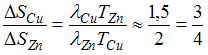 .
Следовательно,
.
Следовательно, ![]() .
.
Задание N 4. |
||
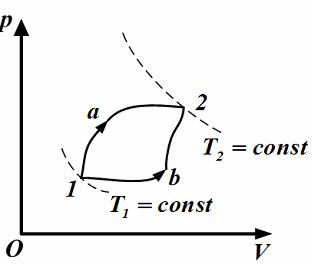
Идеальный
газ переводится из первого состояния
во второе двумя способами (
|
Решение:
При
любом способе перехода идеального газа
из первого состояния во второе, согласно
первому началу термодинамики, теплота,
сообщаемая газу, расходуется на изменение
его внутренней энергии и на совершение
им работы против внешних сил: ![]() .
При этом изменение внутренней энергии,
как однозначной функции термодинамического
состояния системы,
.
При этом изменение внутренней энергии,
как однозначной функции термодинамического
состояния системы, ![]() не
зависит от способа перехода и определяется
только разностью значений внутренней
энергии этих состояний:
не
зависит от способа перехода и определяется
только разностью значений внутренней
энергии этих состояний: ![]() .
Работа
.
Работа 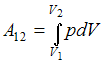 ,
совершаемая газом при изменение его
объема от
,
совершаемая газом при изменение его
объема от ![]() до
до ![]() ,
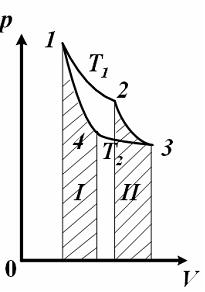
зависит от процесса перехода. Величина
этой работы равна площади фигуры под
графиком процесса в координатных
осях
,
зависит от процесса перехода. Величина
этой работы равна площади фигуры под
графиком процесса в координатных
осях ![]() (см.
рис.).
(см.
рис.).
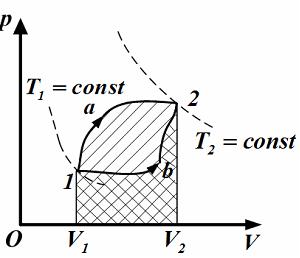
![]() ,
так как площади заштрихованных фигур
,
так как площади заштрихованных фигур ![]() .
Следовательно, по первому закону
термодинамики:
.
Следовательно, по первому закону
термодинамики: ![]() .
Теплота,
полученная газом, изменение внутренней
энергии и работа газа при переходе его
из одного состояния в другое связаны
соотношениями:
.
Теплота,
полученная газом, изменение внутренней
энергии и работа газа при переходе его
из одного состояния в другое связаны
соотношениями: ![]() .
.
Задание N 1. |
Зависимость
давления идеального газа во внешнем
однородном поле силы тяжести от высоты
для двух разных температур ( |

 Для
величины работы адиабатического
расширения газа
Для
величины работы адиабатического
расширения газа