§ 6. Исследование теоретико-игровой модели
Теорема. Справедливы следующие утверждения.
1. Множество стратегий 1-го игрока
в игре
не
пусто тогда и только тогда, когда
выполняются неравенства (4.27).
2. Если одно из неравенств (4.27) выполняется как равенство, то множество стратегий 1-го игрока в игре содержит только одну стратегию, которая, очевидно, является доминирующей стратегией 1-го игрока. В частности, если как равенство выполняется левое из неравенств (4.27), то этой стратегией является функция
,
, (6.1)
если же как равенство выполняется правое из неравенств (4.27), то этой стратегией является функция
,
. (6.2)
3. Если оба неравенства (4.27) выполняются
как строгие, то функция
,
значения которой находятся по формулам
(5.19), (5.20), является доминирующей стратегией
1-го игрока в игре
.
Доказательство. Множество стратегий 1-го игрока в игре по определению совпадает с множеством решений краевой задачи (4.7) – (4.10). Поэтому справедливость первого утверждения теоремы вытекает из леммы 2.
Далее, с учетом определения игры , связи между неравенствами (4.25) и (4.27), а также связи между задачами (4.16) – (4.20) и (4.6) – (4.10) второе утверждение теоремы является прямым следствием замечания 1.
Докажем основное, третье утверждение теоремы. По определению доминирующей стратегии нужно доказать, что
, (6.3)
,
,
где, напомним,
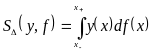, (6.4)
т.е. нужно доказать, что решением задачи
на максимум функционала (4.1) при
ограничениях (4.2) – (4.4) вне зависимости
от выбора функции
является функция
.
Ранее (лемма 4) это было доказано при
дополнительном предположении, что
рассматриваемые функции
при
почти всех
имеют положительную производную
.
Откажемся теперь от этого предположения.
Выберем произвольную функцию
и произвольную функцию
и покажем, что для них и для функции
справедливо неравенство (6.3), которое с
учетом формулы (6.4) имеет вид
. (6.5)
Из определения множества
следует, что всякая функция
является неубывающей на интервале
.
Поэтому в силу известных свойств
интеграла неравенство (6.5) будет доказано,
если будет доказано, что
,
. (6.6)
В свою очередь, неравенство (6.6) будет доказано, если будет доказано, что
,
, (6.7)
где
,
есть решения краевой задачи (4.16) –
(4.20), причем первое из них соответствует
оптимальному управлению
,
а второе — некоторому допустимому
управлению
.
По формуле (4.21) эти решения можно
представить в виде
, (6.8)
. (6.9)
Поскольку является допустимым управлением в задаче (4.16) – (4.20), то, в частности,
при почти всех
.
В то же время, согласно формуле (5.12),
,
.
Поэтому из (6.8) и (6.9) следует, что
,
. (6.10)
Таким образом, для доказательства неравенства (6.6) остается показать, что
,
. (6.11)
Для доказательства этого неравенства
заметим, что функции
и
как решение краевой задачи (4.17) – (4.20)
можно также представить в виде
,
, (6.12)
,
. (6.13)
Так как управление является допустимым в задаче (4.16) – (4.20), то, в частности,
при почти всех
.
В то же время, согласно формуле (5.12),
,
.
Поэтому из формул (6.12) и (6.13) с учетом
того, что в них
,
получим неравенство (6.11). Теорема
доказана.
В заключение, возвращаясь к нашей
исходной задаче построения шкалы ставок
налога, отметим, что доказанная теорема
позволяет считать функцию
,
определяемую по формуле (2.1.22) оптимальной
модельной шкалой. Точнее, если оба
неравенства (4.27) выполняются как строгие,
то оптимальной модельной шкалой ставок
подоходного налога является функция
(2.1.18)
где (2.1.19)
.
В свою очередь, если левое из неравенств (4.27) выполняется как равенство, то оптимальной модельной шкалой ставок подоходного налога является функция
(2.1.18А)
Наконец, если как равенство выполняется правое из неравенств (4.27), то оптимальной модельной шкалой ставок подоходного налога является функция
(2.1.18В)
1
Выше негласно предполагалось, что
множество
,
как и множество
,
непусто.