Здесь представлено доказательство из пособия:

Чистяков С.В., Ишханова М.В. Математические модели выбора налоговых шкал. СПб., 1998.

Естественно, что нумерация формул другая. Я только исправил те номера, где ссылка на формулы из моей книги. Кроме того, в приводимом фрагменте пособия функция выигрыша обозначена не через T, а через S.

Р.О. Смирнов.

Сергей Владимирович Чистяков,

Марина Владимировна Ишханова

МАТЕМАТИЧЕСКИЕ МОДЕЛИ ВЫБОРА НАЛОГОВЫХ ШКАЛ

Учебное пособие

Зав. редакцией Г.Чередниченко

Редактор Ф. Бастиан

Техн. редактор Л.Иванова

Лицензия ЛР № 040050 от 15.08.96.

Подписано в печать с оригинала-макета 17.06.98. Ф-т 60  84 / 16.

Печать офсетная. Усл.печ.л. 3,02. Уч.-изд. л. 2,85.

Тираж 200 экз. Заказ №

Редакция оперативной подготовки

учебно-методических и научных изданий

Издательства Санкт-Петербургского университета.

199034, С.-Петербург, Университетская наб., 7/ 9.

Центр оперативной полиграфии

Санкт-петербургского университета.

199034, С.-Петербург, наб. Макарова, 6 .

Литература

1. Инструкция № 35 по применению закона Российской Федерации о подоходном налоге с физических лиц с изменениями и дополнениями. М.: Изд-во “Ось-89”, 1995. 96 с.

2. Your Federal Income Tax. Publication 17. IRS, 1990.

3. Львов Ю.А. Основы экономики и организации бизнеса. СПб.: ГМП “Формика”, 1992. 383 с.

4. Смирнов Р.О., Чистяков С.В. О ставках налогообложения как инструменте государственного регулирования // Экономика и мат. методы. 1993. Т.29. Вып.2. С. 268–274.

5. Филиппов А.Ф. Дифференциальные уравнения с разрывной правой частью. М.: Наука, 1985. 224 с.

6. Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Математическая теория оптимальных процессов. М.:Наука, 1969. 392 с.

7. Рудин У. Основы математического анализа. М.: Мир, 1976. 319 c.

8. Зангвил У.И. Нелинейное программирование: Единый подход: Пер.с англ. М.: Сов. радио, 1973. 312 с.

9. Пшеничный Б.Н., Данилин Ю.М. Численные методы в экстремальных задачах. М.: Наука, 1975. 96 с.

Оглавление

Литература 4

§ 5. Решение вспомогательной задачи оптимального управления 11

§ 6. Исследование теоретико-игровой модели 17

С целью доказательства того, что в игре Г существует доминирующая стратегия 1-го игрока, запишем формулу (2.1.14) с учетом условий (2.1.17) в следующем виде:

, (2.1.21)

где .

Теперь рассмотрим “усеченную” антагонистическую игру , в которой множество стратегий 1-го (2-го) игрока совпадает с множеством всех функций, каждая их которых представляет собой сужение на промежуток той или иной функции , а функция выигрыша имеет вид

, .

Из определения игр и следует, что если будет доказано существование доминирующей стратегии 1-го игрока в игре , то стратегия такая, что

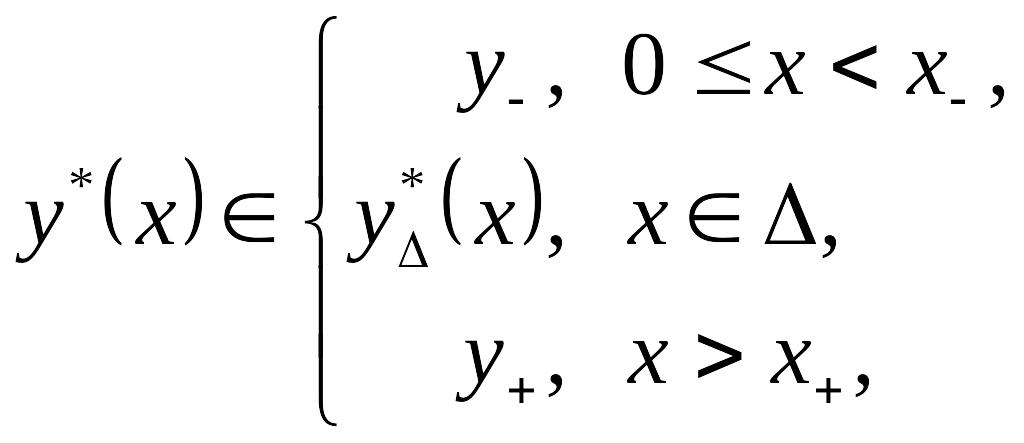(2.1.22)

будет доминирующей стратегией 1-го игрока в игре . Эту стратегию естественно считать оптимальной модельной шкалой средних ставок налога при заданных параметрах , , , , .

Для доказательства существования доминирующей стратегии 1-го игрока в игре зафиксируем произвольную стратегию 2-го игрока и рассмотрим задачу на максимум функционала

, (2.1.23)

где .

Очевидно, что если будет доказано, что задача имеет решение, не зависящее от выбранной функции , то это решение будет доминирующей стратегией 1-го игрока в игре . Докажем это сначала в том случае, когда дифференцируема и имеет при почти всех положительную производную . В этом случае интеграл Стилтьеса сводится к обычному интегралу Римана:

.

Поэтому задача на максимум функционала (2.1.23) при ограничениях (2.1.15) – (2.1.17) равносильна следующей задаче оптимального управления:

, (4.6)

, (4.7)

(4.8)

,

, (4.9)

(4.10)

.

Выясним условия существования допустимого управления в этой задаче, а, следовательно, непустоты множества стратегий 1-го игрока в игре .¹ С этой целью сделаем в задаче (4.6) – (4.10) замену

, (4.11)

, (4.12)

, (4.13)

, (4.14)

. (4.15)

В результате этой замены задача (4.6) – (4.10) примет вид

, (4.16)

, (4.17)

, (4.18)

, (4.19)

(4.20)

.

Очевидно, что если будет установлено условие существования допустимого управления в задаче (4.16) – (4.20), то, пользуясь зависимостями (4.11) – (4.15) между функциями и параметрами этой задачи и функциями и параметрами задачи (4.6) – (4.10), будет установлено и условие существования допустимого управления в задаче (4.6) – (4.10).

Проинтегрируем уравнение (4.17) с начальным условием (4.19) для произвольного допустимого управления . В итоге получим

. (4.21)

Рассмотрим два постоянных управления

,

и, соответственно,

, .

Эти управления могут и не быть допустимыми. По формуле (4.21) найдем соответствующие им решения уравнения (4.17) с начальным условием (4.19)

, (4.22)

. (4.23)

Поскольку предполагается, что при почти всех , то для решений (4.21), (4.22) и (4.23) будет справедливо неравенство

.

Отсюда с учетом формул (4.22) и (4.23) при , получим

. (4.24)

Поэтому если здесь управление является допустимым в задаче (4.16) – (4.20), т.е. если , то должно выполняться неравенство

. (4.25)

Очевидно, верно и обратное, т.е. если справедливо это неравенство, то в задаче (4.16) – (4.20) существует допустимое управление. Действительно, с учетом формул (4.22) и (4.23) неравенство (4.25) может быть переписано в виде

, (4.26)

а это с учетом определения решений и , а также с учетом теоремы о непрерывной зависимости решений дифференциального уравнения от параметров означает, что в задаче (4.16) – (4.20) существует, и при этом постоянное, допустимое управление , .

Таким образом, справедливо следующее утверждение.

Лемма 1. Для того чтобы в задаче (4.16) – (4.20) существовало допустимое управление, необходимо и достаточно, чтобы выполнялись неравенства (4.25).

Замечание 1. Если одно из нестрогих неравенств (4.25) выполняется как равенство, то, как следует из вывода этих неравенств, в задаче (4.16) – (4.20) существует единственное, с точностью до эквивалентности измеримых по Лебегу функций, допустимое управление. А именно этим единственным допустимым управлением будет постоянное управление , если как равенство выполняется левое из неравенств (4.25), и, соответственно, им будет постоянное управление , если как равенство выполняется правое из неравенств (4.25).

Замечание 2. Справедливо и обратное утверждение к утверждению, сформулированному в замечании 1. А именно если одно из постоянных управлений или является допустимым в задаче (4.16) – (4.20), то в первом случае левое из неравенств будет выполняться как равенство, а во втором, соответственно, правое из этих неравенств будет выполняться как равенство. Причем в обоих этих случаях других допустимых управлений, с точностью до эквивалентности измеримых по Лебегу функций, в задаче (4.16) – (4.20) нет.

Замечание 3. Если одно из нестрогих неравенств (4.25) выполняется как равенство, то с учетом замечания 1 одно из указанных в нем управлений и будет оптимальным (в силу единственности допустимого управления). В этом случае оптимальное управление, очевидно, не зависит от выбранной ранее функции .

В силу имеющихся связей (4.11) – (4.15) между задачами (4.6) – (4.10) и (4.16) – (4.20) из леммы 1 в качестве следствия получим следующее утверждение.

Лемма 2. Для того чтобы в задаче (4.6) – (4.10) существовало допустимое управление, необходимо и достаточно, чтобы выполнялось следующее неравенство:

. (4.27)

Значение этого условия в конечном итоге состоит в том, что оно позволяет проверить, корректно ли поставлена исходная задача о построении оптимальной налоговой шкалы. В частности, если для выбранных каким-то образом параметров , , , , неравенство (4.27) не выполняется, то необходимо скорректировать выбор всех или некоторых из этих параметров.