7.6. Обчислення невласних інтегралів в середовищі Maxima

У символьному режимі (аналітично) невласні інтеграли з нескінченними границями інтегрування обчислюються, якщо в параметрах команди integrate вказувати, наприклад, x, 0, inf.

Приклади. Обчислити невласні інтеграли

1)

(%i2) integrate(1/(x*sqrt(1+x^2)),x,1/2,inf);

(%o2) asinh(2)

(%i3) float(%), numer;

(%o3) 1.44363547517881

2)

(%i4) integrate(1/(x^2+6*x+12),x,-inf,inf);

(%o4) %pi/sqrt(3)

(%i5) float(%), numer;

(%o5) 1.813799364234218

Чисельне інтегрування виконується функцією romberg або за допомогою функцій пакету quadpack.

Приклади. 1) Обчислити невласний інтеграл .

Необхідно скористатися рядком меню основного вікна Maxima і вибрати розділ Аналіз → Integrate…

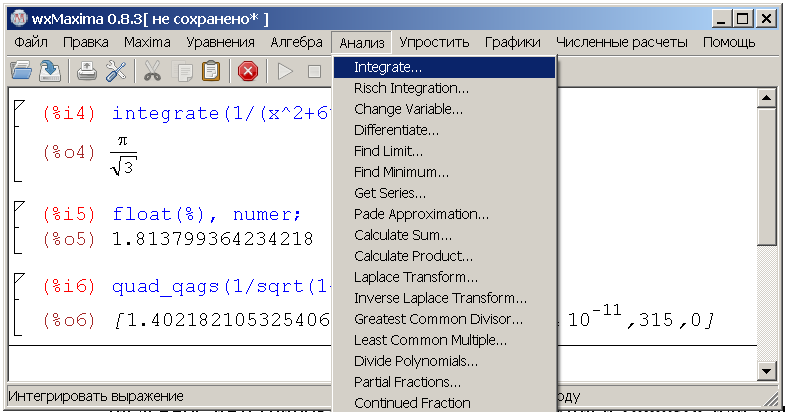
Виникає допоміжне вікно Інтегрувати, в якому вводиться підінтегральна функція, границі інтегрування визначного інтеграла і чисельне інтегрування за допомогою функції romberg або функцій пакету quadpack.

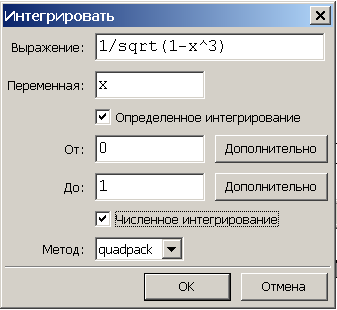
Натискує клавішу Ok, в робочому вікні виникає результат розрахунку

(%i6) quad_qags(1/sqrt(1-x^3), x, 0, 1);

(%o6) [1.402182105325406,9.8784758151282404*10^-11,315,0]

2) Обчислити невласний інтеграл .

Аналогічно попередньому прикладу, отримуємо наступний результат:

(%i8) quad_qagi(x*exp(-х)*sqrt(1-exp(-х)), x, 0, inf);

(%o8) [0.85358153702822,6.8297022008283337*10^-9,255,0]

Приклади для самостійного розв‘язання

Обчислити невласні інтеграли:

1) . 2) . 3) . 4) .

5) . 6) . 7) . 8) .