7.5. Невласні інтеграли

Визначний інтеграл називають власним інтегралом, якщо проміжок інтегрування кінцевий, а підінтегральна функція f(x) безперервна на цьому відрізку. У даному розділі розглядаються так звані невласні інтеграли, тобто визначний інтеграл від безперервної функції, але з нескінченним проміжком інтеграції, або визначний інтеграл з кінцевим проміжком інтегрування, але від функції, що має в цьому інтервалі нескінченний розрив.

Невласний інтеграл I роду (інтеграл з нескінченним

проміжком інтегрування)

Хай підінтегральна функція f(x) безперервна і обмежена для всіх . Невласний інтеграл першого роду позначається як . Невласним інтегралом І роду від функції f(x) на нескінченному проміжку називається границя, якщо вона існує, при визначного інтеграла , тобто

= . (7.21)

Якщо ця границя існує і вона кінцева, то невласний інтеграл збігається. Якщо вказана границя не існує або вона нескінченна, то інтеграл називається розбіжним.

Аналогічним чином визначається невласний інтеграл на проміжку

= . (7.22)

Невласний інтеграл з двома нескінченними границями визначається формулою

= + , (7.23)

де с – довільне число. В даному випадку інтеграл зліва збігається у тому випадку, коли збігаються обоє інтеграла справа.

Приклади. Обчислити невласні інтеграли або встановити їх розбіжність:

1. = , інтеграл розбігається;

2. = = =

= ;

3. = , інтеграл розбіжний, оскільки при границя не існує.

4. Визначити площу фігури, обмеженою кривою і віссю Ох

= =

= .

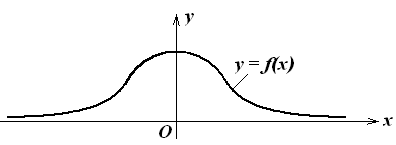
Рис. 7.19.

Ознаки порівняння

Приведемо без доведення одну з ознак збіжності невласних інтегралів I роду.

Теорема. Якщо на проміжку для безперервних функцій задовольняється нерівність 0 , то із збіжності інтеграла виходить збіжність інтеграла , з розбіжності інтеграла виходить розбіжність інтеграла .

Приклад. Досліджувати збіжність інтеграла . Підінтегральна функція на проміжку інтегрування менше ніж , а інтеграл сходиться. Отже, даний інтеграл також збігається.

Невласний інтеграл II роду (інтеграл від розривної функції)

Хай функція f(x) безперервна на проміжку і має нескінченний розрив в точці х = b . Невласним інтегралом II роду називається кінцева границя, якщо вона існує, інтеграла . Таким чином, за визначенням

. (7.18)

Якщо границя в правій частині існує, то невласний інтеграл збігається. Інакше невласний інтеграл розбігається.

Якщо функція f(x) має розрив в точці с на проміжку [а, b], то невласний інтеграл II роду визначається формулою

.

В цьому випадку інтеграл зліва збігається, якщо обоє невласних інтеграла справа збігаються.

Приклади. Обчислити або встановити збіжність невласного інтеграла:

1. . При х = 1 функція має нескінченний розрив.

=

2. . При х = 0 функція має нескінченний розрив.

= ,

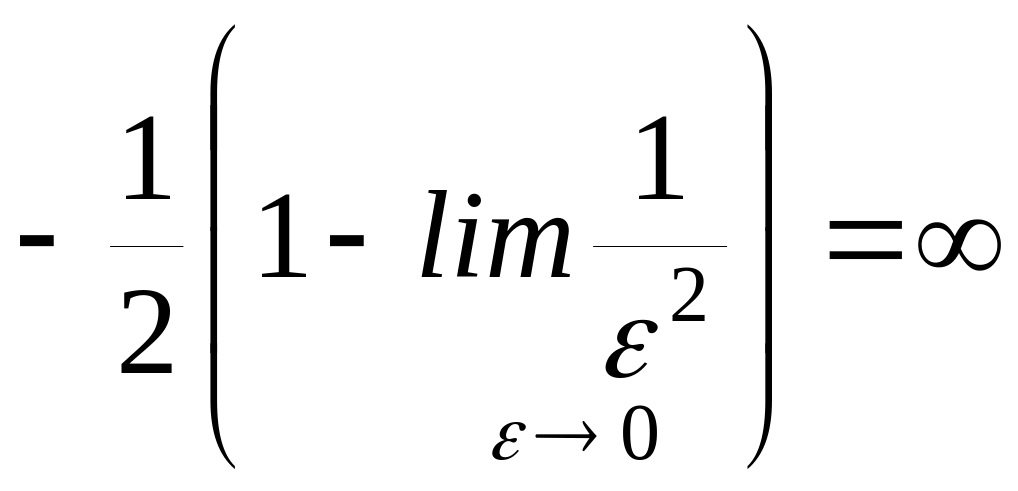інтеграл розбігається.

Приклади для самостійного розв‘язання

Обчислити невласні інтеграли:

1) . 2) . 3) . 4) .

5) . 6) .