
- •7. Визначний інтеграл
- •7.1.Поняття визначного інтеграла
- •7.2. Обчислення визначного інтеграла
- •7.3. Обчислення визначного інтеграла за допомогою пакету Maxima
- •Integrate(f, X, а, b)
- •7.4. Застосування визначного інтеграла
- •7.4.1. Обчислення площ плоских фігур
- •7.4.2. Визначення довжини дуги плоскої кривої
- •7.4.3. Обчислення об'єму тіла
- •7.4.4. Механічні застосування визначного інтеграла
- •7.5. Невласні інтеграли
- •7.6. Обчислення невласних інтегралів в середовищі Maxima
7. Визначний інтеграл
7.1.Поняття визначного інтеграла
Хай на відрізку [а, b] задана безперервна функція у = f(x). Розіб'ємо відрізок [а, b] на частини (не обов'язково однакові) n точками.
x0 < x1 < x2 < … < xn
Тоді x1 – x0 = x1, x2 – x1 = x2, … ,xn – xn-1 = xn – довжини часткових відрізків.
На
кожному з отриманих частковому відрізку
[xi-1,
xi],
i
= 1, 2,., n
виберемо довільну точку
![]() і знайдемо значення функції в цій точці,
тобто f(сi)
(див. рис. 7.1).
і знайдемо значення функції в цій точці,
тобто f(сi)
(див. рис. 7.1).
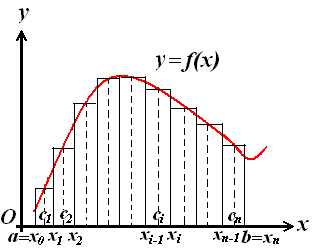
Рис. 7.1.
Складемо вираження Sn, яке називається інтегральною сумою для функції у = f(x) на відрізку [а, b].
Sn
= f(c1)x1
+ f(c2)x2
+ … + f(cn)xn
=
![]() .
.
Позначимо
λ
довжину найбільшого часткового відрізку:
![]() (i
= 1, 2,…, n).
Знайдемо границю інтегральної суми,
коли
(i
= 1, 2,…, n).
Знайдемо границю інтегральної суми,
коли
![]() так, що
так, що
![]() .
.
Якщо
при будь-якому розбиванні відрізка [а,
b]
на часткові таких, що maxxi
0
і довільному виборі точок сi
інтегральна сума
![]() прагне до границі I, то це число
називається визначним
інтегралом
від функції y
= f(x)
на відрізку [а,
b]
і позначається
прагне до границі I, то це число
називається визначним
інтегралом
від функції y
= f(x)
на відрізку [а,
b]
і позначається
![]()
Таким
чином
![]() =
=
![]() .
(7.1)
.
(7.1)
Числа
а
і b
називаються відповідно нижньою
і верхньою границями інтегралу,
х
– змінній інтегрування, [а,
b]
– відрізком інтегрування, f(x)
- підінтегральною функцією,
![]() - підінтегральним виразом.
- підінтегральним виразом.
Функція у = f(x), для якої на відрізку [а, b] існує визначний інтеграл називається інтегрованою на цьому відрізку.
З рисунку 7.1. видно, що сума добутків Sn = дорівнює площі ступінчастої фігури і приблизно дорівнює площі S криволінійної трапеції:
S ≈ Sn = .
Із зменшенням всіх величин xi криволінійної трапеції ступінчастою фігурою збільшується. Тому за точне значення площі криволінійної трапеції береться границя S, до якої прагне площа ступінчастої фігури Sn, коли n необмежено зростає так, що :
![]() =
,
тобто
S
=
.
=
,
тобто
S
=
.
Такий геометричний зміст визначного інтеграла.
Теорема (Коши). Якщо функція у = f(x) безперервна на відрізку [а, b], то вона інтегрована на цьому відрізку.
Існують і інші теореми математичного аналізу, що визначають класи функцій, інтегрованих на відрізку [а, b]. Зокрема такими є:
безперервні на відрізку [а, b] функції;
обмежені на відрізку [а, b] функції, що мають кінцеве число точок розриву;
монотонні на відрізку [а, b] функції.
Основні властивості визначного інтеграла
Розглянемо основні властивості визначного інтеграла, вважаючи підінтегральну функцію інтегрованою на відрізку [а, b]
 (С
– const), тобто постійний множник С можна
виносити за знак визначного інтеграла.
(С
– const), тобто постійний множник С можна
виносити за знак визначного інтеграла.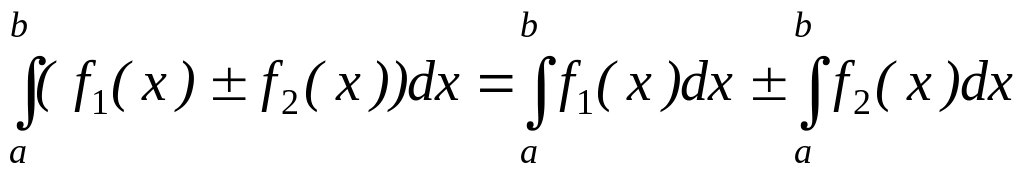 ,
тобто інтеграл від суми (різниці)
дорівнює сумі (різниці) інтегралів.
,
тобто інтеграл від суми (різниці)
дорівнює сумі (різниці) інтегралів.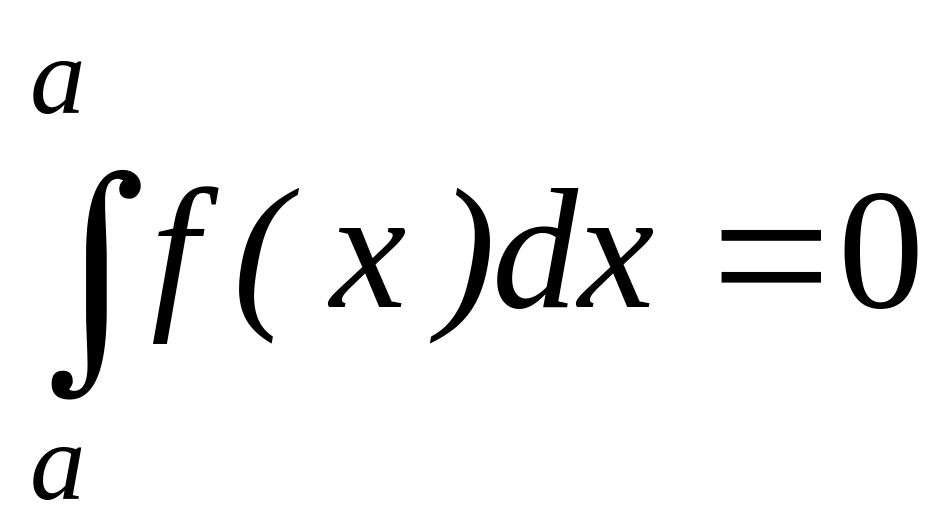 .
.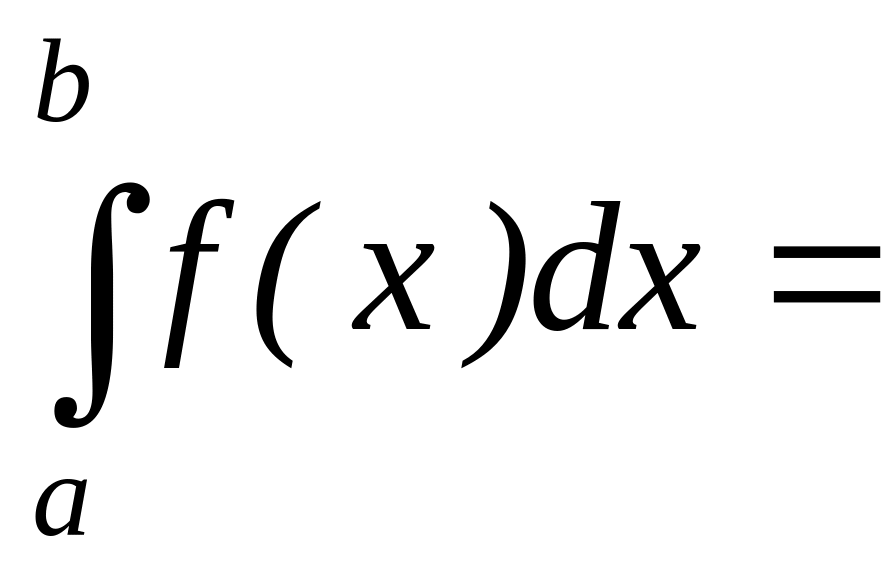
 .
.
5) Для довільних чисел а, b, с справедлива рівність:
![]() ,
тобто
інтеграл по всьому відрізку дорівює
,
тобто
інтеграл по всьому відрізку дорівює
сумі інтегралів по частинах цього відрізку.
Якщо функція f(x) зберігає знак на відрізку [а, b], де а < b, то інтеграл має той же знак, що і функція. Так якщо
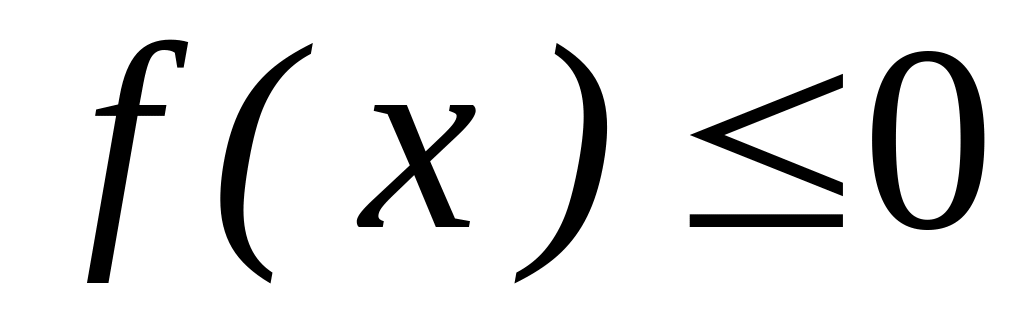 на відрізку [а, b], то
на відрізку [а, b], то

 .
.Якщо f(x) (x) на відрізку [а, b] (а < b), то
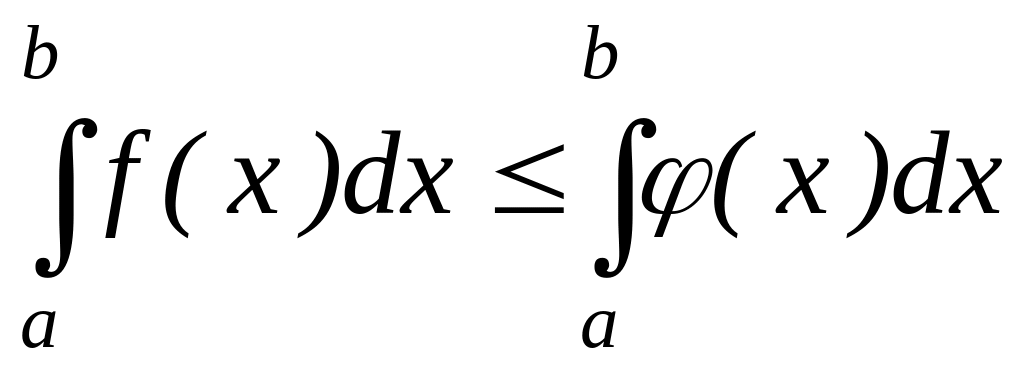 ,
тобто
нерівність між безперервними функціями
на відрізку
[а,
b]
(а
< b)
можна
інтегрувати.
,
тобто
нерівність між безперервними функціями
на відрізку
[а,
b]
(а
< b)
можна
інтегрувати.Якщо m і M – відповідно найменше і найбільше значення функції f(x) на відрізку [а, b] (а < b), то:
![]()
Теорема про середнє значення. Якщо функція f(x) безперервна на відрізку [а, b], то на цьому відрізку існує точка
 така, що
така, що
![]() .
.
Доведення: Відповідно до властивості 8:
або
![]() .
Позначимо
.
Позначимо
![]() .
.
Оскільки
функція f(x)
безперервна на відрізку [а,
b],
то вона набуває на цьому відрізку всіх
значень від m
до М.
Другими словами, існує таке число с
[a, b], що
= f(с),
тобто
![]() або
.
Теорема доведена.
або
.
Теорема доведена.
10) Похідна визначного інтеграла по змінній верхній границі дорівнює підінтегральної функції, в якій змінна інтегрування замінена цією границею
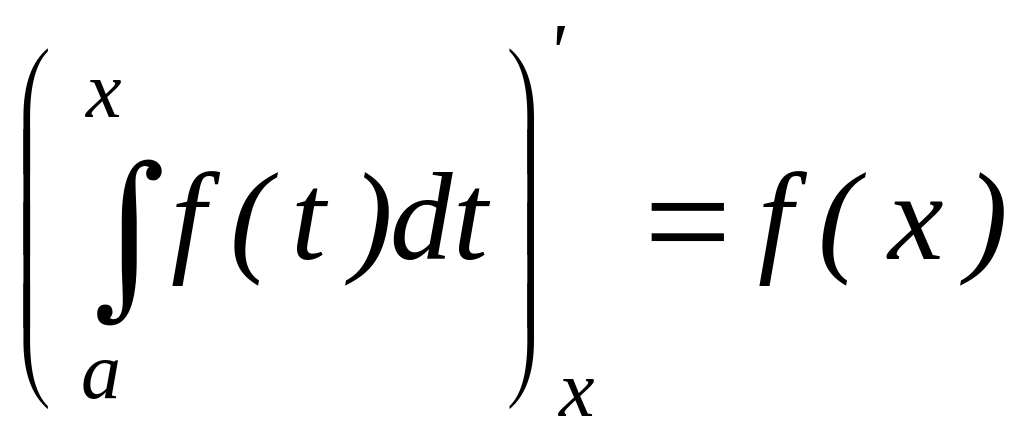
Доведення:
Хай
функція у
= f(x)
інтегрована на відрізку [а,
b].
Вводиться позначення
![]() ,
тут
,
тут
![]() . Розглянемо три точки відрізку [а,
b]:
а
, х та
х + Δх (
. Розглянемо три точки відрізку [а,
b]:
а
, х та
х + Δх (![]() )
і визначимо різницю
)
і визначимо різницю
![]() .
По властивості 5 визначних інтегралів
перший інтеграл правої частини можна
представити у вигляді суми
.
По властивості 5 визначних інтегралів
перший інтеграл правої частини можна
представити у вигляді суми
![]() . В результаті
. В результаті
![]() .
.
По
теоремі про середнє значення (властивість
9)
![]() ,
,
![]() .
.
Далі
обчислимо похідну функції
![]()
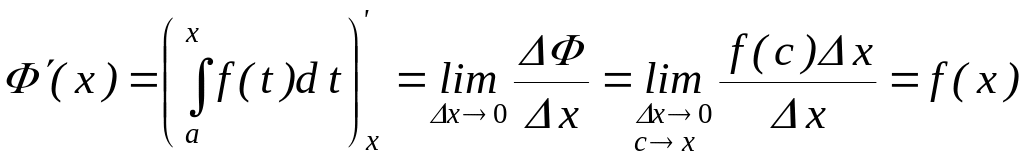 .
.
