Розкладання вектору по ортам координатних осей

Розглянемо прямокутну декартову систему координат (Оxyz) з початком відліку в точці О ( i, j, k - орты координатних осей). Нехай заданий вектор = ОА, початок якого співпадає з початком координат, тобто вектор = ОА є радіусом-вектором точки А.

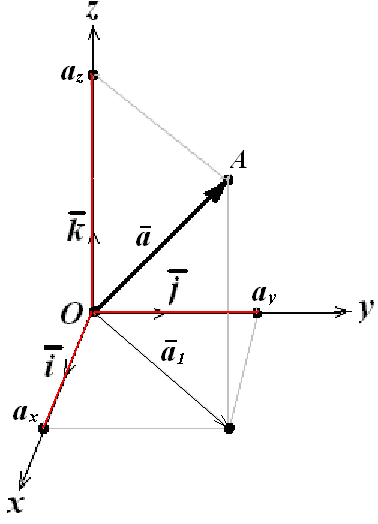
Рис. 3.7. Розкладання вектору по ортам осей координат.

Позначимо координати вектора на осі координат

a_x = Пр_x , a_y = Пр_y , a_z = Пр_z . (3.6)

Оскільки = + + (див. рис. 3.7) и = a_x i , = a_y j , = a_z k , те вектор має єдине розкладання по ортам осей координат

= a_x i + a_y j + a_z k . (3.7)

Скалярний добуток двох векторів

У фізичних і технічних додатках математики велике значення має рішення задачі про визначення роботи, яка здійснюється постійною силою F при переміщень матеріальної точки. Якщо точка переміщається прямолінійно, то, як відомо, робота дорівнює добутку величини сили на величину переміщення і на косинус кута між напрямом сили і напрямом переміщення. Позначивши силу F, а переміщення АВ, отримуємо для обчислення роботи вираз: A(F) = |F| ∙ |AB| ∙ cos(F^AB). Оскільки подібна "операція" з двома векторами зустрічається дуже часто, то для неї введено операція скалярного добутку.

Визначення 3.11. Скалярним добутком, двох векторів називається добуток їх довжин і косинуса кута між ними.

Скалярний твір двох векторів а і b означаємо символом a∙b. Відповідно до визначення

a ∙ b = | a | | b | cos(a ^ b). (3.8)

Властивості скалярного добутку

1. a ∙ b = b ∙ a ;

2. (α ∙ a) ∙ (β ∙ b) = α∙ β (a ∙ b) ;

3. (a + b) ∙ c = a ∙ c + b ∙ c ;

4. cos(a ^ b) = .

Звідки витікає, що умова ортогональності двох векторів(а _┴ b)

a ∙ b = 0. (3.9)

Обчислення скалярного добутку через координати векторів

Врахуємо, що орти прямокутної декартової системи координат мають наступну властивість:

i ∙ i =1 , j ∙ j =1, k ∙ k =1 , i ∙ j = 0, i ∙ k = 0, j ∙ k = 0.

Нехай задані вектори = a_x i + a_y j + a_z k і = b_x i + b_y j + b_z k . Визначимо скалярний добуток

a ∙ b = ∙ = (a_x i + a_y j + a_z k) ∙ (b_x i + b_y j + b_z k),

враховуючи властивості ортів координатних осей, отримаємо

∙ = a_x b_x + a_y b_y + a_z b_z . (3.10)

тобто скалярний добуток двох векторів дорівнює сумі добутків однойменних координат цих векторів.

Умова ортогональності двох векторів(а _┴ b)

a ∙ b = a_x b_x + a_y b_y + a_z b_z = 0. (3.11)

Векторний добуток двох векторів

Одним з найважливіших понять фізики, механіки і електродинаміки являються поняття моменту сили, моменту кількості руху, індукційний струм та ін. Наприклад, механічний ефект дії сили - прямо ліній поступальний рух, а механічний ефект від дії моменту сили - обертальний рух навколо деякої осі. Обчислення вказаних моментів пов'язано з векторним добутком двох векторів.

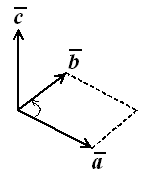
Визначення 3.12. Векторний добуток двох векторів і називається вектор , модуль якого дорівнює добутку модулів векторів - співмножників, перпендикулярний площині цих векторів і спрямований так, що з його кінця видно поворот від до по найкоротшому шляху, проти ходу годинникової стрілки.

= , (3.11)

1. | | = | | = | | | | sin( ^ ) ;

2. _┴ , _┴ ;

3.

Рис. 3.8. Векторний добуток [ ].

Зауваження. Модуль векторного добутку дорівнює площі паралелограма, побудованого на заданих векторах.

Властивості векторного добутку.

1). = - ;

2). (α ) (β ) = (α β) [ ] ;

3). ( + ) = + .

Обчислення векторного твору через координати векторів

Врахуємо, що орти прямокутної декартової системи координат мають наступну властивість:

i i =0 , i j = k , i k = - j ,

j i = - k , j j = 0 , j k = i ,

k i = j , k j = - i , k k = 0 .

Нехай задані вектори = a_x i + a_y j + a_z k і = b_x i + b_y j + b_z k . Визначимо скалярний твір

a b = = (a_x i + a_y j + a_z k) (b_x i + b_y j + b_z k),

враховуючи властивості ортів координатних осей, отримаємо

= (a_y b_z – a_z b_y) i + (a_z b_x – a_x b_z) j + (a_x b_y – a_y b_x) k . (3.12)

або = .

Важливим геометричним завданням, що вирішується за допомогою операції векторного добутку, є обчислення площі трикутника по координатах його вершин.

Нехай задані координати вершин трикутника A, B, C. Знаючи їх, знаходимо вектори АВ і АС. Площа трикутника АВС дорівнює половині площі паралелограма, побудованого векторах АВ і АС. Отже

S_ABC = ½ | АВ АС |. (3.13)

Приклад. A (1, -2,0), B(2,1,-1), C(0,3,1). Знайти S_ABC .

Розв‘язання. АВ = (1, 3, -1) , АС = (-1, 5, 1).

АВ АС = [3∙1 - (-1) ∙5] i + [(-1) ∙(-1) - 1∙1] j + [1∙5 - 3∙(-1)] k = 8 i + 8 k ,

| АВ АС | = 8 , S_ABC = 4 .

Мішаний добуток векторів.

Визначення 3.13. Скалярний добуток вектора на векторний добуток векторів і називається мішаним добутком векторів , і . Таким чином, мішаний добуток векторів, і є вираз

∙ ( ) (3.14)

і є скаляр (число).

З'ясуємо геометричний зміст введеного поняття. Нехай точка О є загальний початок трьох не компланарних векторів , , . Побудуємо на заданих векторах паралелепіпед (рис. 3.9) і знайдемо вектор = . З визначення скалярного добутку векторів, отримуємо ∙ ( ) = ∙ =

= | | Пр_d . Але оскільки вектор перпендикулярний площині векторів і , те проекція вектора на вісь, спрямовану по вектору , або дорівнює висоті паралелепіпеда. За визначенням довжина вектора дорівнює площі

паралелограма, побудованого на векторах і . Тому ∙ є об'єм паралелепіпеда.

Отже, абсолютна величина змішаного добутку трьох векторів дорівнює об'єму паралелепіпеда, побудованого на цих векторах.

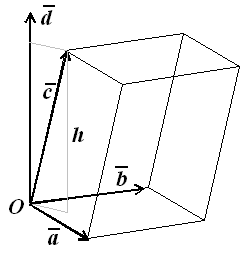
Рис. 3.9. Мішаний добуток векторів, , і .

Якщо в мішаному добутку трійки векторів їх переставляти, то паралелепіпед, побудований на вибраних векторах, очевидно, не зміниться. Значить, не зміниться і абсолютна величина мішаного добутку. Тому при круговій перестановці векторів мішаний добуток векторів не змінюється.

Отже

∙ ( ) = ∙ ( ) = ∙ ( ). (3.15)

Якщо вектори задані своїми координатами в деякій декартовій прямо-кутній системі координат (a_x , a_y , a_z) , (b_x , b_y , b_z), (c_x , c_y , c_z) , тому

вектор = = (b_yc_z - b_zc_y , b_zc_x - b_xc_z , b_xc_y - b_yc_x ). В результаті

∙ ( ) = a_x (b_yc_z - b_zc_y) + a_y (b_zc_x - b_xc_z) + a_z (b_xc_y - b_yc_x) (3.16)

або ∙ ( ) = .

якщо задані три вектори компланарні, то їх мішаний добуток дорівнює нулю.

Приклади для самостійного розв‘язання

Задані координати точок А(1,2,-3), B(-1,1,4), C (0,3,-5), D(2,-2,3). Знайти:

1) , 2) пр , 3) орт ,

4) , 5) площа , 6) пр ,

7) , 8) , 9) .

3.3. Прості завдання аналітичної геометрії

Як відомо з шкільної математики метод координат дає можливість встановити відповідність між деякими геометричними об'єктами і рівняннями. У школі розглядалася прямокутна система координат на площині (Оху) і говорилося про рівняння прямій, про рівняння параболи і графіку функції у = 1 / х і так далі. Зараз, використовуючи координатний метод і елементи векторної алгебри, ми вивчатимемо геометричні об'єкти із загальніших позицій. Раніше розглянемо прості завдання аналітичної геометрії.