3. Основи аналітичної геометрії

Аналітична геометрія вивчає прості геометричні об'єкти(прямі, площини, лінії і поверхні другого порядку) засобами алгебри на основі методу координат.

3.1. Метод координат

Положення точки А в просторі відносно деякої точки О (полюса) можна визначити за допомогою вектору ОА, кінець цього вектору вказує на розташування точки А в просторі відносно точки О.

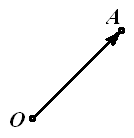
Рис. 3.1. Радіус - вектор точки А

Через точку О в просторі проведемо три взаємно перпендикулярні осі, і на кожній з них візьмемо одиничний вектор, спрямований по цій осі (орт осі). Вісь з початком відліку в точці О і одиницею довжини називається координатної віссю, а впорядкована система трьох взаємно перпендикулярних координатних осей із загальним початком відліку О і загальною одиницею довжини, називається прямокутною декартовою системою координат в просторі. У вибраній впорядкованій системі координатних осей першу вісь будемо називати віссю абсцис (чи віссю х), другу - віссю ординат (чи віссю у), третю - віссю аплікат (чи віссю z).

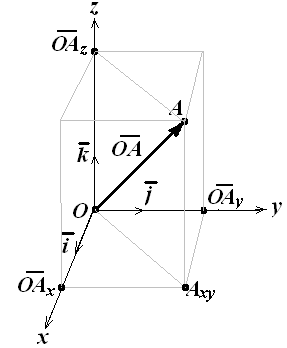
Рис. 3.2. Координатний метод завдання положення точки А в просторі.

Визначення 3.1. Координатами точки в заданій прямокутній Декартові системі координат називаються проекції радіусу-вектору цієї точки на координатні осі.

Координати точки А в заданій прямокутній декартовій системі координат (рис. 3.2) записуються у виді (x, y, z), де

x = OA_x = Пр_х ОА , y = OA_y = Пр_y ОА , z = OA_z = Пр_z ОА, (3.1)

і називаються відповідно абсцисою, ординатою і аплікатою точки А.

Довжина вектора ОА визначається діагоналлю паралелограма із сторонами x, y, z, тобто

. (3.2)

3.2. Елементи векторної алгебри.

Геометричною моделлю векторної величини є прямолінійний відрізок з вибраним на нім напрямом.

Визначення 3.2. Вектор AB - спрямований відрізок прямої, у якого один кінець (точка А) називається початком вектору, а інший кінець (точка В) - кінцем вектора.

До векторів відноситься також і нульовий вектор, початок і кінець якого збігаються.

Використовуючи координатний метод всякий вектор в заданій впорядкованій декартовій системі координат представляється алгебраїчним об'єктом у вигляді впорядкованої трійки чисел (x, y, z), де x, y, z - координати радіус-вектора AB (точка А - початок координат), або координати кінця В вектора AB.

Визначення 3.3. Довжина (модулем) вектора називається відстань між початком і кінцем вектора.

,

де координати точок А(0,0,0) - початок координат, В(x, y, z) (див. рис. 3.2)

Визначення 3.4. Вектори називаються колінеарними, якщо вони розташовані на одній прямій або на паралельних прямих. Нульовий вектор колінеарен будь-якому вектору.

Визначення 3.5. Вектори називаються компланарними, якщо існує площина, якій вони паралельні.

Визначення 3.6. Вектори називаються рівними, якщо вони колінеарні, однаково спрямовані і мають однакові модулі.