1.4. Основи роботи в середовищі комп'ютерної алгебри Maxima і перетворення алгебраїчних виразів.

Введення простих команд в wxMaxima

Після запуску wxMaxima з'являється вікно програми, яке показане на рис. 1.

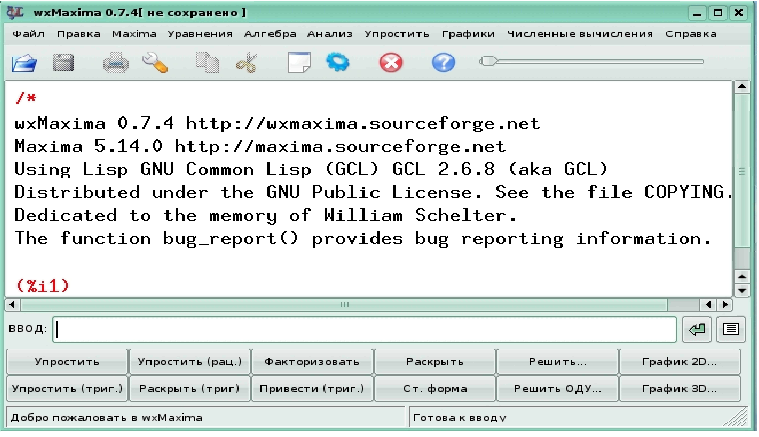
Рис 1. Графічний интерфейс wxMaxima

У верхній графічній частині вікна інтерфейсу Maxima інформується, що завантажена версія 5.14.0, що вона поширюється за ліцензією GNU, з якого сайту доступна. У нижньому вікні в полі ВВЕДЕННЯ: Maxima приготувалася

сприймати команди. Роздільником команд є символ ; (крапка з комою). Після введення команди необхідно натиснути клавішу Enter для її обробки і виве-дення результату.

Позначення команд і результатів обчислень

Після введення кожній команді привласнюється порядковий номер. На приведеному нижче малюнку введені команди мають номери 1-3 і позначаються відповідно (%i1), (%i2), (%i3). Результати обчислень мають відповідно порядковий номер (%o1), (%o2) і т. д. Де "i" -сокращение від англ. input(введення), а "o" - англ. output(виведення).

Цей механізм дозволяє при подальшому записі команд послатися на раніше записані, наприклад (%i1)+(%i2) означатиме додавання до виразу першої команди вираз другої з подальшим обчисленням результату. Також можна використати і номери результатів обчислень, наприклад, таким чином (%o1)*(%o2). Для останньої виконаної команди в Maxima є спеціальне позначення - %.

Приклад: Обчислити значення похідної функції

в точці х = 1

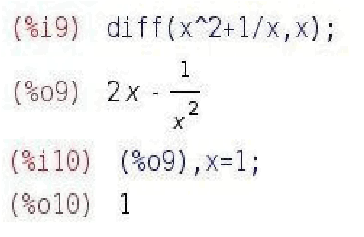
Введення числової інформації

Правила введення чисел в Maxima такі самі, як і для багатьох інших подібних програм. Ціла і дробова частина десяткових дробів розділяються символом точка. Перед негативними числами ставиться знак мінус. Чисель-ник і знаменник звичайних дробів розділяється за допомогою символу / (прямий слеш).

Зверніть увагу, що якщо в результаті виконання операції виходить деякий символьний вираз, а необхідно отримати конкретне числове значення у вигляді десяткового дробу, то вирішити це завдання дозволить застосу-вання оператора numer. Зокрема він дозволяє перейти від звичайних дробів до десяткових.

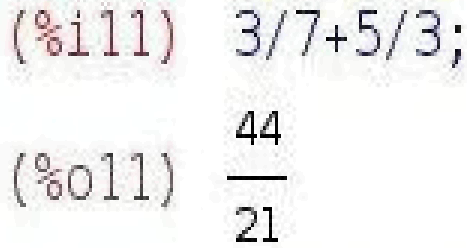
Константи

У Maxima для зручності обчислень є ряд вбудованих констант, найпоширеніші з них показані в наступній таблиці (таблиця 1) :

Таблиця 1. Основні константи Maxima

Назва	Позначення
плюс нескінченність	inf
мінус нескінченність	minf
число π	%pi
e (експонента)	%e
Уявна одениця √−1	%i

Арифметичні операції

Позначення арифметичних операцій в Maxima нічим не відрізняються від класичного представлення, використовуються математичні знаки: + - * /.

Піднесення до степеня можна означати трьома способами: ^, ^^, **. Витягання кореня степені n записують, як степінь ^^ (1/n).

Нагадаємо ще одну вбудовану в Maxima корисну операцію - знаходження факторіалу числа. Ця операція позначається знаком оклику.

Наприклад, 6!=1× 2× 3× 4× 5× 6=120.

Для збільшення пріоритету операції, як і в математиці, при записі команд для Maxima використовують круглі () дужки.

Змінні

Для зберігання результатів проміжних розрахунків застосовуються змінні. Помітимо, що при введенні назв змінних, функцій і констант важли-вий регістр букв, так змінні x і X - це дві різні змінні.

Надання значення змінній здійснюється з використанням символу: (дво-крапка), наприклад x: 5;. Якщо необхідно видалити значення змінної (очистити її), то застосовується метод kill :

kill(x) - видалити значення змінної x;

kill(all) - видалити значення усіх використовуваних раніше змінних.

Математичні функції

У Maxima є досить великий набір вбудованих математичних функцій. Ось деякі з них (таблиця 2). Слід мати на уваженні, що деякі назви функцій відрізняються від назв, які використуються у вітчизняній літературі : замість tg - tan, замість ctg - cot, замість arcsin - asin, замість arccos - acos, замість arctg - atan, замість arcctg - acot, замість ln - log, замість cosec - csc.

Таблиця 2. Вбудовані математичні функції

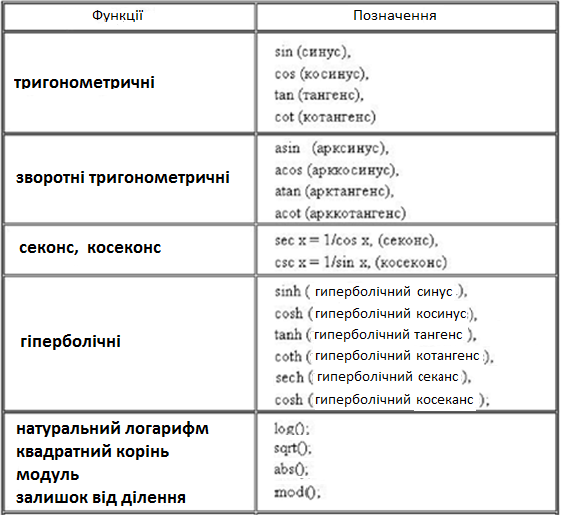
Правило запису функцій

Для запису функції необхідно вказати її назву, а потім, в круглих дужках записати через кому значення аргументів. Якщо значенням аргументу є список, то він полягає в квадратних дужках, а елементи списку також розділяються комами.

Приклад:

sin(x);

integrate(sin(x), x, - 5,5); plot2d([sin(x)+3, cos(x)],[x,-%pi, %pi],[y,-5,5]);

Функції користувача

Користувач може задати власні функції. Для цього спочатку вказується назва функції, в дужках перераховуються назви аргументів, після знаків := (двокрапка і рівна) слідує опис функції. Після завдання функція, яка призначена для користувача, викликається точно так, як і вбудовані функції Maxima.

Приклад:

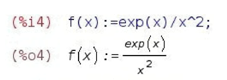
Розв‘язок задач елементарної математики

До таких задач можна віднести обчислення і перетворення арифметичних виразів, побудову графіків функцій, розв‘язання рівнянь і систем алге-браїчних рівнянь.

Maxima спрощує вирази

Розглянемо можливості Maxima по спрощенню і іншим перетворенням виразів. Зокрема, мова піде про автоматичне розкриття дужок і винесення за дужки; про спрощення як арифметичних дій над деякими елементами, так і виразів за участю степеневих, показникових і логарифмічних функцій; а також про обробку тригонометричних виразів. Усі ці функції покликані полегшувати читаність математичних формул і підвищувати простоту їх сприйняття, а тому варто приділити цьому досить уваги: при вірному використанні ці маніпуляції дозволять заощадити в процесі роботи значну кількість часу.

Істотна частина тих, що цікавлять нас передусім функцій призначена для перетворення раціональних виразів. Математики називають раціональними такі вирази, що складаються тільки з арифметичних операторів і піднесення до натурального степеня.

Імена усіх функцій Maxima по обробці раціональних виразів містять букво друкувальне rat, від слова rational. І почнемо ми з функцією, яка так і називається : rat(вираження). Ця функція перетворює раціональний вираз до так званої канонічної форми. Тобто розкриває усі дужки, потім приводить все до спільного знаменника, підсумовує і скорочує; крім того, приводить усі числа в кінцевому десятковому записі до раціональних.

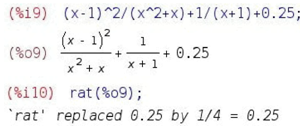
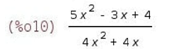
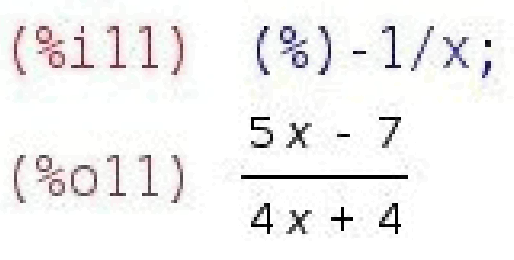
Це може бути досить зручно, якщо вам треба покроково виконати велику кількість раціональних перетворень : ви можете, один раз викликавши rat(); посилатися на попередні осередки і, завдяки цьому, далі автоматично бачити на кожному кроці підсумкове вираження в канонічній, тобто досить компактній і зручній до сприйняття формі.

Тут, хоча і був вираз в канонічній формі, вираз (%26) вже не знаходиться в канонічній формі з огляду на те, що були перетворення log(exp()). Вираз (%27) отримав канонічну форму в результаті дії функції rat(); а вираз (%28) після застосування функції ratdisrep( ) має загальний вигляд.

У багатьох випадках для отримання найбільш простого результату вимагається записати вираз у вигляді суми простих дробів. Таку задачу вирішує функція partfrac(), їй тільки треба вказати ім'я змінної, відносно якої вона зробить такі перетворення.

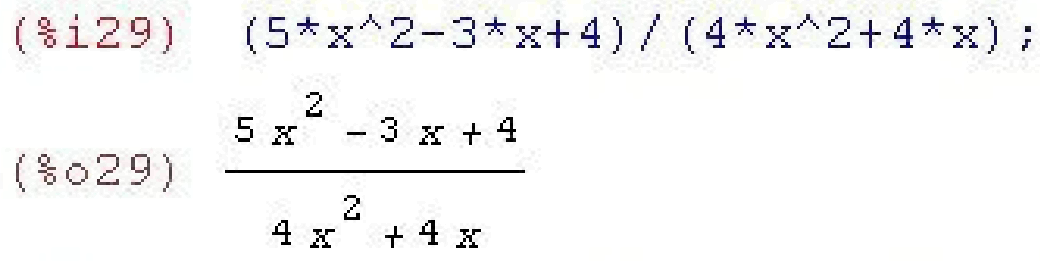
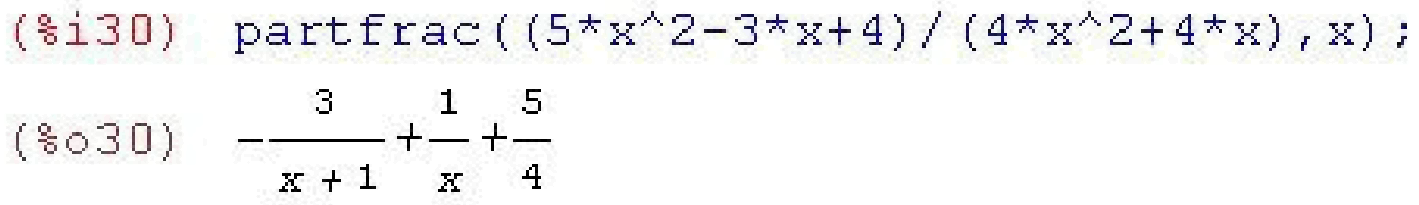
Розкриття дужок

Наступна функція розкриває дужки в раціональному виразі і називається ratexpand(); (одно зі значень слова expand і є "розкриття дужки"). Тут також діє опція keepfloat. Окрім неї, є ще одна опція - ratdenomdivide; за умовчанням вона встановлена в true, це призводить до того, що кожен дріб, в якому чисельник є сумою, розпадається на суму дробів з однаковим знамен-ником. Якщо ж скинути цю опцію в false, тоді усі дроби з однаковим знаменником будуть, навпаки, об'єднані в один дріб з чисельником у вигляді суми чисельників первинних. Тобто зовні результат в цьому випадку виглядатиме майже так само, як і у функції rat(); до того ж єдина видима користувачеві різниця проявляється тільки в раціональних виразах від декількох змінних(чи різних ірраціональних виразів). Полягає ця різниця в тому, що після ratexpand(); і у чисельнику, і в знаменнику дробу усі дужки будуть розкриті, у разі ж rat(); доданки, де є присутніми, скажімо, дві змінних, будуть згруповані, і одна з них буде винесена за дужки:

Крім того, різниця, звичайно, полягає і у внутрішньому уявленні: з точки зору програми, після ratexpand(); вираз буде як і раніше загального вигляду. Відповідно і усі результати подальших раціональних дій з виразами автоматично не "канонізуватимуться".

Наступна функція, збирає воєдино дроби з однаковими знаменниками; звуть її - combine()

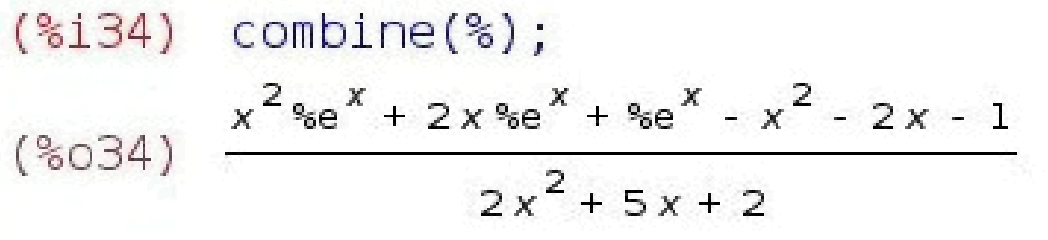
Відмітимо, що інтерфейс wxMaxima дозволяє набирати ім'я функцій ratsimp(); radcan(); factor(); expand(); у "одно торкання" клацанням миші (Рис.2). Якщо після запису в полі ВВЕДЕННЯ якого-небудь вираз клацнути мишею по відповідній кнопці Спростити, Спростити(рац), Факторизовать, Розкрити, те введений вираз розглядатиметься як аргумент функції, математичні назви яких показані у вигляді другого рядка на мал. 2, "сховані" під кнопками. Якщо поле ВВЕДЕННЯ було не заповнено, то як аргумент функції використовуватиметься результат останньої виконаної команди (%).

Аналогічно під кнопками Спростити(триг), Розкрити(триг), Привести(триг) "ховаються" функції trigsimp(); trigexpand(); trigreduce();, які працюють з тригонометричними виразами.

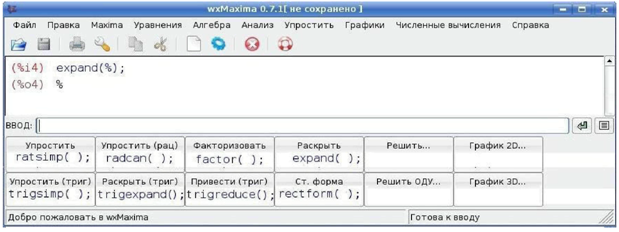
Рис. 2. Функції і кнопки інтерфейсу wxMaxima, що їм відповідають

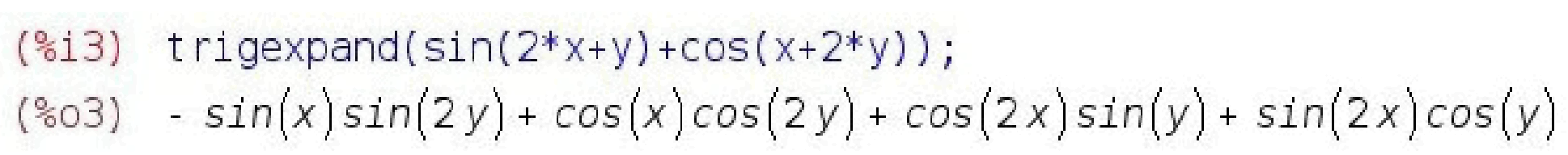
Функція, зворотна trigexpand(); називається trigreduce();

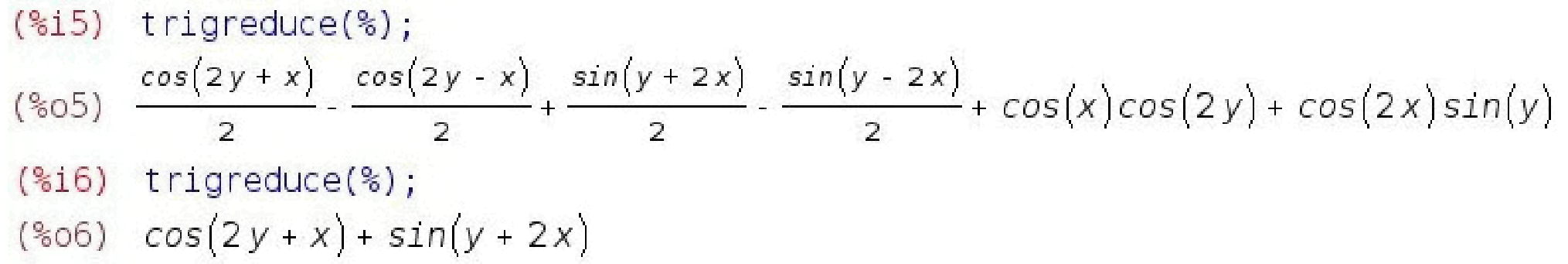
- тут, в повній відповідності зі значенням слова reduce, діються формули пониження степені.

Розв‘язок рівнянь

Рівняння і системи рівнянь вирішуються в Maxima одній і тій же функциией solve. Інтерфейс wxMaxima дозволяє спростити процедуру використання функції solve : після натиснення на кнопку Вирішити... з'явиться додаткове вікно Вирішити, в якому конкретизується і вид рівняння, і ім'я змінної, відносно якої треба вирішити рівняння (рис. 3).

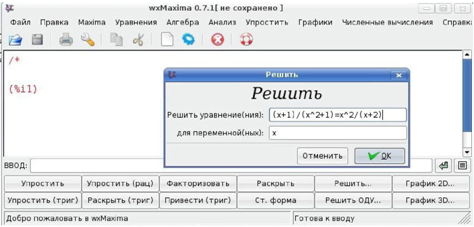
Рис.3. Інтерфейс wxMaxima для розв‘язку рівняння

Втім, інтерфейс wxMaxima можна не використати, можна просто написати команду для Максими виду solve([(x+1)/(x^2+1)=x^2/(x+2)], [x]);

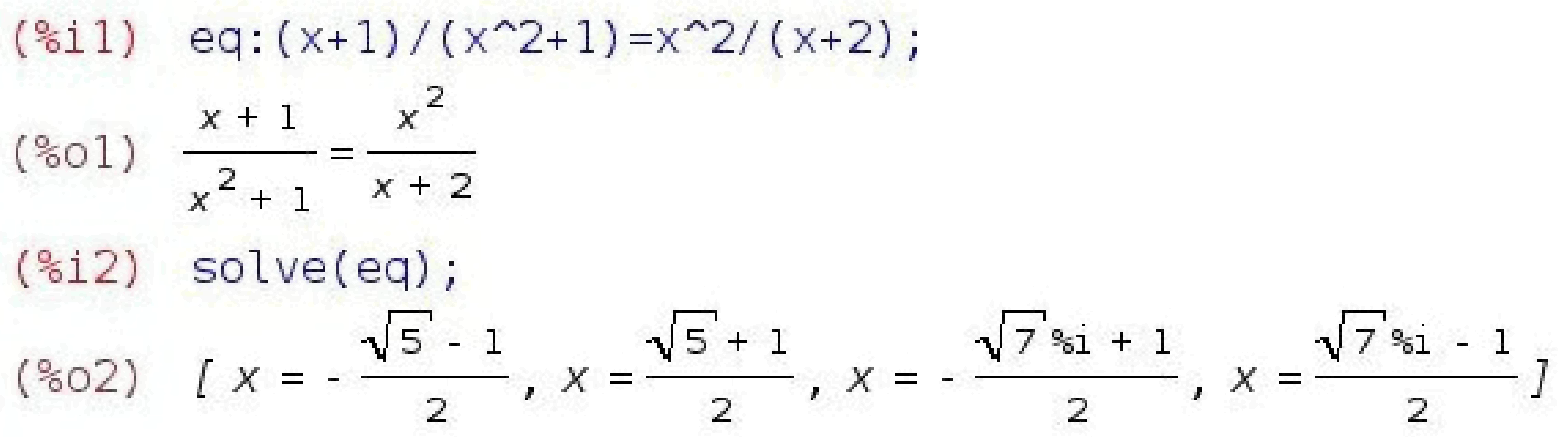
Тут ми спочатку записали рівняння (команда %i1). Потім попросили вирішити його за допомогою функції solve(команда %i2).