6.5.2. Визначення довжини дуги плоскої кривої

Прямокутні координати

Під довжиною дуги АВ розуміється границя, до якої прагне довжина ламаної лінії, вписаної в цю дугу, коли число сторін ламаної необмежено зростає, а довжина найбільшої із сторін ламаної прагне до нуля (Рис. 6.14).

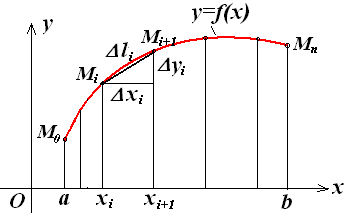
Рис. 6.14.

. (6.9)

Приклад. Обчислити довжину дуги кубічної параболи , що знаходиться між точками і .

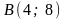Оскільки 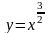, то 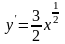. Тому шукана довжина дуги згідно формулі (6.9) визначається таким чином

= .

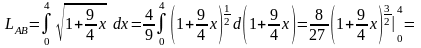
Параметричні координати. Якщо рівняння кривої задане пара-метрично, те довжина дуги кривої

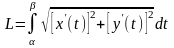. (6.10)

Приклад. Знайти довжину першої арки циклоїди

Знаходимо похідні і 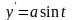. По формулі (6.10) довжина арки циклоїди

=

=

= .

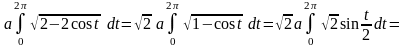
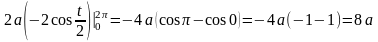Полярні координати. Хай крива задана в полярних координатах, , . Довжина кривої визначається формулою

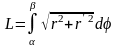. (6.11)

Приклад. Знайти довжину кардіоїди . Кардіоїда (Рис. 6.15)

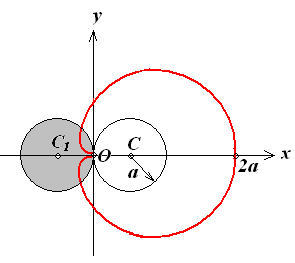
Рис. 6.15

може бути отримана як траєкторія точки кола С₁, що котиться без ковзання по колу С того ж радіусу а. Коли φ пробігає проміжок (-π, +π) , кардіоїда описується повністю. Довжина її згідно (6.11) дорівнює

.

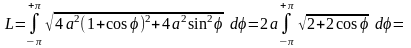
6.5.3. Обчислення об'єму тіла

Якщо відомі площі його поперечних перетинів

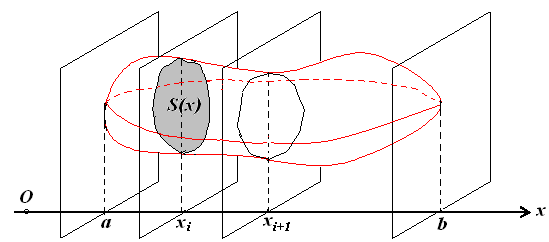
Рис. 6.16.

. (6.12)

Об'єм тіла обертання

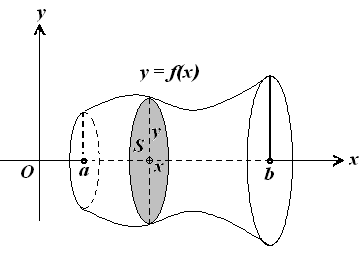
Рис. 6.17.

. (6.13)

Приклад. Визначити об'єм тіла, утвореного обертанням фігури, обмеженої лініями y = x² , x = 1, x = 2 (рис. 6.18).

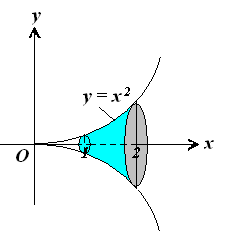
Рис. 6.18.

Розв‘язання. За формулою (7.14) знаходимо

= .

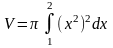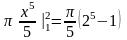Приклади для самостійного розв‘язку

Обчислити площу фігури, яка обмежена лініями

6.65. 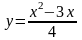, х = 5. Відповідь:

6.66. 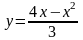, у = 0. Відповідь:

6.67. , y = 10 x. Відповідь:

6.68. 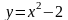, y = 4. Відповідь:

6.69. , y = x + 1. Відповідь:

6.70. 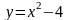, 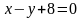. Відповідь:

6.71. 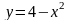, . Відповідь:

6.72. 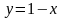, 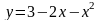. Відповідь:

6.73. Відповідь:

6.74. Відповідь:

6.75. 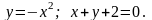Відповідь:

6.76. 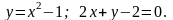Відповідь:

6.77. Відповідь:

6.78. Відповідь:

6.79. 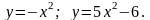  Відповідь:

6.80. , , Відповідь:

Обчислити довжину кривої, яка задана рівняннями

6.81. 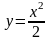між точками А(1;1) та В(2;4). Відповідь:

6.82. , що відтинається прямою у = х. Відповідь:

6.83. від точки х = 0 до точки х = 1. Відповідь:

6.84. 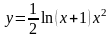від точки х = 0 до точки х = 1. Відповідь:

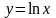
6.85. . Відповідь:

6.86. . Відповідь:

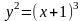
6.87. 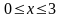. Відповідь:

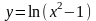
6.88. 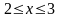. Відповідь:

6.89. Відповідь:

6.90. 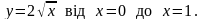Відповідь:

6.91. Відповідь:

6.92. Відповідь:

6.93. Відповідь:

6.94. 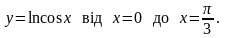Відповідь:

Обчислити об‘єм тіла, утвореного обертанням фігур: обмеженої лініями

6.95. та віссю абсцис навколо вісі Оx. Відповідь:

6.96. та прямою х = 2 навколо осі абсцис. Відповідь:

6.97. 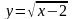та прямою у = 2, навколо осі абсцис. Відповідь:

6.98. навколо осі абсцис. Відповідь:

6.99. 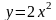та прямою х = 1 навколо осі абсцис. Відповідь:

6.100. . Відповідь:

6.102. . Відповідь:

6.103. . Відповідь:

6.104. . Відповідь:

6.105. 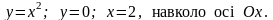Відповідь:

6.106. 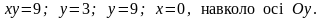Відповідь:

6.107. 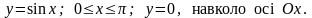Відповідь:

6.108. 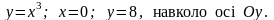Відповідь:

6.109. Відповідь:

6.110. 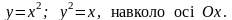Відповідь: