
- •6. Визначний інтеграл
- •6.1. Основні визначення і формули.
- •Якщо функція f(X) неперервна на відрізку [а, b], то на цьому відрізку існує
- •6.2. Обчислення визначного інтеграла
- •6.4. Обчислення визначного інтеграла за допомогою пакету Maxima
- •6.5. Застосування визначного інтеграла
- •6.5.1. Обчислення площ плоских фігур
- •6.5.2. Визначення довжини дуги плоскої кривої
- •6.5.3. Обчислення об'єму тіла
- •Приклади для самостійного розв‘язку
- •6.6. Невласні інтеграли
- •6.117. Відповідь: 6.118. Відповідь:
- •6.119. Відповідь: 6.120. Відповідь:
- •6.121. Відповідь: 6.122. Відповідь:
- •6.7. Обчислення невласних інтегралів в середовищі Maxima
6. Визначний інтеграл
6.1. Основні визначення і формули.
Якщо
при будь-якому розбиванні відрізка [а,
b]
на часткові таких, що maxxi
0
і довільному виборі точок сi
ϵ xi
інтегральна сума
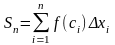 прагне до границі I, то це число
називається визначним
інтегралом
від функції y
= f(x)
на відрізку [а,
b]
і позначається
прагне до границі I, то це число
називається визначним
інтегралом
від функції y
= f(x)
на відрізку [а,
b]
і позначається

Таким
чином
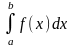 =
=
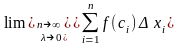 .
(6.1)
.
(6.1)
Основні властивості визначного інтеграла
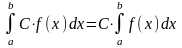 (С
– const),
(С
– const),
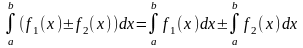 .
.
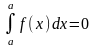 .
.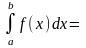
 .
.
5) Для довільних чисел а, b, с справедлива рівність:
 .
.
Якщо функція f(x) зберігає знак на відрізку [а, b], де а < b, то інтеграл має той же знак, що і функція.], то
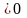 (якщо
(якщо
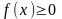 ),
або
(якщо
),
або
(якщо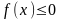 ).
).
Якщо f(x) (x) на відрізку [а, b] (а < b), то
 .
.Якщо m і M – відповідно найменше і найбільше значення функції f(x) на відрізку [а, b] (а < b), то:
 .
.
Якщо функція f(X) неперервна на відрізку [а, b], то на цьому відрізку існує
точка
 така, що
така, що
 .
.
10) Похідна
визначного інтеграла по змінній верхній
границі дорівнює підінтегральної
функції
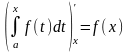 .
.
6.2. Обчислення визначного інтеграла
Формула
Ньютона-Лейбніца.
 .
(6.2)
.
(6.2)
Формула Ньютона – Лейбніца є загальний підхід до знаходження визначних інтегралів, якщо відома первісна функція F(x).
Приклади. Обчислити інтеграл
1.
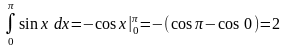 ;
;
2.
 ;
;
3.
 .
.
Інтегрування підстановкою (заміна змінної x = (t))
 .
(6.3)
.
(6.3)
Приклад.
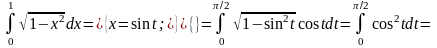

Інтегрування
частинами
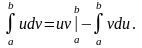 (6.4)
(6.4)
6.3. Задачі для самостійного розв‘язку
Обчислити визначний інтеграл
a). За допомогою формули Ньютона-Лейбниця, знайти інтеграли
6.1.
 .
Відповідь: 6.2.
.
Відповідь: 6.2.
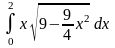 .
Відповідь:
.
Відповідь:
6.3.
 .
Відповідь: 6.4.
.
Відповідь: 6.4.
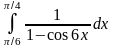 .
Відповідь:
.
Відповідь:
6.5.
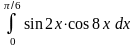 .
Відповідь: 6.6.
.
Відповідь:
.
Відповідь: 6.6.
.
Відповідь:
6.7.
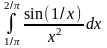 .
Відповідь:
.
Відповідь:
b). Обчислити інтеграли за допомогою метода підстановки
6.8.
 . Відповідь: 6.9.
. Відповідь: 6.9.
 . Відповідь:
. Відповідь:
6.10.
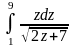 . Відповідь: 6.11.
. Відповідь: 6.11.
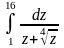 . Відповідь:
. Відповідь:
6.12.
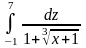 .
Відповідь: 6.13.
.
Відповідь: 6.13.
 .
Відповідь:
.
Відповідь:
6.14. 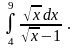 Відповідь:
6.15.
Відповідь:
6.15.  Відповідь:
Відповідь:
6.16.  Відповідь: 6.17.
Відповідь: 6.17.
 Відповідь:
Відповідь:
6.18.  Відповідь:
6.19.
Відповідь:
6.19. 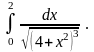 Відповідь:
Відповідь:
6.20.
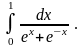 Відповідь:
6.21.
Відповідь:
6.21.
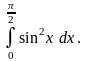 Відповідь:
Відповідь:
6.22. 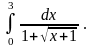 Відповідь: 6.23.
Відповідь: 6.23.  Відповідь:
Відповідь:
c). Обчислити інтеграли за допомогою метода інтегрування частинами
6.24.
 . Відповідь: 6.25.
. Відповідь: 6.25.
 .
Відповідь:
.
Відповідь:
6.26.
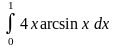 .
Відповідь: 6.27.
.
Відповідь: 6.27.
 .
Відповідь:
.
Відповідь:
6.28.
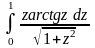 Відповідь: 6.29.
Відповідь: 6.29.
 .
Відповідь:
.
Відповідь:
6.30.
 .
Відповідь: 6.31.
.
Відповідь: 6.31.
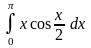 .
Відповідь:
.
Відповідь:
6.32. 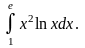 Відповідь:
6.33.
Відповідь:
6.33.
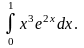 Відповідь:
Відповідь:
6.34.
 Відповідь:
6.35.
Відповідь:
6.35.
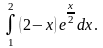 Відповідь:
Відповідь:
6.36.
 Відповідь:
6.37.
Відповідь:
6.37.
 Відповідь:
Відповідь:
6.38.
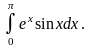 Відповідь:
6.39.
Відповідь:
6.39.
 Відповідь:
Відповідь:
d) Застосовуючи різні методи інтегрування, обчислити такі визначені
інтеграли:
6.40.
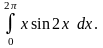 Відповідь:
6.41.
Відповідь:
6.41.
 Відповідь:
Відповідь:
6.42.
 Відповідь:
6.43.
Відповідь:
6.43.
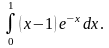 Відповідь:
Відповідь:
6.44.
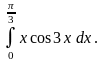 Відповідь:
6.45.
Відповідь:
6.45.
 Відповідь:
Відповідь:
6.46.
 Відповідь:
6.47.
Відповідь:
6.47.
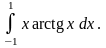 Відповідь:
Відповідь:
6.48.
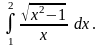 Відповідь:
6.49.
Відповідь:
6.49.
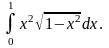 Відповідь:
Відповідь:
