8.2.1.1.4 Течение вязкопластичной среды Шведова-Бингама в круглой трубе

Необходимо получить распределение напряжения сдвига и скорости по радиусу круглой трубы при течении в ней жидкости Шведова-Бингама.

Составив элементарный баланс сил для потока жидкости Шведова-Бингама в круглой трубе, можно получить функцию

(8.17а)

совпадающую с соотношением (8.17), полученным в п. 8.1.3.4 для случая течения ньютоновской жидкости в круглой трубе с внутренним радиусом .

Распределение касательного напряжения по радиусу круглой трубы представлено на рис. 8.7, б.

Из соотношения (8.17а) видно, что минимальное напряжение сдвига действует на оси трубы при , а максимальное по абсолютной величине напряжение сдвига имеет место на внутренней поверхности трубы при

В соотношении (8.17а) использованы обозначения:

– проекция градиента давления на ось z;

– перепад давления между сечениями трубы с координатами и , расстояние между которыми равно

В приосевой области действует напряжение сдвига меньшее, чем предел текучести Поэтому в этой области среда Шведова-Бингама будет двигаться как твердый цилиндрический стержень с наружным радиусом . Величину этого радиуса с учетом соотношения (8.17а) можно вычислить исходя из условия, что , т.е.

откуда следует

или

Из закона течения (8.24) жидкости Шведова-Бингама, запись которого

справедлива при , следует, что ранее полученное соотношение (8.23) можно представить в виде

(8.23а)

Рассмотрим (8.23а) подробнее. В пределах

Вычислив неопределенный интеграл, получаем что

т.е. в пределах скорость течения жидкости Шведова-Бингама остается постоянной. Величина этой постоянной скорости течения, часто обозначаемая , будет найдена ниже.

Рассмотрим (8.23а) при

С учетом того что после интегрирования в пределах от до

получаем

;

,

где принято во внимание, что

Подставив в последнюю формулу, получим величину скорости в пределах участка

.

С учетом того что получим

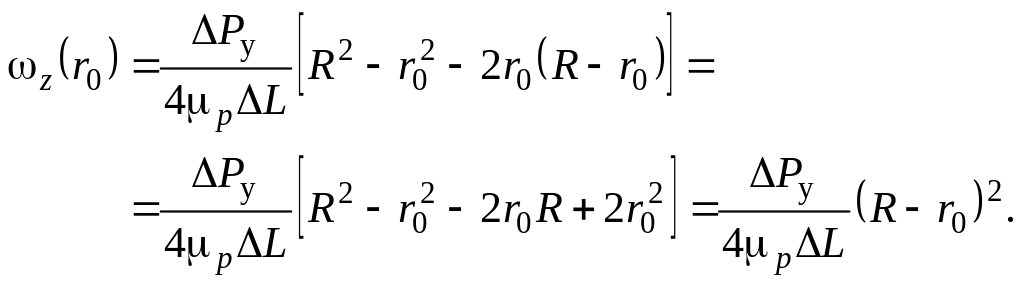
С учетом последнего соотношения зависимость скорости течения жидкости Шведова-Бингама от радиуса (при течении в круглой трубе) можно записать в виде

(8.26)

После интегрирования (8.26) получим формулу для вычисления расхода жидкости Шведова-Бингама через трубу с внутренним радиусом

. (8.26а)

Приняв во внимание, что абсолютная величина предела текучести равна соотношение (8.26а) можно представить в виде формулы

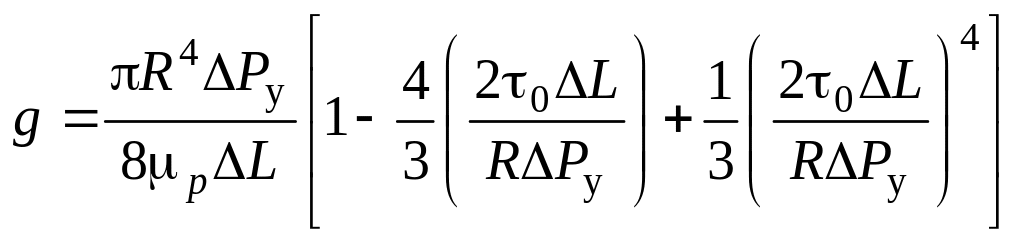, (8.26b)

известной как формула Букингема-Рейнера [33].

Формулу (8.26b) не удается разрешить относительно перепада давления При формула Букингема-Рейнера (8.26b) переходит в известную формулу Пуазейля (8.14).

Средняя скорость течения жидкости Шведова-Бингама в круглой трубе вычисляется следующим образом

. (8.26с)

Отметим, что при формула (8.26с) переходит в формулу (8.13а), полученную ранее для ламинарного «пуазейлевского» течения ньютоновских жидкостей.

Долгое время модель (8.24а) рассматривалась как почти универсальная для всех вязкопластичных систем, в первую очередь таких, где дисперсная фаза образует каркасные структуры коагуляционного типа. С развитием методов и аппаратуры реометрии обнаружилась нелинейность кривой течения , в ряде случаев распространяющаяся на несколько десятичных порядков изменения скорости сдвига .