8.1.4.2 Распределение касательного напряжения по радиусу при установившемся ламинарном течении ньютоновской жидкости в зазоре между коаксиальными цилиндрами
Примем во внимание, что для сдвигового течения в зазоре между коаксиальными цилиндрами закон течения ньютоновской жидкости имеет вид [33, 35]:
.
(8.3b)
Подставив профиль скорости течения (8.21) в (8.3b), можно легко получить распределение касательных напряжений τ в зазоре между двумя цилиндрами в случае, когда внутренний цилиндр неподвижен, а внешний вращается со скоростью ωφ (R) = R, где – угловая частота вращения, имеющая размерность [рад/с].
Рассмотрим процесс вывода искомой зависимости касательного напряжения τ = τ(r) от радиальной координаты r. Сначала преобразуем (8.21) к виду
.
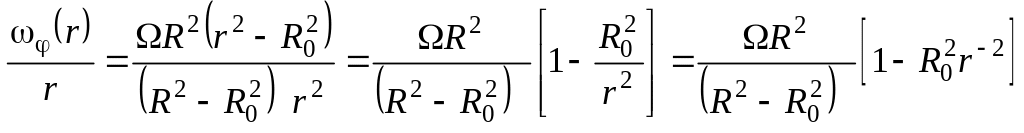После этого вычислим производную
,
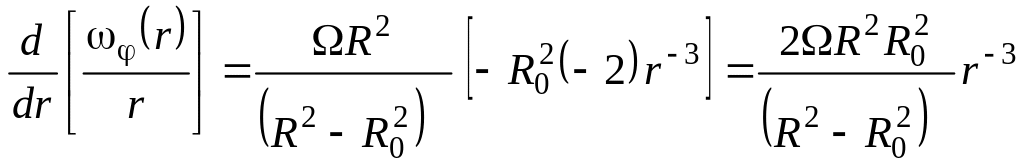а затем получим искомое выражение для вычисления зависимости τ от радиальной координаты r:
.
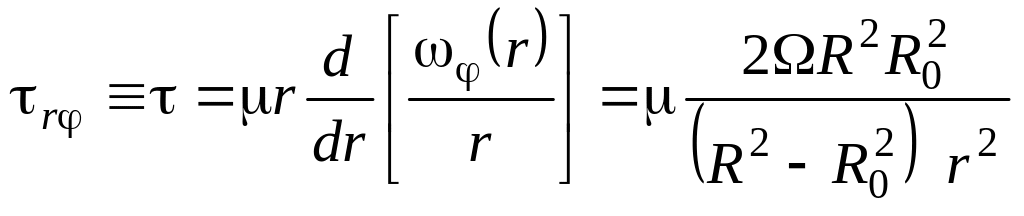(8.22)
Графики, иллюстрирующие распределение профиля скорости ωφ (r) и касательного напряжения (напряжения сдвига) τ(r) по радиальной координате r, построенные по данным табл. 8.1, представлены на рис. 8.5.
8.1 Зависимость ωφ(r) / (R) и τ(r) / τ(R) от отношения r/R при R0 = 0,9R
r / R |
ωφ (r) / (R) |
τ(r) / τ(R) |
0,90 |
0 |
1,1111 |
0,92 |
0,208 |
1,0869 |
0,94 |
0,412 |
1,0638 |
0,96 |
0,612 |
1,0417 |
0,98 |
0,808 |
1,0204 |
1,00 |
1 |
1,0000 |
Рис. 8.5 Зависимость относительной скорости ωφ(r) / (R) и относительного напряжения сдвига τ(r) / τ(R) от радиальной координаты r в зазоре между двумя коаксиальными цилиндрами (внутренний цилиндр неподвижен, а внешний – вращается с постоянной скоростью ωφ(r) = R), рассчитанные по формулам (8.21) и (8.22) при R0 = 0,9R
8.2 Закономерности течения неньютоновских жидкостей
В предыдущем параграфе данной главы были рассмотрены некоторые вопросы течения ньютоновских жидкостей.
Для
ньютоновских жидкостей характерна
независимость динамической вязкости
от скорости сдвига. Благодаря этому
«кривая течения» ньютоновской жидкости
имеет вид прямой линии (см. рис. 8.2),
проходящей через начало координат на
плоскости с координатными осями
.
8.2.1 Примеры неньютоновских моделей текучих систем
При течении неньютоновских жидкостей имеет место существенное отклонение от закона течения Ньютона, обычно записываемого в виде (8.3). Вязкость неньютоновских жидкостей оказывается существенно зависящей от скорости сдвига , а иногда и от времени действия внешней нагрузки. Неньютоновским поведением обладают текучие системы (жидкости), для которых характерно следующее [33]:
силы взаимодействия между молекулами такой текучей системы достаточно велики;
заметная часть молекул такой системы сильно вытянуты (анизодиметричны);
в текучей системе присутствуют взвешенные частицы.