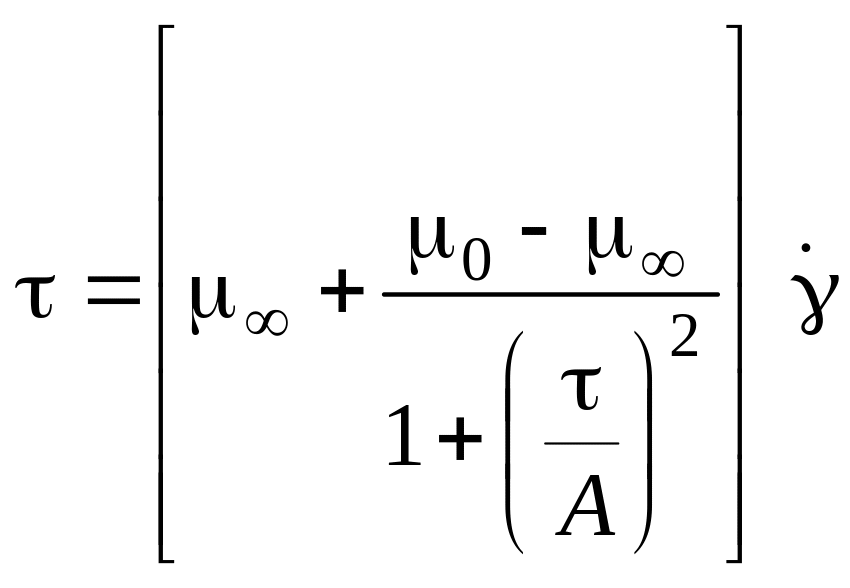- •8 Экспериментальное измерение реологических свойств ньютоновских и неньютоновских жидкостей
- •8.1 Закономерности течения ньютоновских жидкостей
- •8.1.1 Течение Куэтта
- •8.1.2 Ньютоновские жидкости
- •8.1.3 Изотермическое ламинарное движение ньютоновской жидкости в круглой трубе под действием постоянного перепада давления
- •8.1.3.1 Особенности течения ньютоновской жидкости в круглой трубе
- •8.1.3.2 Вычисление профиля скорости установившегося течения ньютоновской жидкости в круглой трубе
- •8.1.3.3 Вычисление средней скорости и расхода ньютоновской жидкости при течении в круглой трубе
- •8.1.3.4 Распределение касательного напряжения по радиусу при течении ньютоновской жидкости в круглой трубе
- •8.1.4.1 Вычисление профиля скорости течения ньютоновской жидкости в зазоре между цилиндрами
- •8.1.4.2 Распределение касательного напряжения по радиусу при установившемся ламинарном течении ньютоновской жидкости в зазоре между коаксиальными цилиндрами
- •8.2 Закономерности течения неньютоновских жидкостей
- •8.2.1 Примеры неньютоновских моделей текучих систем
- •8.2.1.1 Вязкопластичные жидкости Шведова-Бингама
- •8.2.1.1.1 Кривые течения вязкопластичных жидкостей
- •8.2.1.1.2 Коэффициент пластической вязкости жидкости
- •8.2.1.1.3 Кажущаяся вязкость жидкости
- •8.2.1.1.4 Течение вязкопластичной среды Шведова-Бингама в круглой трубе
- •8.2.1.2 Степенное реологическое уравнение состояния
- •8.2.1.2.1 Краткие сведения о реологических свойствах красок
- •8.2.1.2.2 Достоинства и недостатки степенного закона
- •8.2.1.2.3 Течение в круглой трубе неньютоновских жидкостей, подчиняющихся степенному закону Оствальда
- •8.2.1.3 Типичные кривые течения и основные эмпирические модели неньютоновских жидкостей [33]
- •8.1 Основные модели псевдопластичных (нелинейновязких) сред для одноосного сдвигового течения [33]
- •8.2 Основные модели вязкопластичных сред для одноосного сдвигового течения [33]
- •8.3 Методы и устройства для измерения вязкости ньютоновских жидкостей и реологических характеристик реостабильных неньютоновских жидкостей
- •8.3.1 Вискозиметрические приборы, применяемые для контроля показателей качества процессов, продукции, полупродуктов и сырья в промышленности
- •8.3.1.1 Вискозиметрические воронки
- •8.3.1.2 Капиллярные вискозиметры
- •8.3.1.3 Вискозиметры с падающим шариком
- •8.3.1.4 Пузырьковые вискозиметры
- •8.3.1.5 Ротационные вискозиметры
- •8.3.1.6 Недостатки промышленных вискозиметрических приборов
- •Различных неньютоновских жидкостей:
- •8.3.2 Вискозиметрические приборы для научных исследований
- •8.3.2.1 Капиллярные вискозиметры для научных исследований
- •8.3.2.1.1 Устройство капиллярного вискозиметра для научных исследований
- •8.3.2.1.2 Порядок проведения эксперимента с применением капиллярного вискозиметра (рис. 8.12)
- •1 Подготовка капиллярного вискозиметра к проведению эксперимента:
- •2 Проведение эксперимента с целью определения одной точки кривой течения исследуемой жидкости:
- •3 Завершение экспериментов или переход к экспериментальному исследованию новой жидкости:
- •8.3.2.1.3 Методика обработки экспериментальных данных, полученных с помощью капиллярного вискозиметра
- •Вычисление консистентных переменных p и V по экспериментальным данным, полученным с применением капиллярного вискозиметра
- •Вычисление кажущейся, эквивалентной и эффективной вязкостей по данным, полученным с применением капиллярного вискозиметра
- •Методика построения кривой течения для неньютоновских жидкостей по экспериментально определенной зависимости
- •Определение параметров k и n степенного закона Оствальда по данным вискозиметрических измерений
- •8.3.2.2 Ротационные вискозиметры для научных исследований
- •8.3.2.2.1 Ротационные вискозиметры с чувствительным преобразователем типа цилиндр-цилиндр Конструкции ротационных вискозиметров с чувствительным преобразователем в виде пары соосных цилиндров
- •Порядок проведения экспериментов с применением ротационных вискозиметров с преобразователем типа цилиндр-цилиндр
- •1 Подготовка ротационного вискозиметра к работе:
- •2 Проведение эксперимента с целью определения координат точек кривой течения исследуемой жидкости:
- •3 Завершение экспериментов или переход к исследованию новой неньютоновской жидкости:
- •Методика обработки экспериментальных данных, полученных с помощью ротационного вискозиметра с преобразователем типа цилиндр-цилиндр
- •Методика обработки экспериментальных данных, полученных с применением ротационного вискозиметра с чувствительным преобразователем типа диск-конус
8.1 Основные модели псевдопластичных (нелинейновязких) сред для одноосного сдвигового течения [33]
Название модели (закона) |
Формула (уравнение) |
1 Степенной закон |
|
2 Модель Эллиса |
|
3 Модель Сиско |
|
4 Модель Де Хавена |
|
5 Модель Прандтля |
|
6 Модель Уильямса |
|
7 Модель Эйринга |
|
8 Модель Прандтся-Эйринга |
|
9 Модель Пауэлла-Эйринга |
|
10 Модель Рейнера-Филиппова |
|
11 Модель Рабиновича |
|
О
б о з н а ч е н и я:
|
|
Для всех моделей,
приведенных в табл. 8.1, характерны
нелинейные кривые течения, проходящие
через начало координат (![]() ).
).
Большинство таких идеализированных кривых течения не отражают все детали действительного поведения неньютоновских жидкостей во всем возможном диапазоне скоростей сдвига, а передают лишь отдельные наиболее характерные особенности такого поведения.
В табл. 8.1 большинство моделей представлены в квазиньютоновских формах записи:
![]() ;
;
![]() ;
;
![]() .
.
Поэтому коэффициенты при в правых частях формул, приведенных в табл. 8.1, можно трактовать [33] как «кажущиеся коэффициенты динамической вязкости» неньютоновских жидкостей.
В
настоящее время хорошо известно [33], что
все нелинейновязкие псевдопластичные
среды проявляют ньютоновское поведение
при очень малых (
)
и при весьма больших (
)
скоростях сдвига. В каждой из этих
областей среда может быть охарактеризована
постоянными, но различными по величине
кажущимися вязкостями. В первой области
при
наблюдается наибольшая кажущаяся
ньютоновская вязкость, которую обозначают
![]() и обычно называют «вязкость при нулевой
скорости сдвига». Во второй области при
имеет место наименьшая кажущаяся
ньютоновская вязкость, которую обычно
обозначают
и обычно называют «вязкость при нулевой
скорости сдвига». Во второй области при
имеет место наименьшая кажущаяся
ньютоновская вязкость, которую обычно
обозначают
![]() и называют «вязкость при бесконечно
большой скорости сдвига».
и называют «вязкость при бесконечно
большой скорости сдвига».
В табл. 8.2 приведены наиболее часто применяемые на практике модели вязкопластичных сред, характерной особенностью которых является то, что их течение начинается только при напряжении сдвига , превышающем величину предела текучести .
Подробный реологический анализ эмпирических моделей, приведенных в табл. 8.1 и 8.2, рассмотрен в [33].
При выборе той или иной реологической модели при практической работе следует исходить из следующих рекомендаций [33]:
– применяемая реологическая модель должна быть хорошо согласована с теоретическими представлениями о внутренней структуре исследуемой (используемой) среды, а также с изменениями, происходящими в этой структуре как под действием приложенного напряжения сдвига , так и в процессе течения, начинающегося после превышения предела текучести, т.е. при ;
– при прочих равных условиях предпочтение следует отдавать более простой реологической модели, содержащей наименьшее число параметров.