8 Экспериментальное измерение реологических свойств ньютоновских и неньютоновских жидкостей

В настоящее время к теплофизическим свойствам и характеристикам веществ относят порядка 70 физических величин, в число которых, кроме:

• теплопроводности λ,

• удельной теплоемкости с,

• объемной теплоемкости сρ,

• коэффициента температуропроводности ,

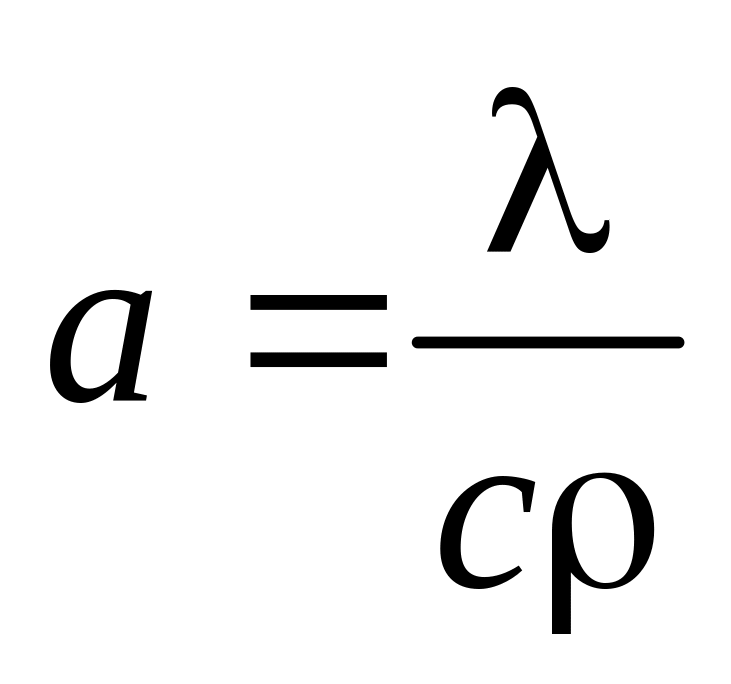• коэффициента тепловой активности ,

входят большое количество и других физических свойств (и характеристик) веществ, например:

• динамическая вязкость μ ньютоновской жидкости;

• кинематическая вязкость ньютоновской жидкости;

• коэффициент линейного расширения α_л;

• коэффициент объемного расширения ;

• коэффициент теплообмена α, являющийся скорее характеристикой процесса теплообмена, нежели свойством вещества;

• показатель консистенции k и индекс течения n, входящие в рассматриваемый ниже степенной закон Отвальда течения неньютоновских жидкостей;

• «кажущаяся» _а, «эквивалентная» μ_экв и «эффективная» μ_эф вязкости неньютоновских жидкостей;

• плотность ρ веществ;

• коэффициент диффузии a_m и т.д.

В данной главе рассматриваются основные вопросы теории и практики измерения реологических свойств, к числу которых относятся динамическая вязкость μ ньютоновских жидкостей; показатель консистенции k и индекс течения n неньютоновских жидкостей; «кажущаяся» _а, «эквивалентная» μ_экв и «эффективная» μ_эф вязкости неньютоновских жидкостей и др.

8.1 Закономерности течения ньютоновских жидкостей

8.1.1 Течение Куэтта

Внутреннее трение (вязкость) любой подвижной (газообразной, жидкой, однородной или дисперсной) среды возникает при ее течении, т.е. при таком движении, которое характеризуется отличными от нуля градиентами скорости [31 – 34]. Простейшим примером такого одноосного сдвигового движения жидкости является так называемое течение Куэтта [33] (см. рис. 8.1). Такое течение возникает в зазоре между двумя пластинами 1 и 2, первая из которых неподвижна, а вторая движется с постоянной скоростью ₀.

Рис. 8.1 Графическая иллюстрация течения Куэтта

Если расстояние между пластинами 1 и 2 равно h, то после достижения установившегося во времени режима течение Куэтта характеризуется линейным профилем скорости [33]:

, (8.1)

где скорость течения вдоль оси z; максимальная скорость течения, совпадающая со скоростью движения пластины 2; x – поперечная координата, направленная перпендикулярно к оси z; H – расстояние между пластинами 1 и 2.

8.1.2 Ньютоновские жидкости

Величина вязкого (внутреннего) трения при сдвиговом течении определяется касательным напряжением , которое требуется приложить к верхней пластине 2 для того, чтобы поддерживать течение с определенным градиентом скорости , имеющим размерность [1/с] и (в случае одноосного сдвигового течения) называемым скоростью сдвига.

Вязкость – это мера интенсивности противодействия возникающих в жидкости сил внутреннего трения F сдвиговому течению этой жидкости. Физическая величина, обычно называемая динамической вязкостью μ, в действительности представляет собой коэффициент, входящий в соотношение

, (8.2)

где F – сила, действующая по касательной к поверхности площадью S; скорость сдвига (градиент скорости в направлении оси x, ориентированной нормально (перпендикулярно) направлению течения); μ – коэффициент, называемый динамической вязкостью; ω_z – компонент вектора скорости в направлении оси z.

Если ввести обозначения:

касательное напряжение (напряжение сдвига), представляющее собой отношение силы F, действующей в направлении оси z на поверхность (ориентированную нормально к оси х), к величине площади S этой поверхности;

скорость сдвига,

то формулу (8.2) можно представить в виде [33]:

. (8.3)

Формула (8.3) выражает так называемый закон течения Ньютона применительно к условиям одноосного (одномерного) сдвига. Жидкости, течение которых подчиняется закону Ньютона (8.3), называют ньютоновскими жидкостями [33].

Кроме ньютоновских жидкостей есть большое количество жидкостей, течение которых не подчиняется закону Ньютона (8.3). Такие жидкости обычно называют неньютоновскими жидкостями [33].

Механическое поведение текучих систем (ньютоновских и неньютоновских) при их сдвиговом течении можно графически представить двумя видами зависимостей [33], приведенными на рис. 8.2.

Рис. 8.2 Графическое представление течения ньютоновских жидкостей:

а – в виде зависимости касательного напряжения сдвига τ от скорости сдвига ;

б – в виде зависимости динамической вязкости μ от скорости сдвига

На рис. 8.2, а показана зависимость касательного напряжения τ от скорости сдвига для ньютоновской жидкости, подчиняющийся закону (8.3). Такой график называют реологической диаграммой или «кривой течения». Коэффициент динамической вязкости μ на такой «кривой течения» неньютоновской жидкости представляет собой тангенс угла наклона прямой линии (8.3).

Другая интерпретация закона течения Ньютона (8.3) представлена на рис. 8.2, б. В этом случае (см. рис. 8.2, б) графически представляется зависимость динамической вязкости μ от скорости сдвига .

Для ньютоновских жидкостей оба варианта графического отображения закономерностей течения представляют собой прямые линии. Поэтому, при изучении течения ньютоновских жидкостей нет основания отдавать предпочтение одному виду графического отображения по сравнению с другим.

Закон Ньютона (8.3) для несжимаемой жидкости (с постоянной плотностью ρ = const) в результате несложных преобразований можно представить в виде [33]:

или

, (8.3а)

где коэффициент кинематической вязкости [м²/с], имеющий ту же размерность, что и коэффициент температуропроводности a и коэффициент диффузии a_m, входящие в законы Фурье и Фика; величина , имеющая физический смысл концентрации количества движения ( ) в единице объема V [м³];  – касательное напряжение сдвига, имеющее размерность [] = = , которое можно интерпретировать как поток количества движения ( ) через единицу поверхности [м²] в единицу времени [с].

Зависимость в виде (8.3а) наиболее отчетливо выявляет аналогию закона Ньютона с другими известными феноменологическими законами переноса субстанции, в частности, с законом теплопроводности Фурье

(8.4)

и законом диффузии Фика

, (8.5)

где q , a , h соответственно тепловой поток q, коэффициент температуропроводности a и объемная энтальпия , имеющая физический смысл концентрации тепловой энергии в единице объема; q_m , a_m , с соответственно поток вещества через единицу поверхности в единицу времени, коэффициент диффузии a_m и концентрация c диффундирующего вещества в единице объема.

Слева в каждом из законов (8.3а), (8.4) и (8.5) стоят потоки (количества движения (m_z), количества тепла Q и количества вещества m) через единицу поверхности в единицу времени, а справа – составляющие градиентов движущих сил, представляющих собой концентрацию переносимой субстанции , , в единице объема V. При этом коэффициент кинематической вязкости , входящий в закон (8.3а), можно трактовать как коэффициент диффузии количества движения (m_z) по аналогии с тем, что коэффициенты a и a_m, входящие в законы Фурье (8.4) и Фика (8.5), обычно рассматривают как коэффициенты диффузии количества тепла Q и количества вещества m. Отметим, что коэффициенты ν, a и a_m, входящие в законы Ньютона (8.3а), Фурье (8.4) и Фика (8.5), имеют одинаковую размерность м²/с.