Добавил:

Kolobok Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уфимский Государственный Авиационный Технический Университет

Предмет:

Теоретические основы электротехники

Файл:

Расчет линейн.электр.цепей пост.тока

.pdf

Скачиваний:

Добавлен:

25.05.2014

Размер:

412.09 Кб

Скачать

☆

1 / 31 2 3 > Следующая >>>

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Южно-Уральский государственный университет Кафедра “Теоретические основы электротехники”

621. 3 (07)

В. Н. Непопалов

Расчет линейных электрических цепей постоянного тока

Методическое руководство по самостоятельной работе студентов

Челябинск

2001

УДК 621.3.011(075.8)

Непопалов В. Н. Расчет линейных электрических цепей постоянного тока: Методическое руководство по самостоятельной работе студентов. – 30 с.

В руководстве поясняются методы расчета линейных электрических цепей постоянного тока. Руководство предназначено в помощь студентам при выполнении и защите семестрового контрольного задания №1 по курсу «Основы электротехники».

Ил. 32, табл. 2.

	ОГЛАВЛЕНИЕ
1.	Метод эквивалентных преобразований............................................................	4
	1.1. Общие сведения................................................................................................	4
	1.2. Решение типовых задач...................................................................................	5
	1.3. Контрольные вопросы и задачи....................................................................	12
2.	Метод узловых напряжений.............................................................................	13
	2.1. Общие сведения..............................................................................................	13
	2.2. Решение типовых задач.................................................................................	14
	3.2. Контрольные вопросы и задачи....................................................................	23

3.Топологические методы формирования математической модели

электрической цепи...................................................................................................	24
3. 1. Общие сведения.............................................................................................	24
3. 2. Решение типовых задач................................................................................	27

1. Метод эквивалентных преобразований

1.1. Общие сведения

Метод эквивалентных преобразований основан на замене двухполюсника одного вида на двухполюсник другого вида.

Двухполюсники на рис. 1.1 будут эквивалентными, если

Rэк = R1 + R2 + K+ Rn .

Rэк

Рис. 1.1 Эквивалентность преобразования двухполюсников на рис. 1.2 определяет

отношение

+K+

эк

В случае n = 2

Rэк

откуда

R =	R1R2 .	Рис. 1.2
эк	R1 + R2	Рис. 1.2
эк

При решение задач часто используется преобразование треугольник– звезда (рис. 1.3).

	1		1		Формулы эквива-
	1			лентныхпреобразований
				лентныхпреобразований
				имеют вид
				R12	R	=	R1R2
R1			R2		R	=	R1R2	,
R1			R2		12		D	,
		R3	R13	R23	R23 =		R2 R3	,
		R3					D
2			3 2	3	R	=	R1R3	,
			Рис. 1.3		13		D	,
			Рис. 1.3	где	D = R1 + R2 + R3 .

Двухполюсники, в которых

б)

есть источники э. д. с. и (или) тока,

называются активными (рис. 1.4).

Рис. 1.4

Рис. 1.5

Двухполюсники на рис. 1.5 эквивалентны, если имеют одинаковые внеш-

ние характеристики U (I ) .

Для двухполюсника по схеме рис. 3, а имеем

U = E − RI .

Внешняя характеристика двухполюсника по схеме рис. 3, б определится

из уравнения

− J + I + GU = 0 ,

откуда

U =

−

I .

Двухполюсники эквивалентны, если

E =

;

R =

1.2. Решение типовых задач

Задача 1.1

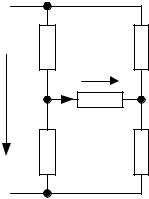
Найти токи в ветвях и напряжение Uab

в цепи

по схеме рис. 1.6.

R21

R31

Напряжение U = 75 B. Параметры цепи:

Uab

R1 = 50 Ом; R21 = 20 Ом; R22 =30 Ом; R31 =30

Ом; R32 = 20 Ом.

R22

R32

Решение

Определяем положительные направления то-

ков ветвей (рис. 1.6).

Рис. 1.6

В ветвях с токами I2

и I3 резисторы R21, R22 и

R31, R32 соединены последовательно. Следовательно,

R2 = R21 + R22 = 50 Ом;

R3 = R31 + R32 = 50 Ом.

Участки R2, R3 соединены параллельно, поэтому

R =	R2 R3		=	50 50	= 25 Ом.

23	R2	+ R3	50 + 50

Электрическую цепь, состоящую из двух последовательно соединенных резисторов, называют делителем напряжения.

Рассчитываем делитель напряжения R1, R23.

Токи и напряжения делителя определяются по выражениям:

I1	=		U	=	75	= 1 А;
		R1	+ R23		50 + 25

U1 = I1R1 = 1 50 = 50 В;

U2 = I1R23 = 1 25 = 25 В;


I2	=		U2	=	25	= 0,5	A;
			R2		50

I3	=	U2		=	25	= 0,5	A.
					50
			R3

Напряжение Uab находим по второму закону Кирхгофа

Uab = I2 R22 − I3R32 .

Получаем

Uab = 0,5 30 – 0,5 20 = 5 B.

Задача 1.2

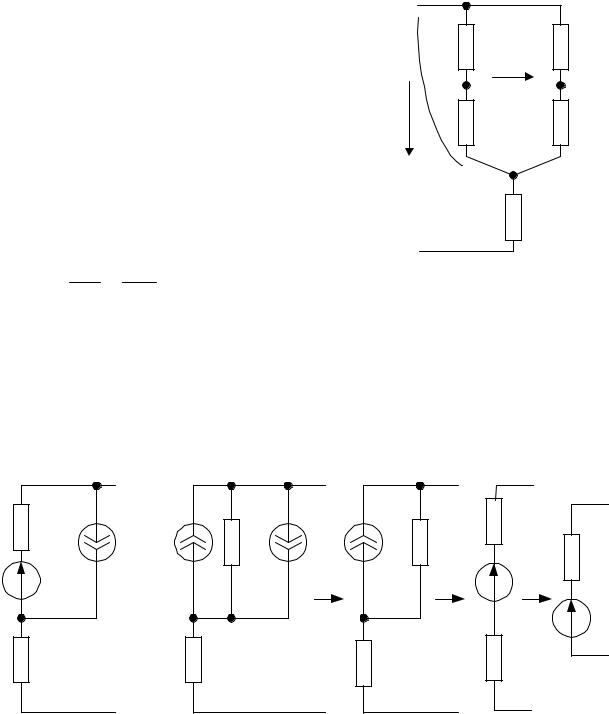
Найти ток в ветви a – b цепи по схеме рис. 1.7. Параметры цепи: R1 = 47 Ом; R2 = 75 Ом; R3 =33 Ом; R4 = 25 Ом; R5 = 40 Ом. Напряжение U = 100 В.

Решение

Определяем положительное направление тока I ветви a – b. Преобразуем треугольник из резисторов R3,

R4, R5 в звезду R35, R45, R34.

По формулам эквивалентных преобразований имеем:

D = R3 + R4 + R5 = 33 + 25 + 40 = 98 Ом;

R3 R4

33 25

= 8,42 Ом;

R4 R5

25 40

= 10,2 Ом;

R3 R5

33 40

= 13,47 Ом.

Получаем схему замещения (рис. 1.8).

1
R1 Uab	R2
U a I	b
R5
R3	R4

Рис. 1.7

Определяем эквивалентные сопротивления последовательно и параллельно соединенных участков:

R135 = R1 + R35 = 60,47 Ом;

R245 = R2 + R45 = 85,2 Ом;

R135 R245

60,47 85,2

= 35,7 Ом.

R135 + R245

60,47 + 85,2

Рассчитываем делитель напряжения R10,

R34. Напряжение

U10

UR10

100 35,7

R10

+ R34

35,7 + 8,42

= 80,92 B.

Рассчитываем делители R1 – R35; R2 – R45 и

определяем

R35

R45

= U

−

= 8,32B.

135

245

Ток в ветви a – b находим по закону Ома:

I = Uab = 8,32 = 0,208 A. R5 40

	R1	R2
	Uab	b
	a	b
U	R35	R45
U

U10 0

R34

Рис.1.8

Задача 1. 3

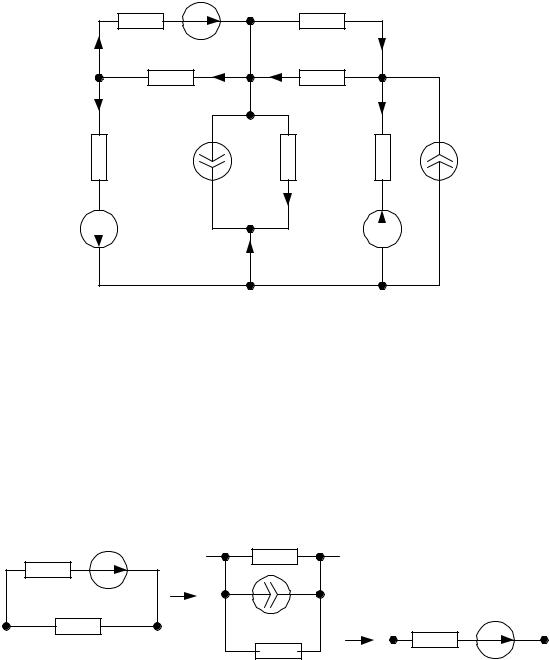
Выполнить эквивалентные преобразования для двухполюсника (схема рис. 1.9). Параметры резисторов двухполюсника: R1 =75 Ом; R2 =50 Ом.

Источники: Е1 = 30 В; J1 = 1 А.

Решение

Этапы выполнения преобразований поясняет рис. 1.10.

R1		R1			R1	R1	R
		R1			R1	E
E1	J1	JE1	J1	J

							E
							E
R2		R		R2		R2
		2
Рис. 1.9.				Рис. 1.10.

Расчет выполняем по формулам эквивалентных преобразований:

JE1 = E1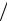R1 = 3075 = 0,4 А;

J = JE1 − J1 = – 0,6 А;

E = JR1 = – 0,6 75 = – 45 В;

R = R1 + R2 = 125 Ом.

Задача 1.4

Методом эквивалентных преобразований рассчитать токи ветвей в цепи со схемой рис. 1.11.

R1		E1		R3
I1	R2	I2	I4	I3

1				R4
			2	3

I5				I7

R5		R6	R7
J6		I6	J7
E5		I6
E5		′	E7
		′	E7
	0	I6
	0

Рис. 1.11

Параметры резисторов ветвей: R1 = 100 Ом; R2 =130 Ом; R3 = 43 Ом; R4 =75

Ом; R5 = 91 Ом; R6 =110 Ом; R7 =200 Ом; R8 = 45 Ом. Источники: Е1 =15 В; Е5 = 24 В; Е7 = 8 В; J6 = 0,2 А, J7 =0,1 А.

Решение

Назначаем положительные направления токов в ветвях. Узлы схемы отмечаем цифрами 1, 2, 3 и 0.

Выполняем эквивалентные преобразования для двухполюсника между узлами

1–2 (рис. 1.12).

R1	E1	R1
R1	E1	1	2
	R2	1	2
	R2	J1	1	R	E12	2
1	2	J1		R	E12
1	2	R2		12
		Рис. 1.12

Находим:

= 0,15 А;

100

100 130

R12

R1R2

= 56,52 Ом;

+ R2

100

+ 130

E12

= J1R12 = 8,48 В.

Между узлами 2– 3 резисторы соединены параллельно, поэтому

R	=	R3 R4	= 43 75	= 27,33 Ом.
34		R3 + R4	43 + 75
		R3 + R4	43 + 75
Получаем схему рис. 1.13.
			R12	E	R34
		1		12
		1		2	3
					3
		I5			I7
		I5			I7

R5		R6	R7
J6		U30	J7
E5		I6
E5		′	E7
			E7

	0	I6
	0

Рис. 1.13 Преобразования для двухполюсника между узлами 3–0 поясняет рис. 1.14.

3	3
3	R7	JE7		3
	R7	JE7	J7	3
			J7	′
R7	0			E7
R7	0
	J7	3	′
			′
		R7	J7	R7
E7				R7

				0
0		0		0

Рис. 1.14

Находим:

J E7	=	E7	=	8	= 0,04 А;
		R7		200

′	= J E7 + J 7		= 0,04 + 0,1		= 0,14 А;
J7	= J E7 + J 7		= 0,04 + 0,1		= 0,14 А;
′	′	= 0,14 200		= 28 В.
E7	= J7 R7	= 0,14 200		= 28 В.
Получаем эквивалентную схему рис. 1.15.
		1	R12		E12	2	R34	3
		1					U23	3
			I5	U21			U23	I30
			I5	U21				I30

R125

U20

U30

′

Рис. 1.15

Ветви на участках 2–1; 1– 0 соединены последовательно. Сопротивление

R125

= R12 + R5

= 56,52 + 91 = 147, 52 Ом.

Э. д. с.

E125

= E12 − E5

= 8,48 – 24 = – 15,52 В.

Ветви на участках 2–3, 3– 0 соединены последовательно. Сопротивление

R347

= R34 + R7

= 27,33 + 200 = 227,33 Ом.

Получаем двухполюсник с двумя узлами (рис. 1.16).

Рассчитываем напряжение U20.

Имеем уравнение:

G U

= J

где G22 =

– собст-

R125

U20

125

347

венная проводимостей ветвей, при-

надлежащих узлу 2;

E′

′

J22 =

E125

− J6 +

– узловой ток.

125

R125

′

Подставляя данные:

G22

= 0,02 1/ Ом,

Рис. 1.16

J22

= – 0,182 А.

Напряжение

J22

− 0,182

U20

= – 8,982

В.

0,02

G22

1 / 31 2 3 > Следующая >>>

Соседние файлы в предмете Теоретические основы электротехники

#
25.05.20143.82 Mб41КОНСПЕКТ ЛЕКЦИЙ по ТОЭ.doc
#
25.05.2014264.7 Кб36Методичка по семинарам 1.doc
#
25.05.2014430.08 Кб14Методичка по семинарам 2.doc
#
25.05.2014769.54 Кб32Методы расчета электрических цепей, содержащих четырехполюсники и управляемые элементы,Фатхеев.doc
#
25.05.20146.96 Mб76Ответы на экзаменационные вопросы.doc
#
25.05.2014412.09 Кб23Расчет линейн.электр.цепей пост.тока.pdf
#
25.05.2014829.16 Кб23Расчет линейных электрич. цепей перем.тока.pdf
#
25.05.201487.55 Кб60Расчет электрических цепей однофазного синусоидального тока. Вариант 11.DOC
#
25.05.201495.23 Кб23ргр №1.doc
#
25.05.2014246.78 Кб29РГР3 ЭСиС.doc
#
25.05.2014378.88 Кб16РГР№1. Чечулина.doc