7.6 Анализ четырёхполюсников с помощью вторичных параметров ()

Напомним, что вторичными параметрами четырёхполюсника являются характеристическое сопротивление и постоянная передачи.

В случаях, когда исследуемый пассивный четырёхполюсник является симметричным, бывает целесообразным воспользоваться уравнениями, в которых токи и напряжения связаны между собой при помощи вторичных параметров.

Для составления таких уравнений выразим коэффициенты матрицы А (A , B, C, D) через вторичные параметры.

Было записано, что

тогда

откуда . (7.21)

Если записать , то

Так как , умножив обе части этого равенства на, запишем:

. (7.22)

Если обе части равенства умножить на, то получим:

. (7.23)

Так как четырёхполюсник симметричный, то

. (7.24)

Подставив найденные коэффициенты в систему уравнений 7.1 запишем А – форму через вторичные параметры:

; (7.25)

. (7.26)

7.7 Линейные и круговые диаграммы (годографы)

7.7.1 Линейные диаграммы

При исследовании электрических цепей часто бывает, что какая-либо комплексная величина определяется уравнением вида:

; (7.27)

где

- изменяющаяся комплексная величина с неизменным аргументом и переменным модулем с (). Геометрически величинапредставляет собой сумму двух векторов в комплексной плоскости, один из которых постоянен -, а другого -неизменным остаётся направление, но изменяется длина. Для пояснения рассмотрим электрическую цепь, состоящую из двух последовательно соединённых приёмников (рис. 7.9).

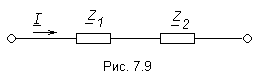
Пусть

такое, что , а- изменяется. Комплексное сопротивление всей цепи

И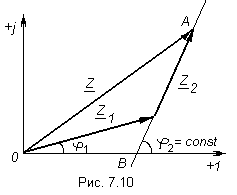зобразим его на комплексной плоскости (рис. 7.10).

Модуль сопротивления изменяется по линии АВ при неизменном аргументе. Прямую АВ называютлинией переменного параметра.

7.7.2 Круговые диаграммы четырёхполюсников

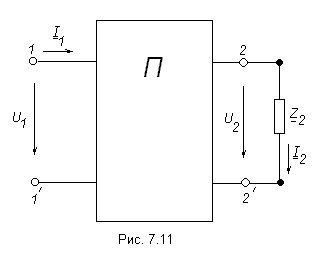
Рассмотрим схему с четырёхполюсником на рис. 7.11.

В четырёхполюснике зависимость между входным и выходным токами имеет линейный характер.

, (7.28)

где и- комплексные числа.

Определим эти коэффициенты.

Если ветвь разомкнута (нагрузкаотключена - режим холостого хода), тои. Подставив эти значения в уравнение 7.28, запишем:.

Если же ветвь замкнута накоротко (режим короткого замыкания), тои. Поэтому

. (7.29)

Отсюда выразим коэффициент :

. (7.30)

Подставив 7.30 и 7.29 в 7.28, получим:

. (7.31)

Если подать питание со стороны зажимов , то при коротком замыкании ветвиполучим ток:

, (7.32)

где

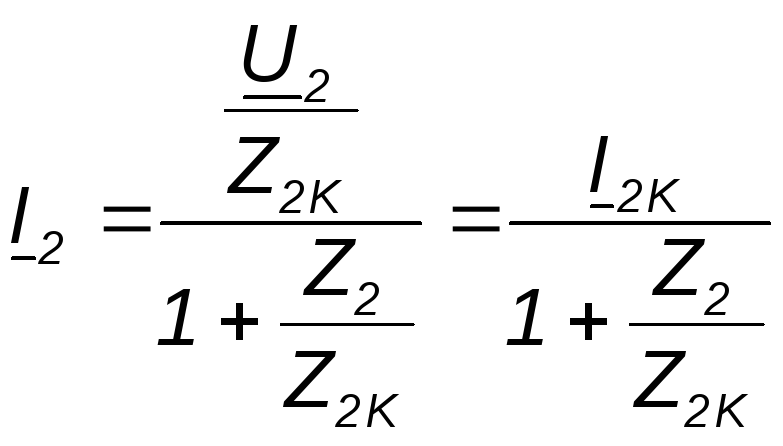
Откуда

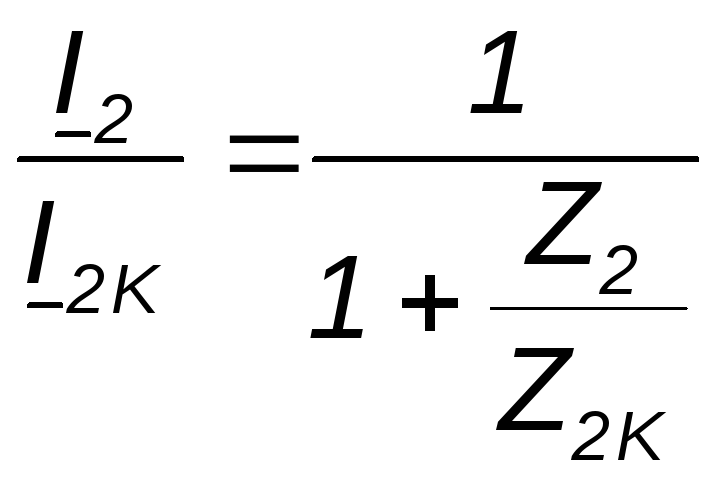. (7.33)

Подставив 7.33 в 7.31 , запишем следующее:

, (7.34)

где

Для построения кривой диаграммы можно воспользоваться следующей последовательностью:

1. Откладываем вектор 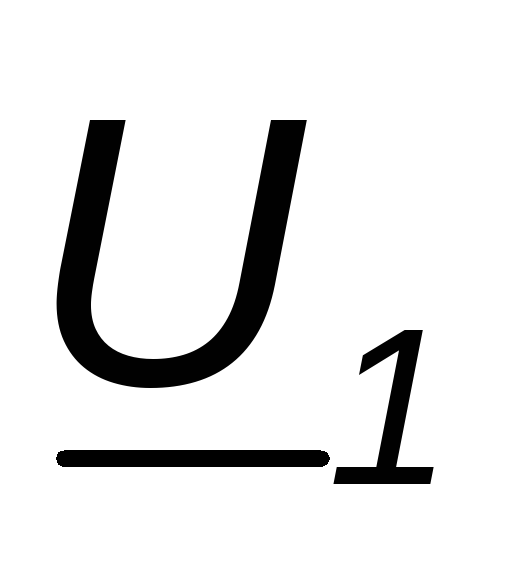в соответствующем масштабе. На диаграмме направляем вдоль оси +1 (примем направление оси +1 вверх).

2. Определяем ток 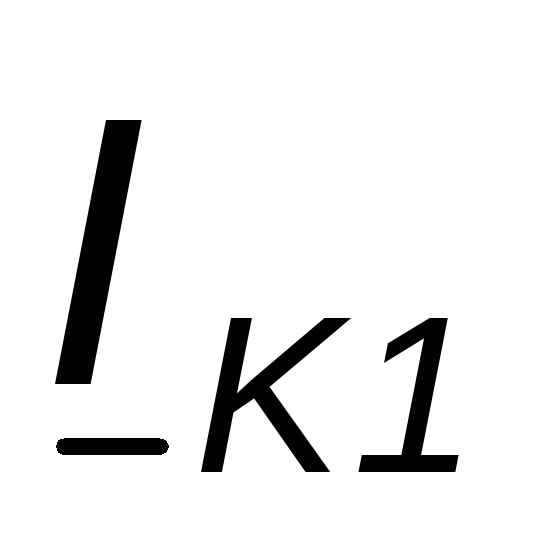при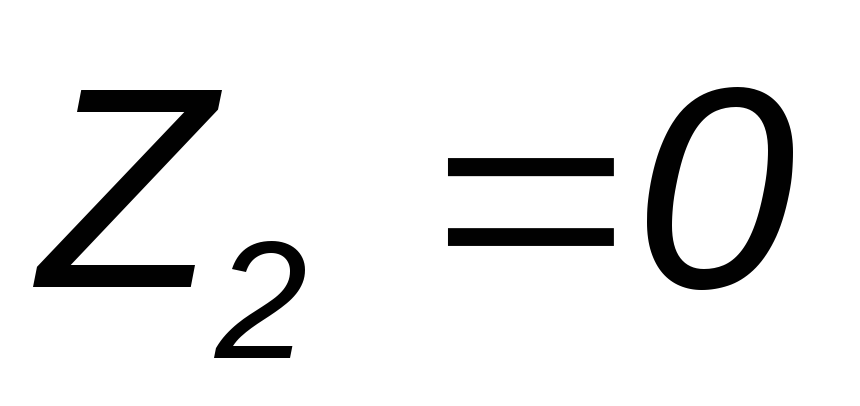, то есть при коротком замыкании на выводах приёмника.

3. Выбираем масштаб для тока и откладываем вектор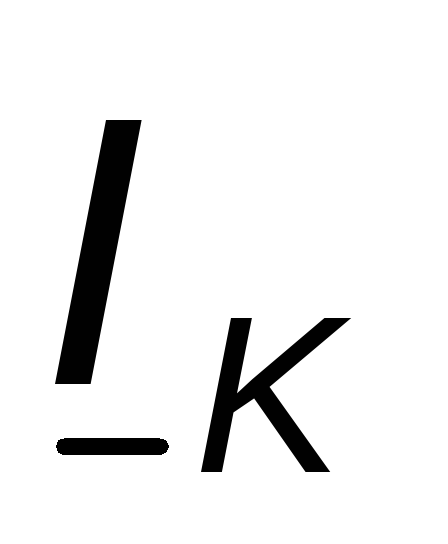(отрезок ОК на диаграмме) (примем для определённости ток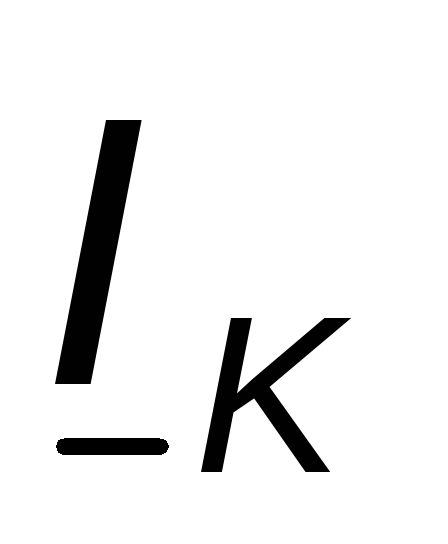отстающим от напряжения ).

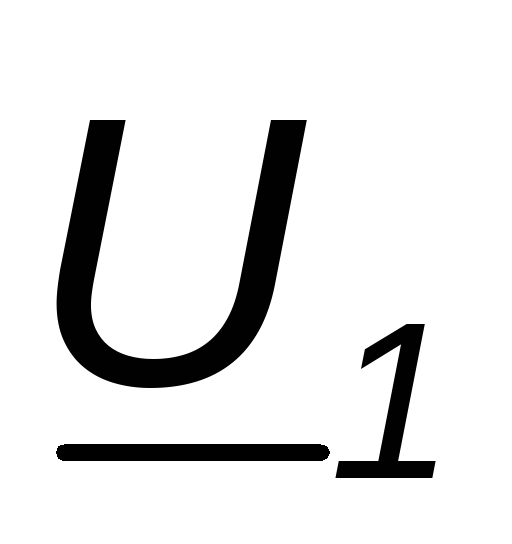4. На отрезке ОК откладываем сопротивление 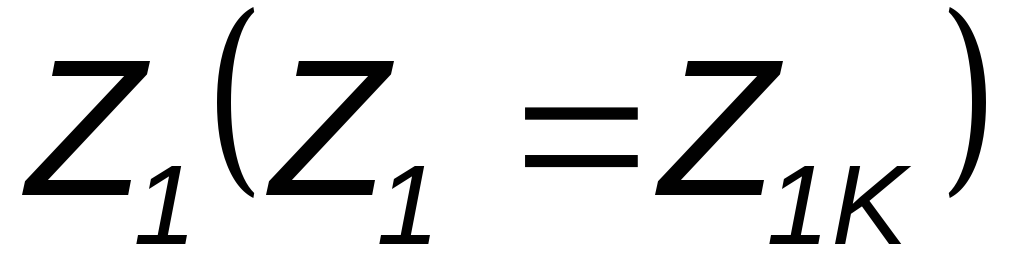в масштабе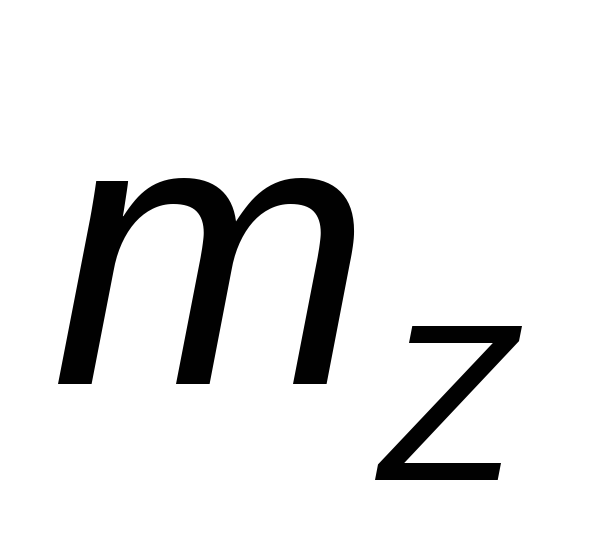(на диаграмме).

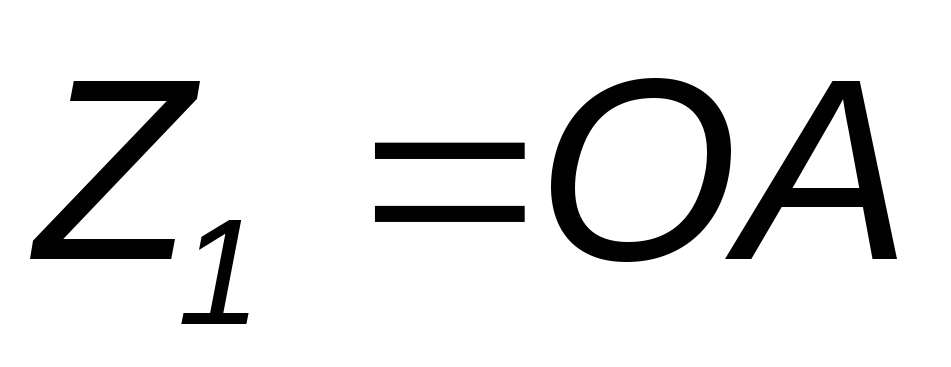5. Из точки А под углом -(так принято) к вектору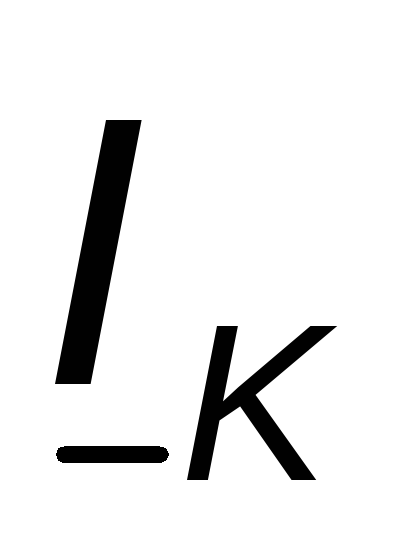проводим линию переменного параметра АВ (Л.П.П.). Для определённости предположим, что, то есть

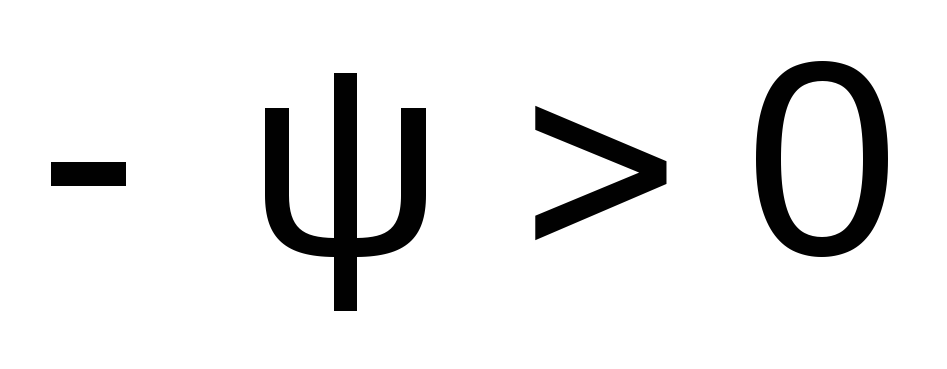
6. Из начала координат проводим прямую OD перпендикулярно АВ.

7. Находим центр С кривой диаграммы как точку пересечения прямой OD и перпендикуляра, восставленного в середине хорды ОК.

8. Циркулем проводим дугу диаграммы, ограниченную хордой ОК.

Пример круговой диаграммы предоставлен на рис. 7.12.