В конце материала информация!

Геометрические преобразования, реализуемые матрицей 2х2

У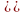 множим вектор-строку || х у ||, определяющую точку Р, на матрицу преобразования 2х2 общего вида: т.е. исходная точка P(х, у) преобразуется в точку P*(х*, у*), где х*=(ах+су), а у*=(bх+dy).

Проведем анализ этого преобразования, рассмотрев частные случаи:

b, c = 0
a, d > 0	Масштабирование (ax dy)
a, d > 1	Масштаб увеличения
0< a, d <1	Масштаб уменьшения
a = d > 0	Пропорциональное масштабирование по осям
a ≠ d > 0	Непропорциональное масштабирование по осям
a, d < 0	Отображение с масштабированием
a, d = -1	Отображение относительно начала координат
a=-1, d=1	Отображение относительно оси Y
a=1, d=-1	Отображение относительно оси X
a= d = 1	Пустой оператор
а= d = 1
b, c ≠ 0	Сдвиг относительно осей X и Y
b=0, c ≠ 0	Сдвиг относительно оси Y
b≠0, c=0	Сдвиг относительно оси X
a= d = cos α; b=sin α; c=-sin α	Поворот на угол α относит. начала координат

Представление прямых линий

Прямая линия может быть задана двумя векторами положения, определяющими координаты ее двух точек. Выбор типа операции проведения линии между двумя точками будет зависеть от типа выходного графического устройства.

Пусть имеется прямая линия, заданная вектором положения || 0 1 || точки А и вектором положения || 2 3 || точки В, и задана матрица преобразования

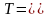, которая осуществляет операцию сдвига точки.

Используя умножение матрицы преобразования на векторы положения точек А и В, получим новые преобразованные векторы А* и В*:

.

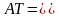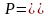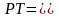Таким образом, элементами А* являются х* = 3 и y*= 1, а для В* - x*=11, y*=7. Более компактно прямая линия, проходящая через точки А и В, может быть представлена матрицей вида , где первая строка является вектором положения точки А, а вторая строка - вектором положения точки В. После умножения P на Т получим . Компоненты матрицы P* представляют собой преобразованные векторы положения точек А* и В*. Легко видеть, что операция сдвига увеличила длину линии и изменила ее положение. В рассмотренном примере мы трансформировали прямую линию у= х+1 между точками А и В в прямую линию у^* = (3/4)х^* - (5/4) между точками А* и В*. Выполненная операция справедлива для любой исходной линии и обеспечивает взаимно однозначное соответствие между точками исходной линии и точками на преобразованной линии. Это означает, что положение любой прямой линии может быть преобразовано в любое новое положение простым преобразованием ее граничных точек с последующим проведении линии между преобразованными точками.

Таким образом, каждая точка прямой взаимно одназначно преобразуется с помощью процедуры перемножения матриц в некоторую другую прямую в той же системе координат, а параллельные прямые с помощью тех же операций преобразуются в параллельные прямые. Следовательно, любую фигуру с помощью операции перемножения матриц можно преобразовать в изоморфную фигуру в той же системе координат относительно ее начала.