Нестационарные модели.

Класс моделей, для которых -я разность является стационарной (среднее постоянно, а выборочные дисперсия и автокорреляция не меняются во времени) называется смешанным процессом авторегрессии и проинтегрированного скользящего среднего (ARIMA).

Берутся разности ряда столько раз, пока полученный ряд не станет стационарным. Количество разностей определяется параметром . Для стабилизации дисперсии применяют логарифмическое преобразование.

После взятия первых разностей устраняют линейный тренд, а второе взятие разностей устраняет квадратичный тренд. На графике, в первом случае до взятия разностей, исходный ряд может иметь резкие колебания, которые имеют линейную тенденцию изменения без резких изменений наклона, если же в исходном ряде наблюдается резкое изменение наклона уровней ряда, то необходимо применить последовательно и взятие первых и вторых разностей. Если в исследуемом ряду присутствует сезонная компонента, то требуется взятие соответствующей сезонной разности.

Нестационарность процесса можно идентифицировать и с помощью коррелограммы.

Коррелограмма – это графическое представление выборочных коэффициентов автокорреляционной функции (АКФ) и их стандартных ошибок для последовательности задержек . На графике приводится ширина интервала в размере двух стандартных ошибок при каждой задержке.

Нестационарность процесса можно идентифицировать по отсутствию быстрого спада выборочной АКФ и необязательно, чтобы АКФ были велики при малых задержках. Необходимый порядок разности считается достигнутым, если АКФ быстро затухает.

Приведем наиболее часто встречающие модели – ARIMA(0,1,1), ARIMA(1,1,0), ARIMA(1,1,1), ARIMA(0,2,2):

- модель ARIMA(1,d,0) – АКФ – экспоненциально затухает, ЧАКФ – только .

- модель ARIMA(0,d,1) – АКФ – только , ЧАКФ – экспоненциально затухает.

- модель ARIMA(2,d,0) – АКФ – имеет форму затухающей синусоиды или экспоненциально убывает. ЧАКФ – только и .

- модель ARIMA(0,d,2) – АКФ – только и , ЧАКФ – имеет форму затухающей синусоиды или экспоненциально убывает.

- модель ARIMA(1,d,1) – АКФ и ЧАКФ – экспоненциально затухают при .

- модель ARIMA(p,d,q)(ps,ds,qs) – мультипликативная сезонная модель авторегрессии и проинтегрированного скользящего среднего.

В дополнение к несезонным параметрам в модель вводятся сезонные параметры для определения задержки, устанавливаемой на этапе идентификации порядка модели. Аналогично параметрам простой модели АРПСС, эти параметры называются: сезонная авторегрессия , сезонная разность и сезонное скользящее среднее .

Например, модель (1,1,2)(0,1,1) включает 1 параметр авторегрессии , 2 параметра скользящего среднего и 1 параметр сезонного скользящего среднего . Эти параметры вычисляются для ряда , определяемого следующим образом. Получают ряд после взятия первой разности с задержкой . Далее берут сезонные разности в ряде следующим образом: . Сезонная разность, используется для сезонных параметров и определяется на этапе идентификации порядка модели.

Например, сезонная разность при временных интервалах равных месяцу и при временных интервалах равных кварталу. Общие рекомендации относительно выбора , , с помощью АКФ и ЧАКФ применимы и к сезонным моделям.

Область применения рассмотренных моделей может быть существенно расширена, если использовать нелинейное преобразование, например, .

Начальные оценки параметров авторегрессии.

Для оценки параметров авторегрессии порядка можно использовать уравнение Юла-Уокера .

; .

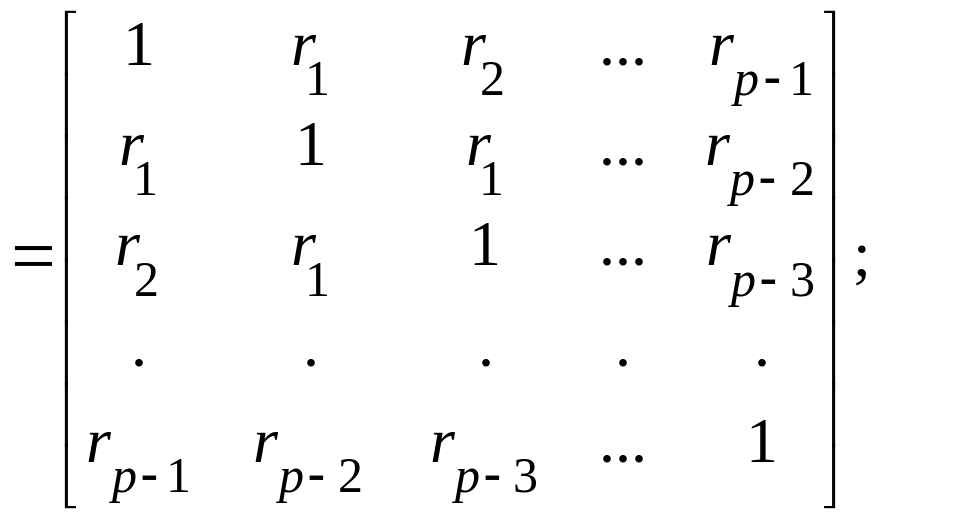
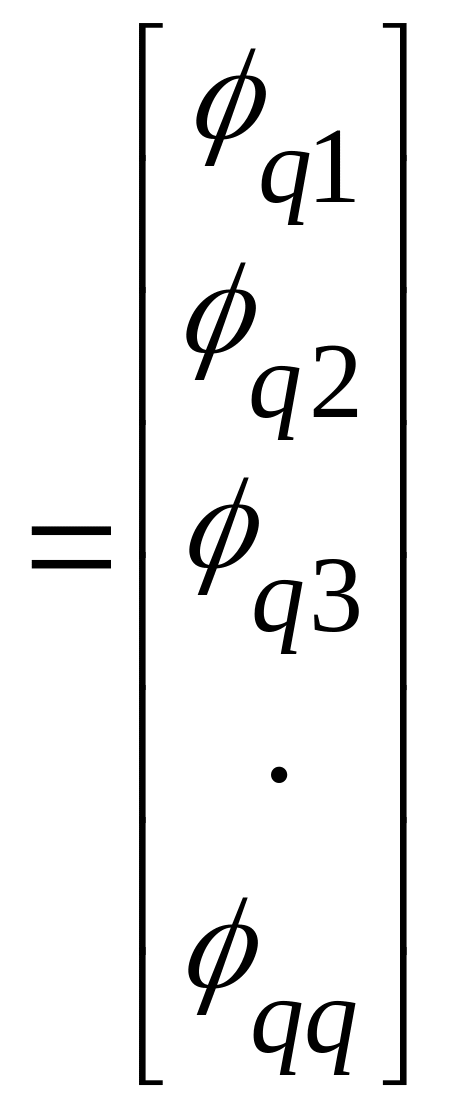Параметры модели авторегрессии при достаточно большом близки к эффективным оценкам максимального правдоподобия.

Начальные оценки параметров скользящего среднего.

Введем обозначение ώ_t и будем анализировать процесс ώ_t, как процесс скользящего среднего ώ_t . Выразим автоковариацию процесса ώ_t через автоковариации процесса

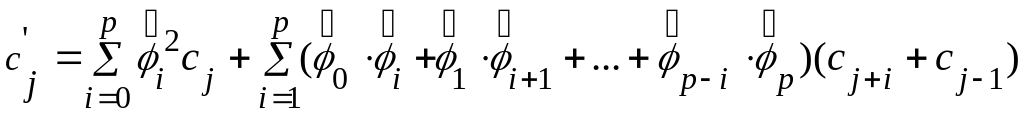, где .

Используя полученные автоковариации , можно получить начальные оценки параметров скользящего среднего для ряда ώ_t при помощи итерационного процесса

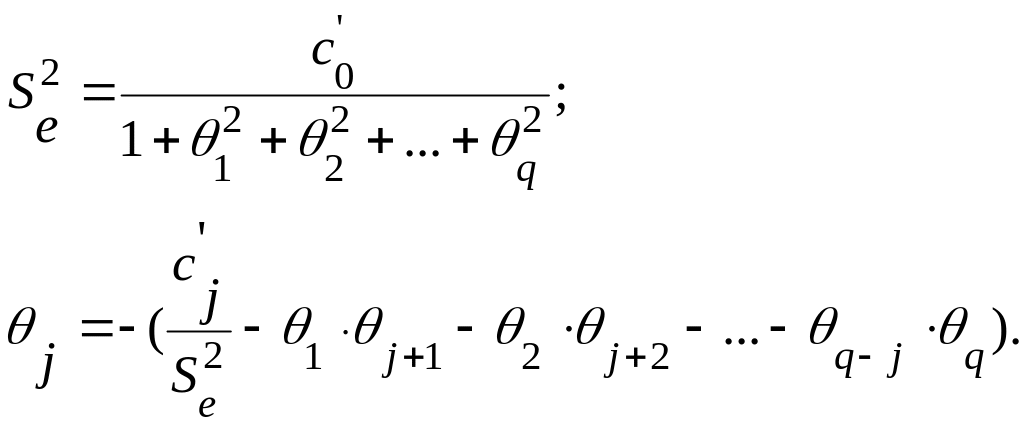
Параметры , , …, в начале первой итерации приравниваются к нулю, а затем полученные значения и используют для последующих вычислений, пока не сойдутся с заданной точностью.

Как было отмечено выше, порядок и не превыщает двух, поэтому рассмотрим оценки параметров авторегрессии и скользящего среднего в явном виде для и первого и второго порядка.

Модель ARIMA(1,d,1);

, для 1-й итерации .

Для стационарного процесса в модели первого порядка необходимо выполнение следующих условий: и .

Модель ARIMA(2,d,2);

, для 1-й итерации .

Для стационарного процесса в модели второго порядка необходимо, чтобы выполнялись следующие условия:

; ; ; ; ; .

Модель AR(1,d,0). , где . Дисперсия процесса определяется S_ỹ² ; ;

Оценка ; и .

Модель AR(2,d,0); + + ; S_ỹ² ;

; ; ; ; .

Модель MA(0,d,1); ; ;

; ; ; ;

.

После оценки параметров модели необходимо проверить ее надежность. Хорошо подогнанная модель не должна иметь зависимые остатки. Зависимость может быть обнаружена из анализа графика остатков и анализа автокорреляционных функций остатков модели.

Пример 2.6. Рассмотрим по небольшому объему выборочных данных методику выбора типа модели, получение оценок параметров модели, оценки ее надежности и способа получения прогнозов. Пусть имеем следующие наблюдения урожайности зерновых по годам:

9,5 13,7 12,1 14,0 13,2 15,6 15,4 14,0 17,6 15,4 10,9 17,5 15,0 18,5 14,2 14,9

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

Для уменьшения вариации исследуемого процесса исходный временной ряд прологарифмируем и проверим на стационарность. Если полученный ряд стационарен, то приступаем к выбору типа модели по описанной выше методике. Если ряд не стационарен, то берем первые разности и последующие, пока ряд не станет стационарным. Все необходимые расчеты сведем в табл. 2.10.

Как видно из табл. 2.10 ряд не стационарен и только после взятия первых разностей расчетное значение критерия серий не попадает в критические области с доверительной вероятностью равной 0,95 ( и ) при .

Таблица 2.10

			Î		Î
1	9,5	2,251	0	0,366	13	0,336	-0,154	0,116	-0,052	0,039	0,113
2	13,7	2,617	3	-0,124	4	-0,154	0,116	-0,089	-0,018	0,014	0,024
3	12,1	2,493	1	0,146	8	0,116	-0,089	0,137	-0,010	0,016	0,013
4	14,0	2,639	2	-0,059	5	-0,089	0,137	-0,043	-0,012	0,004	0,008
5	13,2	2,580	1	0,167	7	0,137	-0,043	-0,125	-0,006	-0,017	0,019
6	15,6	2,747	7	-0,013	5	-0,043	-0,125	0,199	0,005	-0,008	0,002
7	15,4	2,734	5	-0,095	4	-0,125	0,199	-0,164	-0,025	0,020	0,016
8	14,0	2,639	1	0,229	6	0,199	-0,164	-0,376	-0,032	-0,075	0,040
9	17,6	2,868	6	-0,134	3	-0,164	-0,376	0,443	0,061	-0,072	0,027
10	15,4	2,734	4	-0,346	0	-0,376	0,443	-0,184	-0,167	0,069	0,141
11	10,9	2,389	0	0,473	4	0,443	-0,184	0,180	-0,082	0,080	0,197
12	17,5	2,862	3	-0,154	1	-0,184	0,180	-0,295	-0,033	0,054	0,034
13	15,0	2,708	2	0,210	2	0,180	-0,295	0,018	-0,053	0,003	0,032
14	18,5	2,918	2	-0,265	0	-0.295	0,018		-0,005		0,087
15	14,2	2,653	0	0,048	0	0,018					0,000
16	14,9	2,701	0
∑			37	0,450	62				-0,428	0,126	0,752

Для того чтобы выбрать тип модели необходимо рассмотреть поведение АКФ и ЧАКФ. Так как исследуемый ряд имеет небольшое количество наблюдаемых данных, то исследуем поведение АКФ и ЧАКФ при задержке . Расчетные значения этих характеристик и их стандартные ошибки приведены в табл. 2.11 и представлены графически (рис. 2.9, рис. 2.10).

Таблица 2.11

: Урожайность зерновых по годам; ln(x), D(1)

k	ck	rk	se	p-уровень
0	0,0501	1
1	-0,0286	-0,5697	0,2343	0,0150
2	0,0084	0,1680	0,2258	0,0394
3	-0,0031	-0,0621	0,2169	0,0878
4	0,0007	0,0150	0,2077	0,1615

Рис. 2.9. АКФ

Р ис. 2.10. ЧАКФ

Как видно из графиков АКФ и ЧАКФ – экспоненциально затухают и неотличимы от нуля, при задержке . Отличны от нуля только АКФ и ЧАКФ при задержке , следовательно, порядок авторегрессии будет равен и скользящего среднего . Так как ряд стационарен при задержке , то данный процесс может быть описан моделью ARIMA(1,1,1). Данную модель можно записать следующим образом , где ω_t = .

Представим полученную модель в разностном виде:

;

;

;

.

…

При прогнозировании в момент времени .

Тогда ; .

В этой модели нужно определить параметры ₁ и . Их можно определить так:

;

для 1-й итерации .

Итерации
0	-	0
1	0,037632	0,366049
2	0,033185	0,415096
3	0,032101	0,429121
-------------------------------------------------------------------------------------------------------------
7	0,031638	0,435396
8	0,031635	0,435441

Итерационный процесс сошелся на 8-й итерации с точностью 0,0001. Коэффициенты модели удовлетворяют условию стационарности. Так как хорошо подогнанная модель не должна иметь зависимые остатки, но такое заключение можно сделать, имея достаточный объем наблюдений, как уже отмечалось не менее 50. Эта зависимость может быть обнаружена из анализа графика остатков (рис. 2.11, 2.12). Анализ автокорреляционных функций остатков модели говорит о том, что автокорреляции остатков малы и не отличаются от нуля.

Рис. 2.11

Рис. 2.12

Прогнозные данные получим, используя модель в разностном представлении (табл. 2.12).

Таблица 2.12

1	9,5	2,2513	-	-	-
2	13,7	2,6174	-	-	-
3	12,1	2,4932	2,5095	-0,0163	12,3
4	14,0	2,6391	2,5369	0,1022	12,6
5	13,2	2,5802	2,5516	0,0286	12,8
6	15,6	2,7473	2,5851	0,1622	13,3
7	15,4	2,7344	2,6274	0,1070	13,8
8	14,0	2,6391	2,6916	-0,0525	14,8
9	17,6	2,8679	2,6900	0,1779	14,7
10	15,4	2,7344	2,7230	0,0114	15,2
11	10,9	2,3888	2,7688	-0,3800	15,9
12	17,5	2,8622	2,6561	0,2061	14,2
13	15,0	2,7081	2,6329	0,0752	13,9
14	18,5	2,9178	2,7208	0,1970	15,2
15	14,2	2,6532	2,7702	-0,1169	16,0
16	14,9	2,7014	2,7821	-0,0808	16,2
17			2,8138		16,7
18			2,8044		16,5

Например:

.

;

;

;

;

………………………………………………………………………..;

;

;

.

Пример 2.7. Рассмотрим временной ряд, содержащий сезонную компоненту. Имеются данные об объеме розничных продаж по месяцам за три года.

1 2 3 4 5 6 7 8 9 10

92,4 93,2 103,8 104,1 111,2 111,7 106,3 110,6 103,4 109,0

11 12 13 14 15 16 17 18 19 20

112,7 130,9 98,8 95,6 110,2 113,2 120,5 115,1 115,8 121,4

21 22 23 24 25 26 27 28 29 30

114,5 116,5 118,7 139,3 106,7 100,4 114,9 116,3 126,1 121,0

31 32 33 34 35 36

121,4 124,7 125,4 123,8 121,4 152,1

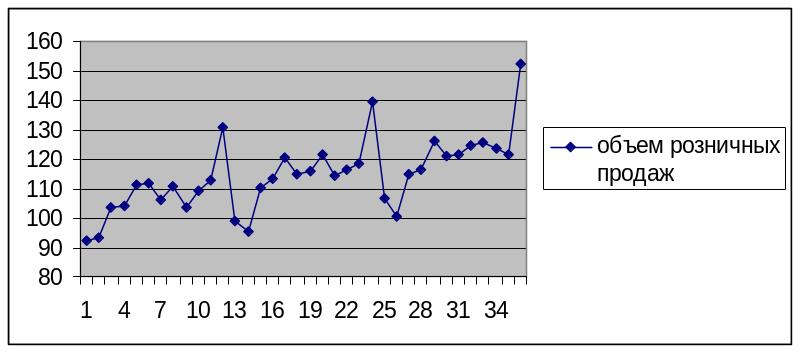
Рис. 2.13

На графике (рис. 2.13) видно, что пик розничных продаж приходится на декабрь месяц. Анализ АКФ и ЧАКФ с учетом сезонной составляющей позволил выбрать модель авторегрессии и проинтегрированного скользящего среднего следующего типа.

Модель ARIMA(p,d,q)(ps,ds,qs) – (1,0,1)(2,1,0) с сезонной задержкой . Выбранную модель можно представить следующим образом:

.

Оценки параметров таковы: ; ; ; , а прогноз представлен графически (рис. 2.14) и расчетными значениями в табл. 2.13.

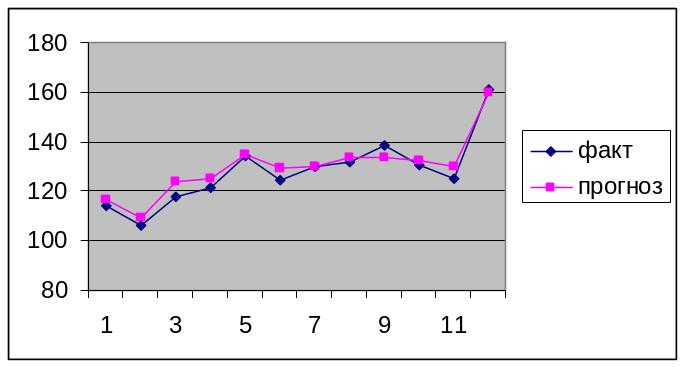
Рис. 2.14

Таблица 2.13

Месяц	Год
	1	2	3	4
				факт	прогноз
1	92,4	98,8	106,7	114,200	116,4
2	93,2	95,6	100,4	106,200	109,4
3	103,8	110,2	114,9	118,100	123,6
4	104,1	113,2	116,3	121,200	125,1
5	111,2	120,5	126,1	134,000	134,7
6	111,7	115,1	121,0	124,600	129,6
7	106,3	115,8	121,4	130,200	130,0
8	110,6	121,4	124,7	132,000	133,4
9	103,4	114,5	125,4	138,700	133,6
10	109,0	116,5	123,8	130,600	132,3
11	112,7	118,7	121,4	125,400	130,2
12	130,9	139,3	152,1	161,200	160,1

Вопросы, задания и ответы

1. В каких случаях можно использовать для прогноза метод среднего абсолютного прироста и метод среднего темпа роста?

2. Выведите систему нормальных линейных уравнений для линейной функции .

3. Запишите в матричном виде для гиперболической функции определение неизвестных коэффициентов и .

4. Используя заданную функцию , вычислите точечный прогноз для периода . Определите доверительный интервал для точечного прогноза, при со стандартной ошибкой прогноза и .

Ответ: ; интервал 12,4-19,6.

5. Определите центрированную скользящую среднюю по следующим квартальным данным 180; 250; 340; 290; 240; 300; 360; 340; 380; 400; 450; 360; 390; 410; 480; 460. Почему для этих данных необходимо центрирование?

Ответ: 272,5; 286,2; 295,0; 303,8; 327,5; 357,5; 381,2; 395,0; 398,8; 401,2; 406,2; 422,5.

6. Имеется ряд динамики 460; 471; 527; 580; 551; 523; 333; 394; 330. Определите выборочный коэффициент автокорреляции при задержке .

Ответ: .

7. Представьте модель ARMA (0,1,2) в общем виде и преобразуйте к разностному виду.

8. По полученой модели AR(2,0,0) вычислите ретроспективный и перспективный прогноз с упреждением , имея следующие данные: 23,7; 23,4; 23,1; 22,9; 22,8; 22,7; 22,5; 22,4.

Ответ: а) ретроспективный прогноз: ; ; ; ; ; ; б) перспективный прогноз: ; .

9. По полученой модели ARIMA(2,0,1) вычислите ретроспективный и перспективный прогноз с упреждением , имея следующие данные: 24; 23,5; 23; 23; 22,8; 22,6; 22,5; 22,4.

Ответ: а) ретроспективный прогноз: ; ; ; ; ; ; б) перспективный прогноз: .