
- •Н.И. Смоглюков Математические методы прогнозирования
- •Содержание
- •Введение
- •Раздел 1. Методы прогнозирования и их классификация
- •1.1. Определение прогноза и его предпосылки. Длительность периода прогноза. Виды прогнозов
- •1.2. Краткая характеристика методов прогнозирования
- •Раздел 2. Прогнозирование одномерных временных рядов
- •2.1. Метод среднего абсолютного прироста
- •2.2. Метод среднего темпа роста
- •2.3. Метод линейного тренда (метод наименьших квадратов)
- •Стандартная ошибка прогноза зависит не только от числа наблюдений n, но и от периода упреждения и определяется по формуле
- •2.4. Модели сезонной декомпозиции
- •2.5. Адаптивные методы прогнозирования
- •Нестационарные модели.
- •Раздел 3. Эконометрические модели прогнозирования
- •3.1. Однофакторные модели прогнозирования
- •3.2. Многофакторные модели прогнозирования
- •3.3. Модель, содержащая несколько уравнений
- •Раздел 4. Динамические модели прогнозирования
- •4.1. Принципы построения непрерывных динамических моделей
- •4.2. Принципы построения конечно-разностных динамических моделей
- •Литература
- •Математические методы прогнозирования
Раздел 2. Прогнозирование одномерных временных рядов
Временной ряд – это последовательность наблюдаемых данных через равные промежутки времени. Чтобы предсказать поведение временного ряда в будущем, необходимо построить модель, и если модель идентифицирована (т.е. подобрана определенного класса модель), то с ее помощью можно осуществить прогноз. Для построения модели необходимо произвести анализ временного ряда. Анализ временного ряда предполагает, что данные содержат несколько компонент: тренд, сезонную, циклическую и случайную ошибку. Большинство методов исследования временных рядов включает различные способы удаления случайной ошибки, чтобы выделить регулярную составляющую.
Тренд представляет собой общую систематическую линейную или нелинейную компоненту, которая плавно изменяется во времени и зависит от влияния долговременных факторов.
Сезонная составляющая – это периодически повторяющаяся компонента во времени, она служит источником краткосрочных колебаний временного ряда.
Циклическая компонента описывает длительные периоды подъемов и спадов. В экономических временных рядах это связано с тем, что экономическая активность не постоянна и имеет периоды подъемов и спадов.
Если временные ряды содержат значительную ошибку, то первым шагом выделения тренда является сглаживание.
Самый
общий метод сглаживания – это метод
скользящего среднего,
в котором каждый член ряда заменяется
средним из n
соседних членов, где
![]() – ширина уровня временного ряда (для
квартальных данных
– ширина уровня временного ряда (для
квартальных данных
![]() ,
а для месячных уровней
,
а для месячных уровней
![]() ).
).
2.1. Метод среднего абсолютного прироста
Средний абсолютный прирост является обобщающим показателем скорости изменения ряда динамики во времени и дает возможность определить, насколько в среднем за единицу времени должен увеличиться (снизиться) уровень ряда в абсолютном выражении, чтобы от начального уровня за данное число периодов достигнуть конечного уровня. Для его определения используют формулу средней арифметической простой
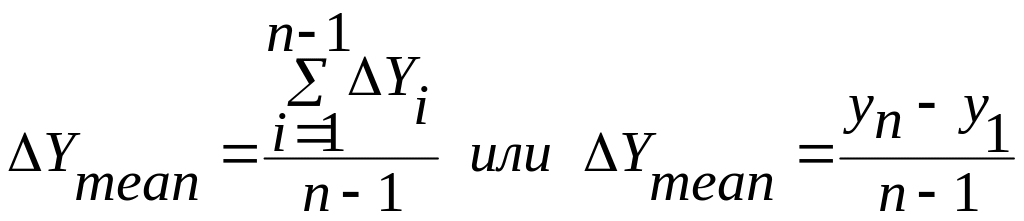 ,
,
где
![]() ;
;
![]() ;
;
![]() – средний абсолютный прирост.
– средний абсолютный прирост.
Прогноз
по данному методу может быть осуществлен
в том случае, если общая тенденция
развития ряда динамики является линейной
либо выполняется следующее условие:
![]() ,
где
,
где
![]() – остаточная дисперсия, которая
определяется по формуле
– остаточная дисперсия, которая
определяется по формуле
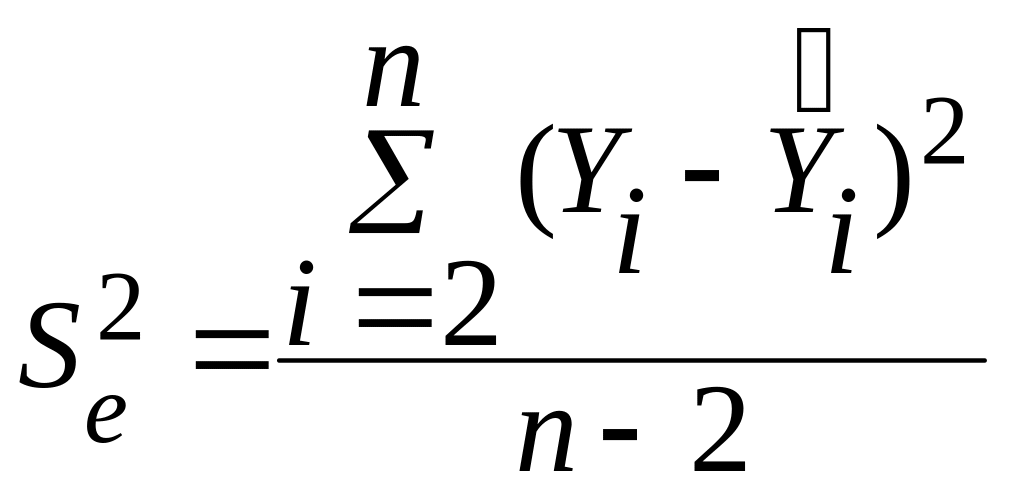 ,
тогда
,
тогда
![]() ;
;
![]() ,
,
где
![]() – теоретическое значение ряда динамики.
– теоретическое значение ряда динамики.
Зная
уровень ряда динамики
![]() ,
принятый за базу экстраполяции, можно
записать экстраполяционную формулу
для прогнозирования ряда динамики
,
принятый за базу экстраполяции, можно
записать экстраполяционную формулу
для прогнозирования ряда динамики
![]() ,
,
где
![]() – период упреждения (
– период упреждения (![]() ).
).
Данный метод позволяет путем последовательного прибавления среднего абсолютного прироста к первому фактическому уровню ряда динамики найти последующие уровни ряда.
Пример 2.1. Имеются следующие данные по объему реализованной продукции по кварталам (табл. 2.1).
Таблица 2.1
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
итого |
|
21,0 |
21,7 |
22,8 |
23,4 |
23,9 |
25,5 |
26,6 |
28,0 |
|
|
– |
0,7 |
1,1 |
0,6 |
0,5 |
1,6 |
1,1 |
1,4 |
7,0 |
|
– |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
|
|
|
0,09 |
0,04 |
0,36 |
1,21 |
0,25 |
0,16 |
0 |
2,11 |
Определим средний абсолютный прирост
![]() или
или
![]() .
.
Определяем теоретические уровни ряда:
![]() и
т.д.
и
т.д.
Определяем
![]() :
:
![]() ;
;
![]() .
.
Так как
условие неравенства выполняется, то
осуществим прогноз на один шаг вперед:
![]() .
.
На графике (рис. 2.1) представлены наблюдаемые и теоретические данные.
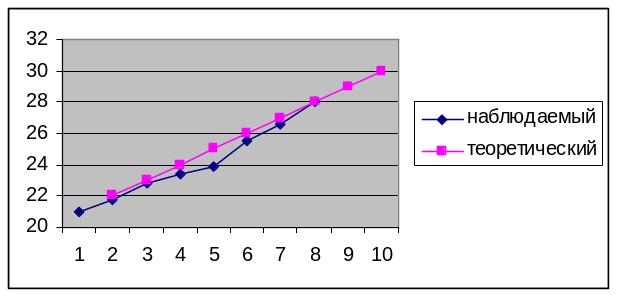
Рис. 2.1
