7.1. Расчет прочности по наклонным сечениям.

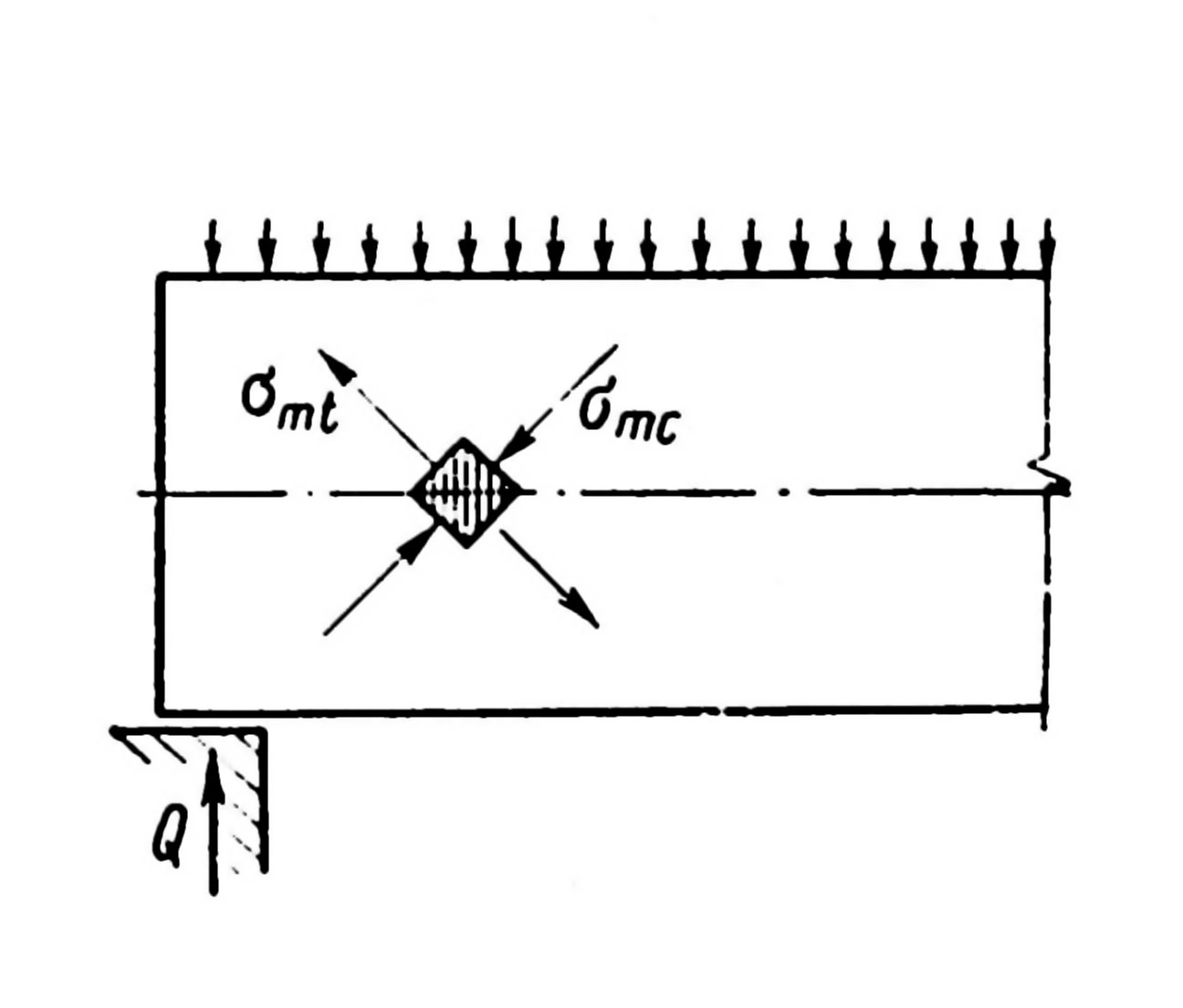
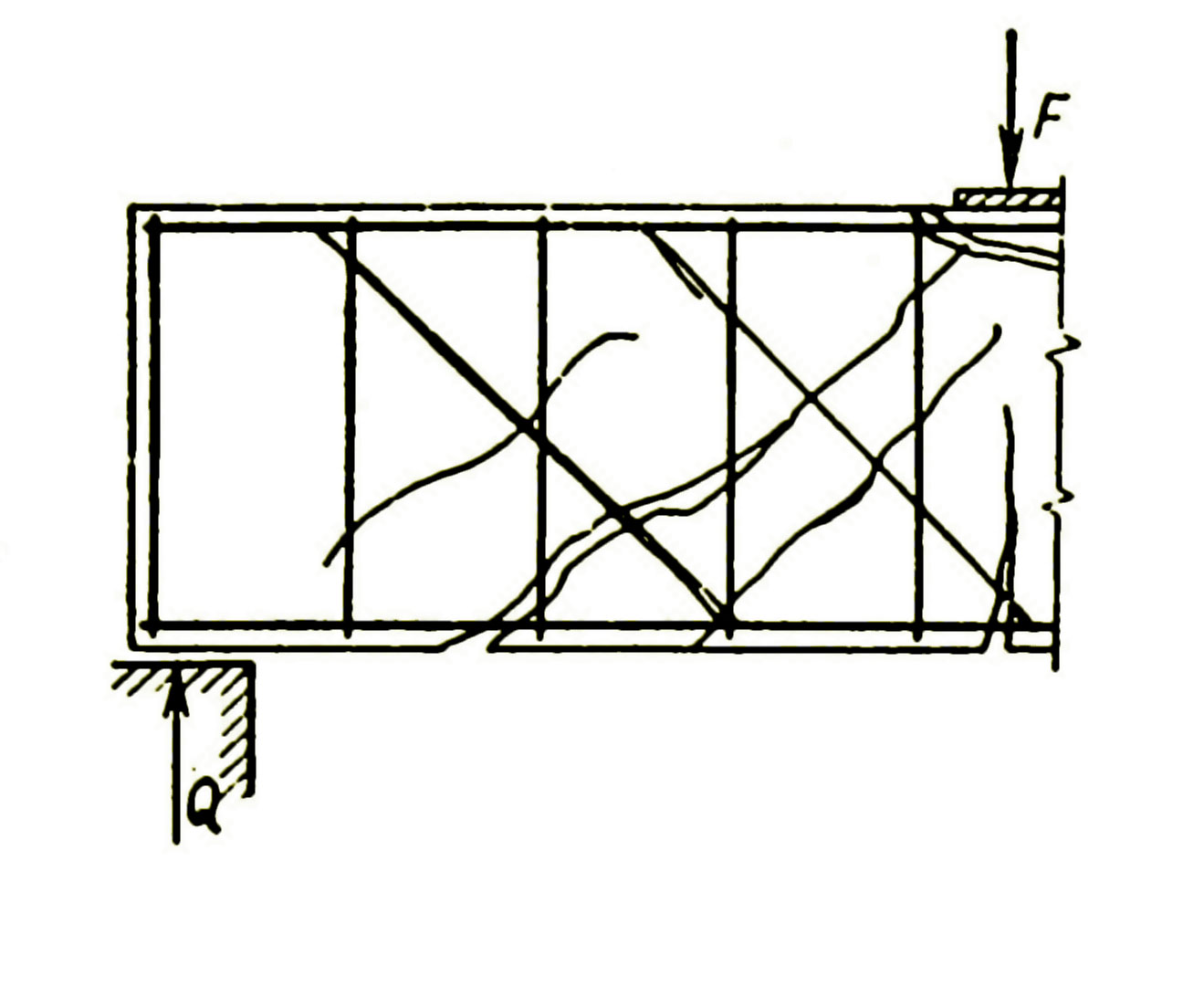
На приопорных участках изгибаемых элементов под воздействием Q и M в сечениях, наклонных к оси, развивается напряженно-деформированное состояние, характеризующееся теми же тремя стадиями, что и в сечениях, нормальных к продольной оси. Главные растягивающие и главные сжимающие напряжения, возникающие под влиянием нормальных и касательных напряжений, действуют под углом к оси (рис. 7.1). Если главные растягивающие напряжения _mt превысят сопротивление бетона растяжению R_bt, возникают наклонные трещины, усилия передаются на арматуру – продольную, поперечную и, в общем случае, отогнутую. При увеличении нагрузки трещины раскрываются, и в конечной стадии происходит разрушение элемента вследствие раздробления бетона над вершиной наклонной трещины и развития напряжений в поперечных стержнях-хомутах до предельных значений; напряжения в продольной арматуре могут и не достигать предельных значений (рис. 7.2).

Рис. 7.1. Главные напряжения в бетоне у опоры балки.	Рис. 7.2. Разрушение балки по наклонному сечению.

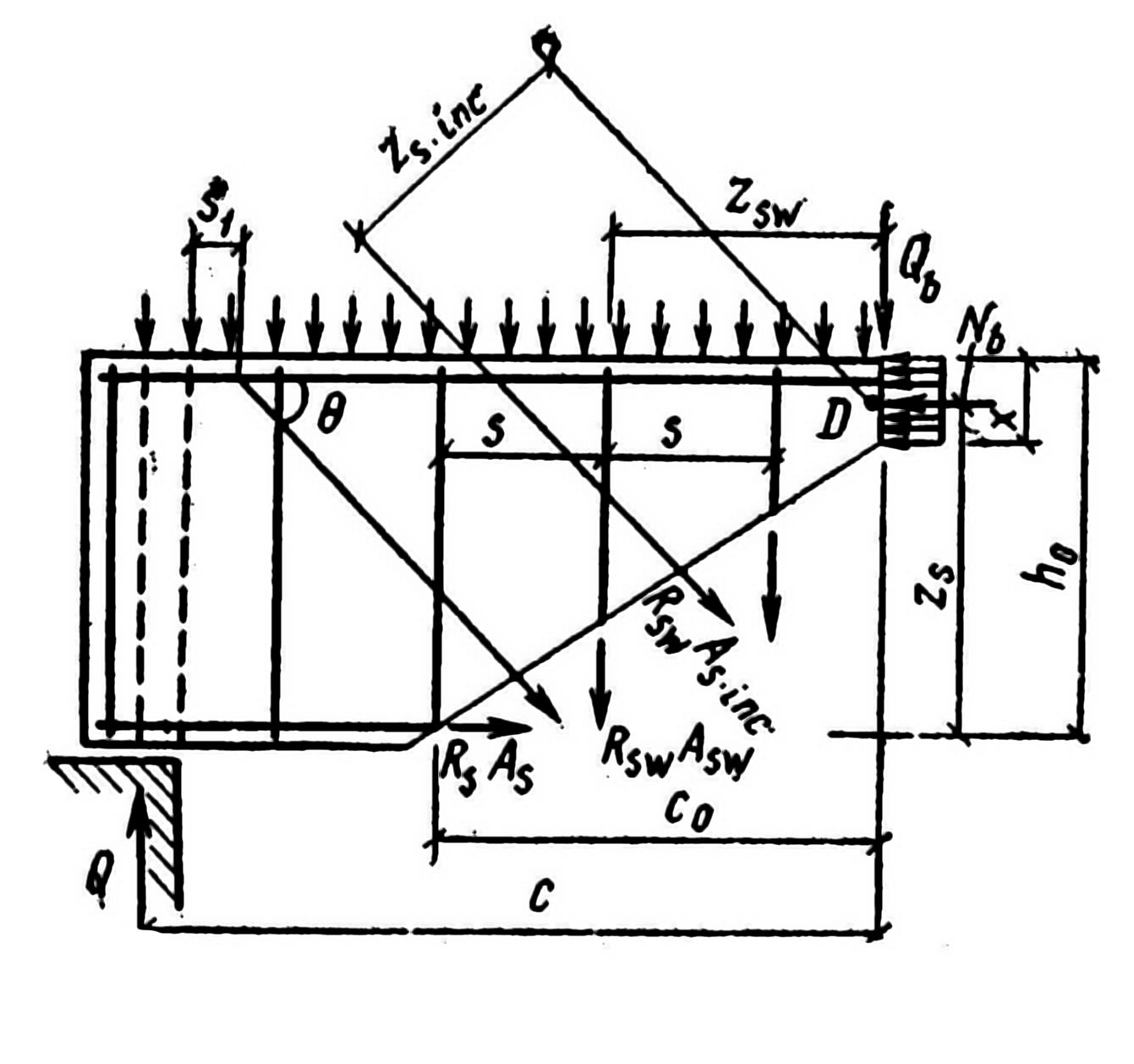
Разрушение изгибаемого элемента по наклонному сечению происходит вследствие одновременного действия на него поперечных сил и изгибающих моментов. Под таким воздействием развиваются внутренние усилия в бетоне сжатой зоны над наклонной трещиной и осевые усилия в арматуре, пересекаемой наклонной трещиной. Расчетная схема усилий в наклонном сечении представлена на рис. 7.3.

	т. D – центр тяжести сжатой зоны сечения; Nb – равнодействующая сжимающих усилий в сжатой зоне сечения; Q – величина поперечной силы на опоре; Qb – поперечная сила, воспринимаемая бетоном сжатой зоны над трещиной; RsAs, RswAsw, RswAs,inc – соответственно равнодействующая напряжений в продольной растянутой, попереч-ной и отогнутой арматуре; S – шаг хомутов; S1 – расстояние от внутренней грани опоры до первого отгиба; Со – проекция расчетного наклонного сечения на продольную ось; С – расстояние от вершины расчетного наклонного сечения до опоры.
Рис. 7.3. Расчетная схема усилий в наклонном сечении.

На рассматриваемом участке внешние воздействия в виде поперечной силы и изгибающего момента уравновешиваются внутренними усилиями в бетоне над вершиной наклонного сечения, а также в продольной и поперечной арматуре.

Расчет прочности выполняют по двум условиям: на действие поперечной силы и на действие изгибающего момента.

Прочность элемента по наклонному сечению на действие поперечной силы обеспечивается условием:

Q  Qb + Qsw + Qs,inc.

(7.1)

В условии (7.1):

(7.2)

и принимается не менее ;

_b2, _b3 – коэффициенты, принимаемые по табл. 7.1 в зависимости от вида бетона;

_f  –  коэффициент, учитывающий влияние сжатых полок в тавровых и двутавровых элементах:

,	(7.3)
где принимается не более . Значение f окончательно принимается не более 0,5;

_n  –  коэффициент, учитывающий влияние продольных сил:

- – при действии продольных сжимающих сил;

- – при действии продольных растягивающих сил.

в формуле (7.2) принимается не более 1,5;

(7.4)

q_sw  –  интенсивность поперечного армирования или величина поперечной силы, воспринимаемая поперечными стержнями на единицу длины элемента:

;

(7.5)

А_sw  –  площадь сечения хомутов в одной плоскости;

.

(7.6)

Таблица 7.1.