Лекция №6. Изгибаемые элементы: два типа задач при расчете изгибаемых элементов прямоугольного сечения с двойной арматурой; расчет прочности по нормальным сечениям элементов таврового профиля.

6.1. Элементы прямоугольного профиля с двойной арматурой.

Rb Rb Ab M Rs As  As  Ab b Rsc As  As

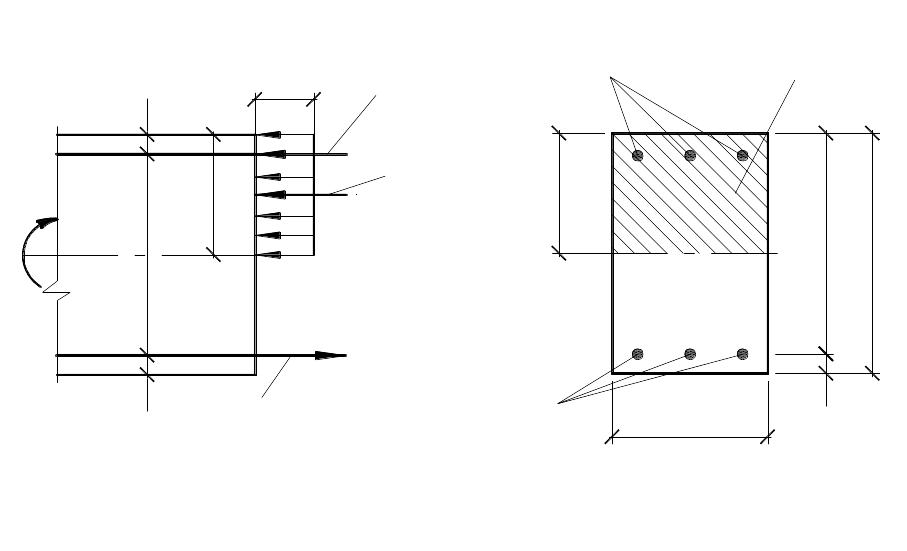
Рис. 6.1. Схема усилий при расчете прочности элемента прямоугольного профиля с двойной арматурой по нормальному сечению.

Если при одиночном армировании изгибаемого элемента прямоугольного сечения оказывается, что   _R, то арматура в сжатой зоне требуется по расчету (рис. 6.1).

Условие прочности изгибаемого элемента прямоугольного сечения, армированного двойной арматурой без предварительного напряжения:

(6.1)

Высоту сжатой зоны х находят из условия (5.19):

(6.2)

При подборе сечений с двойной арматурой по заданных значениях момента М, размеров поперечного сечения bh, класса бетона и класса арматуры возможны задачи двух типов.

Задача 1.  Требуется определить площади сечения растянутой A_s и сжатой A_s арматуры.

Решение.

1) Так как минимальное значение площади сечения сжатой арматуры будет при условии  = _R, то сначала определяем значение граничной относительной высоты сжатой зоны бетона _R по формуле (4.11).

2) Определяем значение коэффициента _m, соответствующее значению _R, из таблиц, приведенных в учебной литературе, либо решив уравнение (5.12).

3) Учитывая выражение (5.12), при х = _Rh₀, требуемою площадь сечения сжатой арматуры находим из условия (6.1):

(6.3)

4) Требуемою площадь сечения растянутой арматуры находим, преобразовав выражение (6.2):

(6.4)

Задача 2.  Задана площадь сечения сжатой арматуры A_s. Требуется определить площадь сечения растянутой арматуры A_s.

Решение.

1) Из условия (6.1), учитывая выражение (5.12), находим

(6.5)

2) Выписываем значение  в зависимости от _m из таблиц, приведенных в учебной литературе, либо решив уравнение (5.14).

3) Определяем значение граничной относительной высоты сжатой зоны бетона _R по формуле (4.11).

4) При условии   _R требуемою площадь сечения растянутой арматуры находим из выражения (6.3):

(6.6)

при значении   _R заданного количества арматуры по площади сечения A_s недостаточно.

6.2. Элементы таврового профиля.

Тавровое сечение образуется из полки и ребра (рис. 6.2) и является выгоднее прямоугольного, поскольку при одной и той же несущей способности (несущая способность железобетонного элемента не зависит от площади сечения бетона растянутой зоны) расходуется меньше бетона вследствие сокращения размеров растянутой зоны. Элементы таврового профиля, как правило, имеют одиночное армирование.

bf1 а) в)

bf b bf1 bf1 c c  As  As 3 2 2 3 1 б) г)

Рис. 6.2. Тавровые сечения (а – балка с полкой в сжатой зоне; б – то же, в растянутой зоне; в – тавровое сечение в составе монолитного перекрытия; г – то же, в составе сборного перекрытия): 1 – полка; 2 – сжатая зона; 3 – ребро.

При большой ширине полок участки свесов, более удаленные от ребра, напряжены меньше. Поэтому в расчет вводят эквивалентную ширину свесов полки b_f1 (рис. 6.2 в, г). Она принимается из условия:

Для отдельных балок таврового профиля (при консольных свесах полок):

свесы полки в расчете не учитывают.

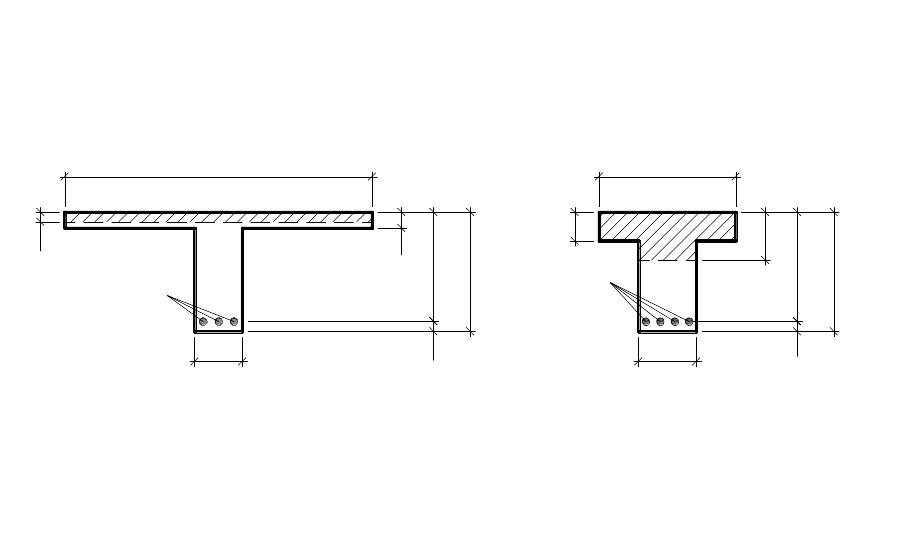
При расчете тавровых сечений различают два случая положения нижней границы сжатой зоны (нейтральной оси): в пределах полки (случай 1) и ниже ее (случай 2) (рис. 6.3).

а) б)
bf b  As bf b  As
Рис. 6.3. Два расчетных случая тавровых сечений: расположение границы сжатой зоны в пределах полки (а) и ниже полки (б).

Если известны геометрические характеристики сечения, внешний изгибающий момент М, класс бетона, класс и количество арматуры, то положение нейтральной оси определяется из условия равенства нулю суммы проекций всех нормальных усилий на продольную ось элемента:

RsAs  Rbbf'hf',

(6.7)

если не известно количество арматуры, то из условия равенства моментов всех сил относительно оси, проходящей через центр тяжести растянутой арматуры:

.

(6.8)

При этом, если условия (6.7), (6.8) выполняются, то нижняя граница сжатой зоны расположена в полке, если не выполняются – в ребре.

При случае 1 тавровое сечение рассчитывается как прямоугольное с размерами b_f'  h₀, поскольку площадь бетона в растянутой зоне на несущую способность не влияет.

Случай 2. В основу положена III стадия НДС. Предпосылки расчета:

1. эпюра напряжений бетона сжатой зоны принята прямоугольной;

2. напряжения в бетоне сжатой зоны и растянутой арматуре достигают предельных значений;

3. бетон растянутой зоны не влияет на несущую способность, и напряжения в нем в сечении с трещиной равны нулю.

Задача расчета состоит в недопустимости достижения конструкцией первой группы предельных состояний, т.е., запроектировать конструкцию так, чтобы усилия в сечении от внешних нагрузок не превышали усилий, которые способна воспринимать конструкция перед разрушением.

Условие прочности получим, приравняв к нулю сумму моментов всех сил относительно оси, проходящей через центр тяжести растянутой арматуры:

.

(6.9)

Высоту сжатой зоны х находят из условия равенства нулю суммы проекций всех нормальных усилий на продольную ось элемента:

.

(6.10)

При х = h₀ и выражения (6.9) и (6.10) приводятся к следующим видам:

,	(6.11)
.	(6.12)

Задача. При заданных значениях изгибающего момента М, класса бетона, класса арматуры, геометрических характеристиках сечения требуется определить площадь сечения растянутой арматуры A_s.

Решение.

1) Из уравнения (6.11) находим

.

(6.13)

2) Выписываем значение  в зависимости от _m из таблиц, приведенных в учебной литературе, либо решив уравнение (5.14).

3) Определяем значение граничной относительной высоты сжатой зоны бетона _R по формуле (4.8).

4) Проверяем условие (5.3), которое может быть представлено в виде:

  R.

(6.14)

5) Определяем значение A_s из выражения (6.12):

.

(6.15)

ЛЕКЦИЯ №7. Изгибаемые элементы: расчет прочности по наклонным сечениям; условие прочности по наклонным сечениям на действие изгибающего момента. Сжатые элементы: конструктивные особенности, расчет условно центрально-сжатых элементов.
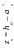
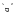
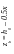
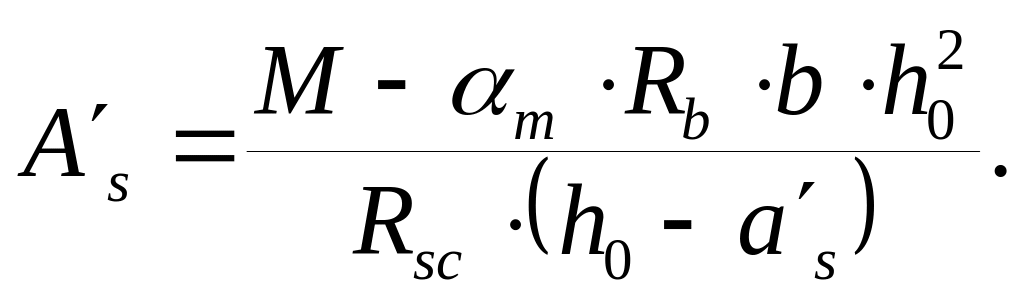
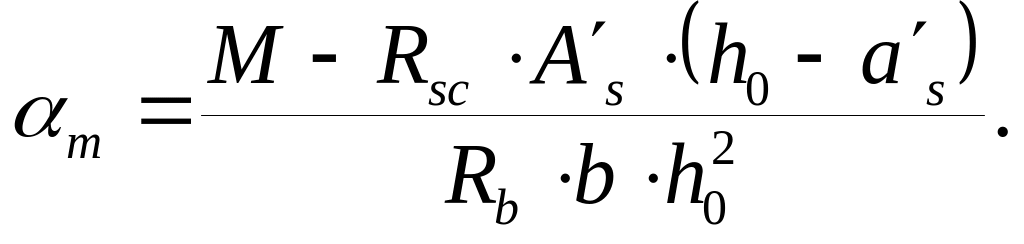
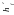
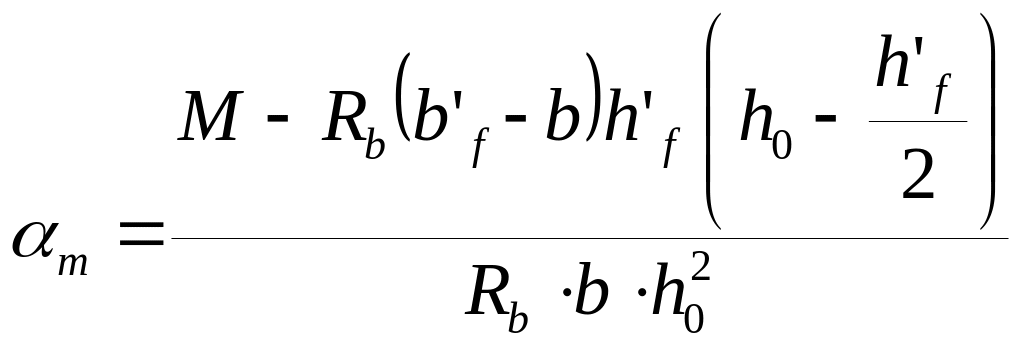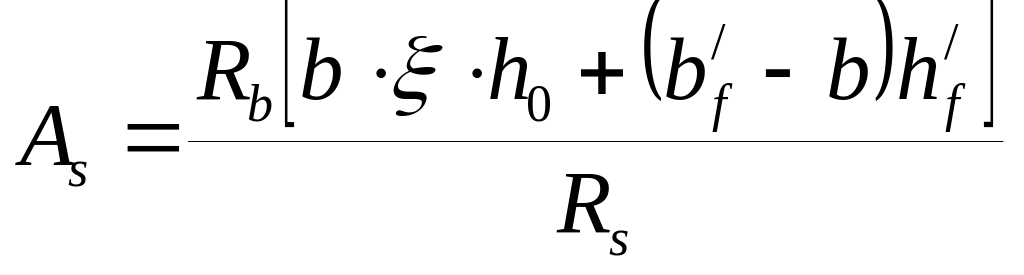