1. 1 Неперервність функції багатьох змінних

Озн. Нехай ф-ція z=f(M) визначена на множині D і точка М₀ є D. Ця ф-ція наз.неперервною у точці М₀ якщо (1) Якщо у точці М­₀ рівність (1) не виконується, т. М0 називаэться точкою розриву ф-ції f(M) , а сама ф-я називаэться розривного у цій точці.

Z =

Lim £ -> 1 y -> 2 (5x – 2y) = 1 ≠ =f(1,2)

Точка М₀(1:2) є точкою розриву ф-ї . Позначемо через (дельта) x = x - x_0,

(дельта)y = y – y₀ , (дельта) z = f(x,y) – f(x₀; y₀)

Озн. Величини х і 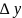наз. Приростами аргументів ф-ї у точці М₀ , а делегину 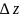наз. Повним приростом ф-ї у цій точці.

Розглянемо (1) :

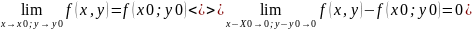
(2)

Із формули (2) випливає іше одне еквівалентне оз-ня неперервності ф-ї багатьох змінних у точці.

Озн. Нехай ф-я z = f(M) визначена на множині D і точка М₀ є D ф-я z=f(M) наз. Неперервною у точці М₀ якщо нескінчено малим прирістом аргументів ф-ї в цій точці і відповідає нескінчено малий приріст

Показати що ф-я z = x­_­­­­­² + y² непереврна на всій області визначення. М₀ (х_0­, у₀ ) – довільна точка є R² : розглянемо М ( х₀ + ; у₀ + )

= f(M) – f(M₀) = (x₀ + ² + (y₀ + 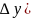² –(x₀² + y₀²) = 2x * + ² +2y0 + ²

Lim = 0 y < означає що ф-я z=х² + у² непереревна у довільній точці М₀ площини R² за 2-м онач. Неперервності, тоді вона неперервна на всій площині R²

Озн. Множина D що міститься в R² наз. Обмеженою якщо існує круг скінченного радіусу що містить в собі цілком площину D

Озн. Множина D наз. Зв’язною якщо будь які її 2 точки можна сполучати неперервною кривою, яка цілком буде ислемати множині D

Трикутник – зв’язна множина 2 трикутники, які не мають скільих внутрішніх точок не є зв’язною

Озн. Точка М₀ є D наз. Внутрішнього якщо існує такий окіл, який цілком належить D. Якщо кожна точка множини D – внутрішня – множину D називають відкритою.

D = { M(x,y)} , x² + y² <1 – відкрита

Озн. Областю наз. Відкриту зв’язну множину точок М(х,у) , x² + y² < 1 – область

Озн. Точка М₀ наз. Межавою точкою множини D , якщо будь який окіл т. М₀ містить точки, які як належать D так і не належать. Множина всіх межових точок D складає межу цієї множини. X² + y² = 1 є межею множини X² + y² < 1

Область : разом з її межею наз. Замкненою областю X² + y² ≤ 1

Для ф-й багатьох змінних аналогом відрізка є замкнена обмежена область, Сформулюємо для точок ф-й аналоги теорем неперервних ф-й однєї зміної.

Теорема 1. Нехай z = F(M) – неперервна у замкненій обмеженій області D тоді ці ф-я обмежена на D: EC > 0AM є D = > |F(M) |<=C

Теорема 2. Нехай z = F(M) – неперервна у замненій обмеженій області D, тоді зона набуває у цій області квото найменшого і найбільшого значення.

Теорема 3. Нехай z = F(M) – неперервна у замкненій обмеженій області D, M₁ , і

M₂ < D, F(M₁) = A, F(M₂) = B, якщо A≠B і число М міститься між А і В існує М* є : F(M*)=M

Зокрема, якщо f(M₁) < 0, f(M₂) >0, EM*<D : F(M*) = 0

Анаологічно, як і для ф-ї однієї змінної для ф-й багатьох змінних побудова складної ф-ї із неперервних ф-й, а також арифметичні дії над неперервними ф-ями приводять до неперервних ф-й.

2. 2 Ф-я багатьох змінних. Границя ф-ї багатьох змінних.

Озн. Нехай D множина упорядкованих пар чисел (х,у), якщо колиному ел-ту (х,у) що належать D міститься R² за деяким правилом або законом відповідає єдине дійсне число Z то кажуть, що на множині D задана ф-я двох змінних z = f(x,y)

V = S/t Швидкість матеріальної точки можна розглядати як ф-ю двох змінних. V = f(S,t)

Озн. Графіком ф-я z = f(x,y) наз. Геометричне місце точок Р(x,y; f(x,y)) Ці точки утворюють у просторі R³ певну поверхню, проекцією якиї на площину xOy є множина D.

Аналогічно можна розглянути оз-ня ф-ї n-змінних

Оз-ня. Нехай множина D складається із упорядкованих наборів п-дійсних чисел (х1, … , хn) , які наз. Точками. Якщо в кожній точці (х1, … , хn) є D < Rⁿ за деяким правилом або законом відповідає єдине дійсне число и, то кажуть, що на множині D задана ф-я U=f(x1,….xn)

Ми будемо розглядати лише ф-ї двух змінних оскільки їх властивості узагальнюються на випадок більшого числа змінних.

Озн-ня. Нехай точка М₀ (х₀; у₀) є R² , б-окылом точки М₀ (б > 0) наз. Множину всіх точок М(х,у) є R² такі що p(M₀, M) = < б

Геометрично б-окіл точки М₀ складається із внутрішніх точок кола із центром у точці М0 радіусом б.

Оз-ня. Нехай задана послідовність точок М1(х1:у1), М2(х2:у2) … Мn(xn, yn) яку будемо позначати {Mn}n=1 до безконечності Точка М0 (х0;у0) наз. Границею цієї послідовності якщо для будь якого б>0 існує номер N що залежить від б, такий що для всіх членів послідовності {Mn} n=1 до безконечности з номерами n > N виконується нерівність з (М0, Мn) < б. Границю називаються lim n->∞ ( Mn = M₀) або Mn - > M₀ n -> ∞

Оз-ня. Нехай ф-я z = f(x,y) визначена на множині D, точка М₀ є D або т. М0 не пренадлежи D, але у цьому випадку будь які окіл т. М0 містить точки множини D. Число А наз. Границэю ф-ї z = f(x,y) = f(M) у точці М0 якщо для будь якої послідовності точок {Mn}n=1 де Mn є D, Mn - > M0, n - > ∞ але Mn ≠ M0, Послідовність відповідних значень ф-й {f(M0)} n = 1 до безконечності має границю А. lim n->∞ ( f(Mn)=A) Позначають lim M->M0 ( f(M) = A)

Наведена означення наз. Означенням границі ф-ї у точці на мові послідовностей. Розглянемо еквівалентне оз-ня на мові

Оз-ня. Нехай т. М₀ задоволення попереднім умовам. Число А наз. Границею ф-ї z=f(M) у цій точці, якщо для будь якого E > 0 існує б > 0 яке залежить від Є таке що для всіх точок М є D і задовольняють нерівність 0 < p(M₀; M) < б виконується нерівність |f(M)-A| < E

Для ф-ї двох змінних виконується всі теореми про границі, що були у ф-ї однієї змінної. Зокрема

Теорема 1. Нехай ф-ї z = f(x,y) і z = p(x,y) мають у т. М₀(x₀; y₀) границі А і В відповідно тоді ф-ї f(x,y) ± p(x,y) f(x,y) * p(x,y), мають у т. М0 границі що відповідно дорівнюють А ± В , А*В, А/В(В≠0)

Озн-ня. Ф-я α = α(М) наз. Нескінченно малою у т. М₀, якщо lim M->M0 ( α(M) = 0 )

Теорема 2. Для того, щоб ф-я z = f(M) мала у точці М₀ границю А необхідно і достатньо щоб f(M) = A + α(M), де α(М) – нескінченно мала у точці М₀ функція.