4. Анализ качества системы

4.1. Оценка качества системы по графику переходного процесса

Прямой метод оценки переходного процесса в системе заключается в получении графика переходного процесса и оценки качества системы по нему.

Для построения переходного процесса необходимо определить уравнение переходного процесса. Передаточная функция замкнутой системы имеет вид:

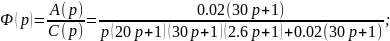(8.0.)

; (8.1.)

Из передаточной функции замкнутой системы (8.1.) записываем дифференциальное уравнение системы в операторной форме:

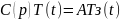(8.2.)

В таком случае дифференциальное уравнение системы в операторной форме примет вид:

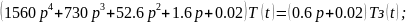(8.3.)

Структурная схема замкнутой системы представлена на рисунке 8

Рис. 10. Структурная схема замкнутой системы

Для того, чтобы построить график переходного процесса, необходимо решить дифференциальное уравнение численным методом. Для этого разбиваем передаточную функцию на две составляющие, как показано на рисунке 9.

Рис. 11. Преобразованная структурная схема замкнутой системы

В качестве входного воздействия принимается единичная ступенчатая функция .

Сводим решение дифференциального уравнения к решению задачи Коши, путем перехода к фазовым координатам. Для построения графика переходного процесса используем систему MathCAD-14.

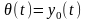
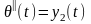
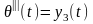
Подставляя значения фазовых координат в (8.3.), получаем

(8.4.)

Преобразуем первое уравнение системы уравнений (8.4.) в следующий вид:

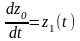
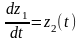
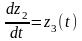
Общее решение уравнений найдем по формуле:

(8.5.)

Решение полученной системы с помощью программы MathCAD-14:

.

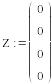
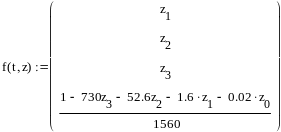
Результаты вычислений приведены в таблицах 5 и 6.

График переходного процесса системы представлен на рис. 10.

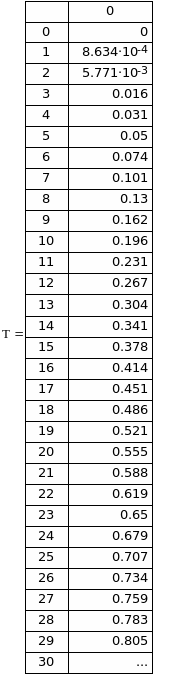
Таблица 5. Изменение значений z(t). Таблица 6. Изменение значений T

Рис. 12. График переходного процесса в системе пленочного абсорбера.

4.2. Оценка качества системы по логарифмическим характеристикам

При оценке качества системы пленочного абсорбера по логарифмическим частотным характеристикам (рисунок 6) необходимо определить характер и длительность процесса в системе, а так же запас устойчивости системы[2].

Характер процесса в системе определяется среднечастотным участком логарифмической амплитудной характеристики (ЛАХ), примыкающим к частоте среза ω_с системы. Плавный апериодический процесс без перерегулирования возможен в системе только при наклоне асимптоты среднечастотного участка ЛАХ в пределах ±0,6 декады от частоты среза ω_с, равном – 20 дБ/дек. Для исследуемой системы данный интервал составляет не менее 0,7 декады от частоты среза w_c.

Длительность переходного процесса определяет быстродействие системы и связана с частотой среза ω_с системы:

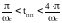, (9.0.)

где ω_с=0.017с^-1 – частота среза системы. Подставив численные значения, получим:

. Данное неравенство определяет верхнюю и нижнюю границу длительности переходного процесса в исследуемой системе. В нашем случае t_пп=120 с. Данное значение полностью удовлетворяет неравенство.

Запас устойчивости характеризует степень устойчивости системы автоматического управления. Различают запас устойчивости системы по фазе и запас устойчивости по амплитуде , где ω_π – частота, соответствующая углу фазового сдвига .

В системах, обладающих достаточным качеством, запас по фазе должен составлять не менее 20˚-50˚. Запас устойчивости системы по амплитуде связан с перерегулированием в системе: с увеличением перерегулирование в системе снижается.

Для рассматриваемой системы данные показатели составляют:

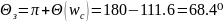
Проанализировав логарифмические частотные характеристики исследуемой системы, можно заключить, что система пленочного абсорбера полностью удовлетворяет всем критериям качества системы.