3. Анализ устойчивости системы

3.1. Оценка устойчивости системы по алгебраическому критерию Гурвица

При исследовании системы с использованием критерия устойчивости Гурвица, рассматривается характеристический полином замкнутой системы. По Гурвицу для устойчивой системы должны соблюдаться два условия:

1-Коэффициенты характеристического полинома должны быть больше нуля.

2-Должны быть положительны определители, составленные из этих коэффициентов.

Характеристический полином замкнутой исследуемой системы с добавлением регулятора имеет следующий вид

(6.0.)

Произведем проверку по алгебраическому критерию Гурвица:

1. С₀= , С₁=730, С₂=52,6, С₃=1,6, С₄=0,02 >0следовательно первый критерий выполняется.

2. Вычислим определители, составленные из этих коэффициентов.

Для системы четвертого порядка имеем:

Δ₃= С₁ С₂ С₃ - С₄ - С₀ = 46785,2 >0.

Определитель получился положительным, следовательно, критерий устойчивости Гурвица подтверждает устойчивость разработанной системы.

3.2. Построение области устойчивости в плоскости параметров Тд и Кр

Исследование проводится методом D – разбиения, изложенным в [2], область устойчивости строится в плоскости двух задаваемых параметров. Для выполнения исследования необходимо найти характеристический комплекс системы.

Характеристический полином системы имеет вид:

(7.0.)

Видоизменим характеристический полином и представим его в виде:

(7.1.)

Преобразуем характеристический полином к виду, удобному для построения.

=

Преобразуем характеристический полином в характеристический комплекс путем подстановки p=iw.

(7.2)

Д алее находим вещественную X() и мнимую Y() части характеристического комплекса, затем параметрические уравнения границы устойчивости системы (по критерию Михайлова).

X()=0

Y()=0

В нашем случае получаем

X()= =0 (7.2.)

Y()=

П роизведем с системой (7.2.) ряд преобразований:

k=

k = (7.3)

(7.4.)

.

Зададим ряд значений  в приделах и построим график зависимости и .

Так как частота  входит в параметрические выражения границы области устойчивости (3.2.3.) в четной степени, то достаточно рассмотреть только область положительных частот , поскольку при отрицательных значениях частоты, будут получаться те же точки, что и при соответствующих положительных значениях частоты.

По табличным данным производим построение колебательной границы устойчивости.

Определим дополнительные границы области устойчивости, для этого приравняем к нулю первый коэффициент характеристического многочлена (7.2.) и его свободный член:

(7.5.)

.

K=0; (7.6.)

T=0.

Для определения расположения области устойчивости относительно границ воспользуемся правилом штриховки [2], для этого составим определитель вида

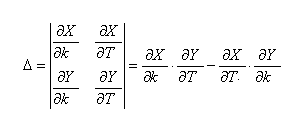
где k(w) и T(w) – исследуемые параметры.

В нашем случае, на основании (7.6.) получаем:

Δ= =

По правилу штриховки, следует, что если >0, граница штрихуется слева при движении по ней в направлении от к , а если <0, то справа в тех же условиях. При соблюдении этого правила штриховка будет направлена внутрь области устойчивости.

В нашем случае ,следовательно  может принимать как положительные, так и отрицательные значения. То есть при отрицательных значениях  <0 ,а при положительных  >0.

Так как  входит в параметрические уравнения (7.4.) в четной степени, штриховка дополнительных границ устойчивости производится по смыслу.

Необходимо произвести проверку построения области устойчивости. Для этого на получившемся графике (см.рис.9 .) отметим контрольную точку М_контр , с координатами и , соответствующими параметрам нашей системы терморегулирования Она попадает в построенную область устойчивости, следовательно, можно в первом приближении полагать, что область устойчивости построена верно.

Рис.9. Область устойчивости