
- •1.3. Потенциалы электромагнитного поля.
- •О роли лоренцевой калибровки в уравнениях электродинамики
- •Случай плоских однородных гармонических волн в вакууме.
- •Общее решение уравнений классической электродинамики.
- •Проводящая однородная изотропная среда в отсутствие сторонних электрических зарядов.
- •Потенциал Герца магнитного типа.
- •Комплексные силовые составляющие и потенциалы электромагнитного поля.
- •Потенциалы Дебая.
Случай плоских однородных гармонических волн в вакууме.
Рассмотрим скалярную однородную плоскую
гармоническую волну с волновым вектором
![]() и круговой частотой
и круговой частотой
![]() ;
;
![]() (75)
(75)
Напомним определение оператора "лапласиан":
![]() (76)
(76)
Последовательно вычислим выражения
![]() (77)
(77)
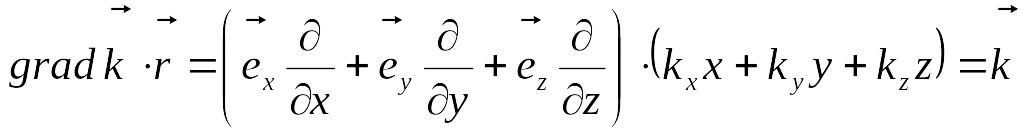 (78)
(78)
![]() (79)
(79)
![]() (80)
(80)
В итоге получаем соотношение:
![]() (81)
(81)
фазовая скорость волны:
![]() (82)
(82)
Воспользуемся полученными результатами для анализа однородной плоской гармонической электромагнитной волны;
![]() (83)
(83)
![]() (84)
(84)
![]() (85)
(85)
![]() (86)
(86)
калибровка Лоренца
![]() (87)
(87)
приводит к уравнению:
![]() (88)
(88)
условия удовлетворения этому требованию:
![]()
![]()
![]() (89)
(89)
Из (88) следует соотношение между амплитудами компонент векторного потенциала и амплитудой скалярного потенциала:
![]() (90)
(90)
В соответствии с определением потенциалов электромагнитного поля получаем зависимости
![]()
![]() (90)
(90)
следствия:
![]() волна поперечная (91)
волна поперечная (91)
действительно:
![]() (92)
(92)
для плоских однородных гармонических волн все свойства доказаны
вектор нормали к волновому фронту
![]() (93)
(93)
вектор Пойнтинга (он не является линейной функцией, требуется переход от комплексных выражений к действительным выражениям)
![]() (94)
(94)
![]() (95)
(95)
![]() (96)
(96)
![]() (97)
(97)
![]() (98)
(98)
![]()
![]() (99)
(99)
С учётом соотношения
![]() (100)
(100)
получаем выражение для мгновенного значения вектора Пойнтинга
![]() (101)
(101)
основной результат при этом состоит в том, что вектор Пойнинга в рассматриваемом случае совпадает по направлению с волновым вектором, который перпендикулярен плоскости волнового фронта:
![]() (102)
(102)
Продолжение
Калибровка Кулона.
Условие калибровки Лоренца не является исчерпывающим: можно ещё наложить добавочное ограничение на потенциалы электромагнитного поля. В частности, можно дополнительно потребовать выполнение условия
![]() (103)
(103)
В этом случае уравнение для скалярного потенциала электромагнитного поля принимает вид уравнения Пуассона
![]() ,
(104)
,
(104)
решение которого для безграничного пространства можно записать в форме интеграла Пуассона:
![]() (105)
(105)
Уравнение для векторного потенциала при этом переходит в неоднородное волновое уравнение с известной правой частью
![]() (106)
(106)
Решение полученного "стандартного" уравнения рассматривается в курсах математической физики.
Поскольку уравнение (103) приводит к уравнению Пуассона (104) и решению в форме интеграла Пуассона (105), уравнение (103) называют калибровкой Кулона (кулоновская калибровка).
