4.2 Применение рекомендаций по выбору средств измерений
Конкретное средство измерения выбирается по таблицам V…IX [5]. В левой части таблиц указаны диапазоны номинальных размеров, сверху квалитеты, а на пересечении горизонтальных строк и вертикальных колонок указаны в виде дроби допускаемые погрешности измерений (числитель) и допуски на изготовление (знаменатель). Под номерами и буквами в таблицах I и II [5] указаны позиции измерительных средств и варианты их использования, при которых предельная погрешность измерений не превышает допускаемых значений, т.е. соблюдается условие (4.1).
Предельные и допускаемые погрешности измерений в таблицах I, II, V – IX указаны без знаков ±(плюс, минус), т.е. указаны абсолютные значения.
4.3 Порядок выполнения работы
4.3.1 Выполнить эскиз заданной детали с указанием номинального размера измеряемой поверхности.
4.3.2 Определить комбинированное обозначение размера пользуясь таблицами ГОСТ [6,7]
4.3.3 Из таблиц V – IХ [5] выписать значение допускаемой погрешности и позиции рекомендуемых средств измерений.
4.3.4 Из таблиц 1 и 2 [5] выбрать конкретное средство измерения (имеющиеся в наличии средства измерений отмечены кружочками).
4.3.5 Измерить указанные на эскизе размеры по девять раз, рассчитать средний размер и показать его на схеме полей допусков.
4.3.6 Полученный средний размер записать с учетом предельных погрешностей средств измерений.
Таблица 4.1 Основные параметры размеров детали
№№ размеров по эскизу |
Условное обозначение размера |
Комбинированное обозначение размеров |
Допускаемая погрешность измерения |
Позиции рекомендуемых средств |
Наименование инструмента и предел измерения |
Предельная погрешность измерения |
Результаты измерения |
Абсолютная погрешность отдельных измерений, X¯-Xi |
Квадраты абсолютных погрешностей (X-Xi)2 |
|
|
|
|
|
|
|
|
|
|
4.3.7 Вычислить абсолютные погрешности отдельных измерений
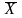ΔXi
=
- Xi
4.3.8 Вычислить квадраты абсолютных погрешностей (ΔXi)2
4.3.9 Вычислить
сумму квадратов абсолютных погрешностей
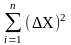
4.3.10 Вычислить среднеквадратическую погрешность результата серии измерений по формуле:
,
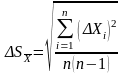(4.2)
где
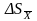- выборочная дисперсия или дисперсия
выборки.
При ограниченном
числе n величина
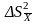является лишь оценкой дисперсии
,
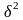а не равна ей.
Среднеквадратическая погрешность характеризует рассеивание средних арифметических, т.к. из-за случайных погрешностей результаты измерений также являются случайными величинами, и если выполнить еще одну серию измерений, то полученное новое среднее арифметическое будет несколько отличаться от ранее найденного значения.
4.3.11 Задать
значение надежности α (таблица 4.2) и
определить коэффициент Стьюдента
.
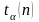4.3.12 Вычислить границы доверительного интервала по формуле:
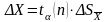(4.3)
4.3.13 Записать разброс значений измеряемого параметра с учетом среднего арифметического значения и доверительного интервала
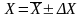или
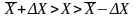
4.3.14 Величина абсолютной погрешности результата измерений сама по себе еще не определяет точность измерений. Для оценки точности измерений вводится понятие относительной погрешности ε. За меру точности измерения принимают величину, обратную ε.
4.3.15 Вычислить относительную погрешность с учетом предельной погрешности средства измерения
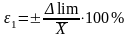
4.3.16 Вычислить относительную погрешность с учетом доверительного интервала
;
4.3.17 Сделать вывод о годности детали и сравнив ε1 с ε2 дать заключение о методах оценки точности.
Таблица 4.2 Коэффициенты Стьюдента, t
α n-1 |
0,9 |
0,95 |
0,98 |
0,99 |
0,999 |
1 2 3 4 5 6 7 8 9 10 11 12 |
6,31 2,92 2.35 2,13 2,02 1,94 1,89 1,86 1,83 1,81 1,80 1,78 |
12,7 4,3 3,18 2,78 2,57 2.45 2,36 2,31 2,26 2,23 2,20 2.18 |
31,8 6,96 4,54 3,75 3,36 3,14 3,00 2,90 2,82 2,76 2.72 2,68 |
63,7 9,92 5,84 4,60 4,03 3,71 3,50 3,36 3,25 3,17 3,11 3,05 |
636,6 31,6 12,9 8,61 6,87 5,96 5,41 5,04 4,78 4,59 4,44 4,32 |