2.9.1. Функция распределения непрерывной случайной величины

Функция распределения случайной величины X определена в разделе 2.3: . Эта функция называется также интегральной функцией распределения.

Если случайная величина X – непрерывная, то функция распределения является непрерывной функцией на всей прямой и удовлетворяет всем свойствам, сформулированным ранее в разделе 2.3, т.е. ; – неубывающая функция; и вероятность попадания случайной величины Х в промежуток равна .

Теорема. Если X – непрерывная случайная величина, то .

Действительно, в силу формулы (2.3), . Устремим , тогда и .

Следствие. Для непрерывной случайной величины X справедливы равенства

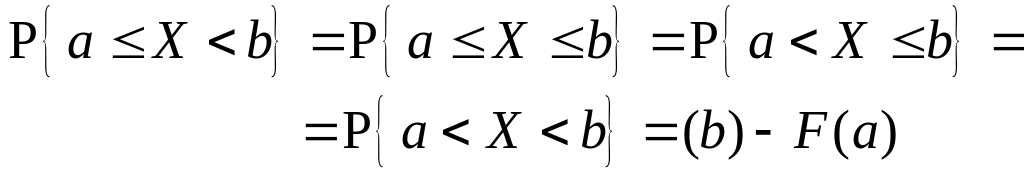(2.29)

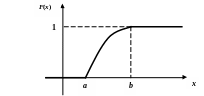
Замечание. Если возможные значения случайной величины X принадлежат отрезку , то из определения (2.9) вытекает, что при , и при . График функции распределения непрерывной случайной величины X в этом случае имеет вид

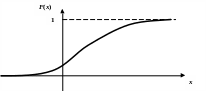
Если возможные значения случайной величины X расположены на всей оси, то и . В этом случае график функции распределения непрерывной случайной величины имеет горизонтальные асимптоты (влево) и (вправо):

2.9.2. Плотность распределения вероятностей

Определение 2.20. Плотностью распределения вероятностей (или плотностью распределения, или плотностью вероятностей) непрерывной случайной величины X называется производная функции распределения:

, . (2.30)

Функцию называют также дифференциальной функцией распределения.

График плотности распределения называется кривой распределения. Из формулы (2.30) вытекает, что функция распределения может быть выражена через плотность по формуле

, . (2.31)

Свойства плотности распределения

1. , .

2. Вероятность того, что непрерывная величина X примет значение, принадлежащее отрезку , равна

. (2.32)

В частности,

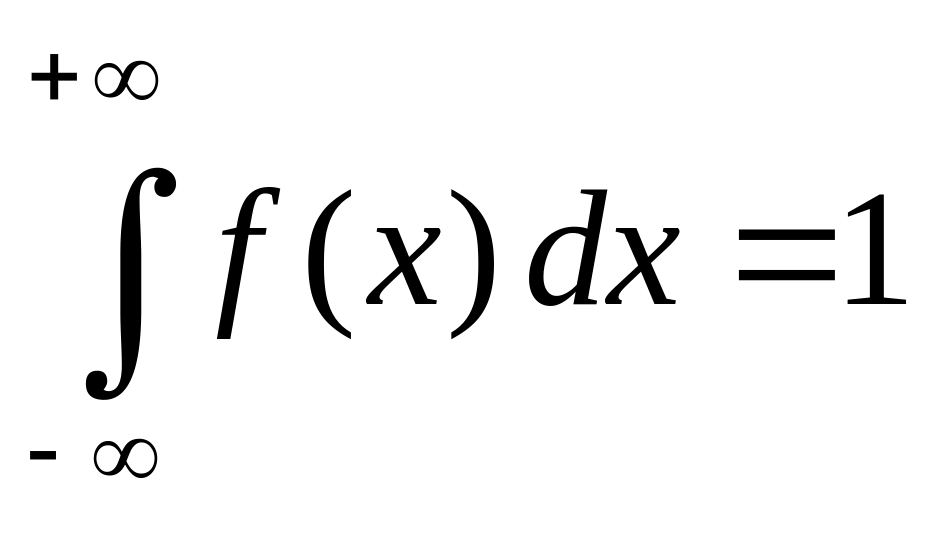. (2.33)

Пример 2.15. Задана функция распределения

.

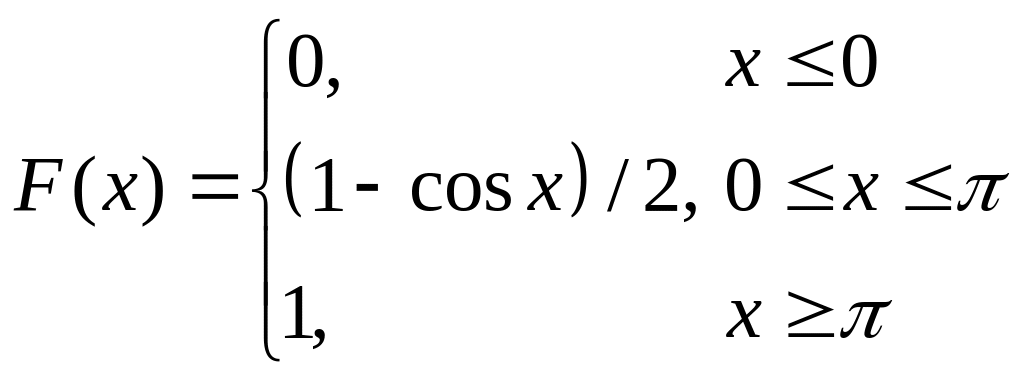Требуется найти плотность распределения , построить графики и ; и вычислить вероятность того, что в результате испытания X примет значение, принадлежащее интервалу .

Решение. В силу формулы (2.30), .

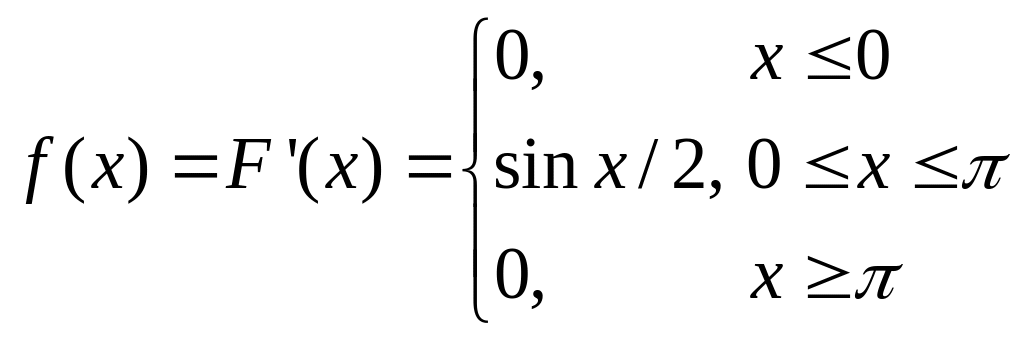Построим графики и :

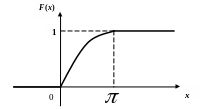
Наконец, вычислим вероятность , используя формулу (2.29):

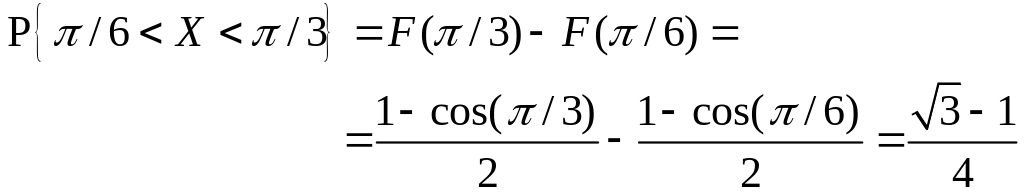
Пример 2.16. Задана плотность распределения .

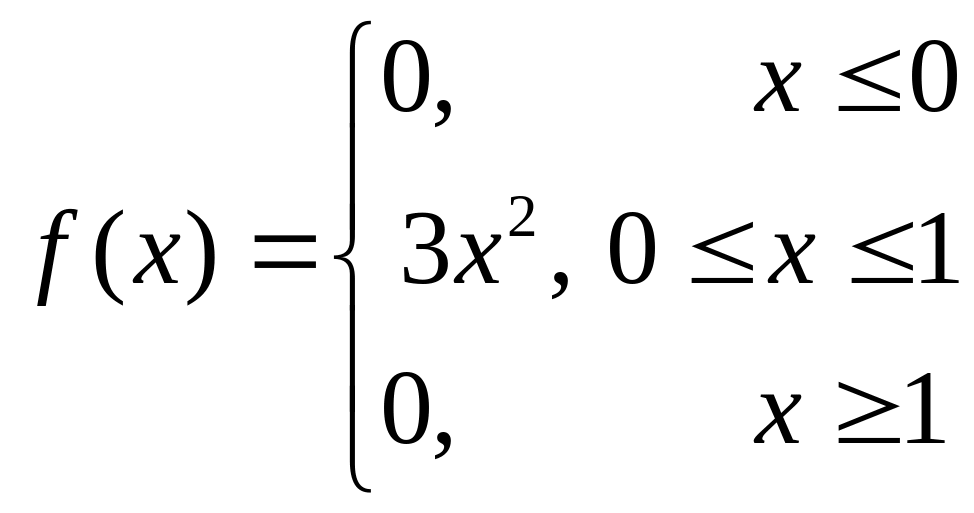Найти функцию распределения .

Решение. Пусть . Тогда в силу формулы (2.31), , так как при . Если , то

.

Если , то

.

Таким образом,

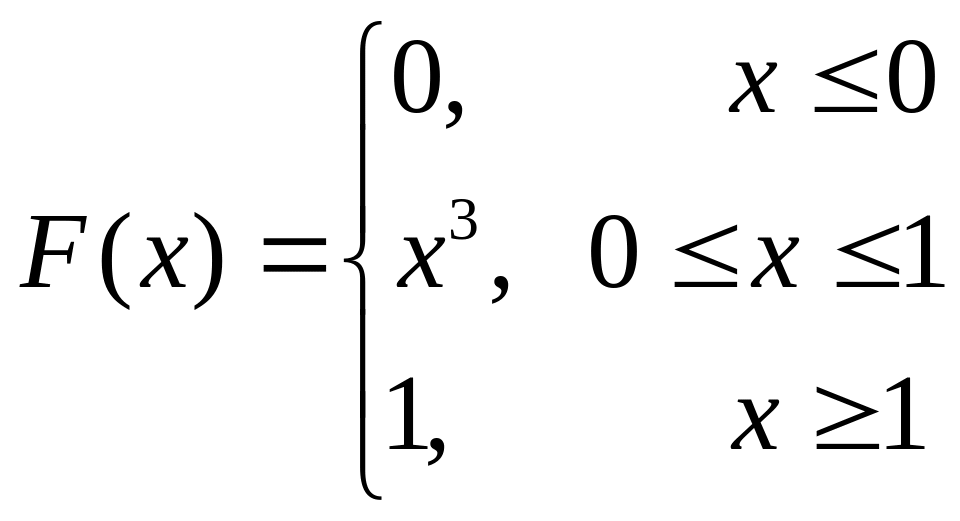
2.9.3. Числовые характеристики непрерывной случайной величины

Числовые характеристики непрерывной случайной величины аналогичны числовым характеристикам дискретной случайной величины (см. раздел 2.7).

1) Математическое ожидание для непрерывной случайной величины равно

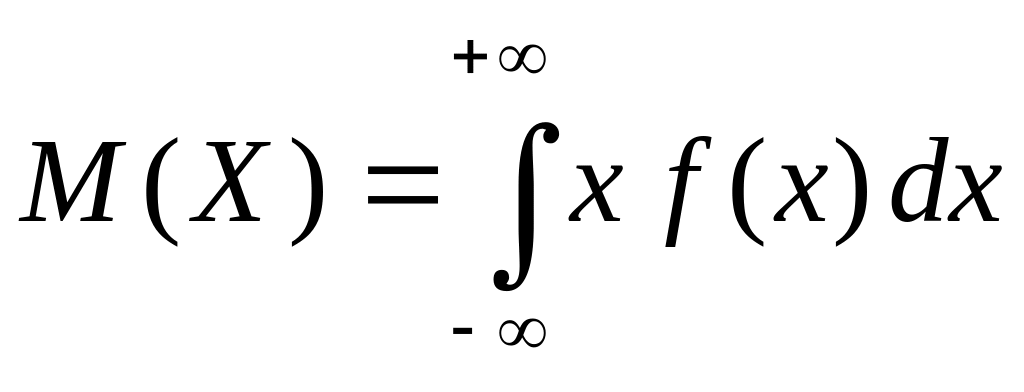(2.34)

(интеграл должен быть абсолютно сходящимся).

2) Дисперсия для непрерывной случайной величины определяется по формуле

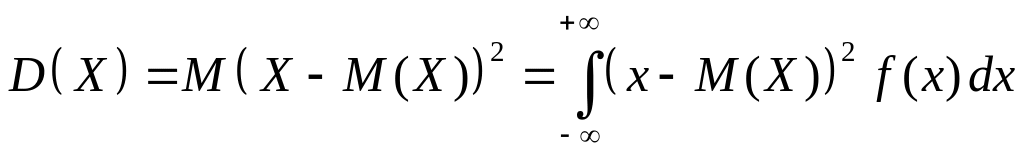. (2.35)

(интеграл должен быть сходящимся, в противном случае говорят, что случайная величина не имеет дисперсии).

Иногда для вычисления дисперсии удобно использовать следующую формулу

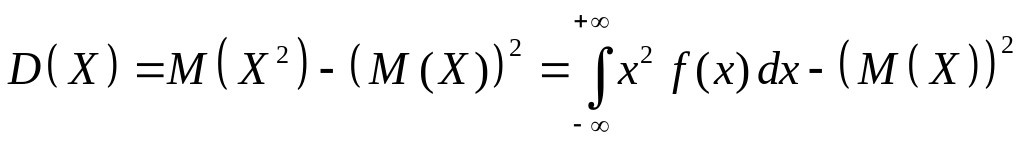. (2.36)

3) Среднее квадратическое отклонение случайной величины X равно

. (2.37)

4) Начальный момент порядка k равен

.

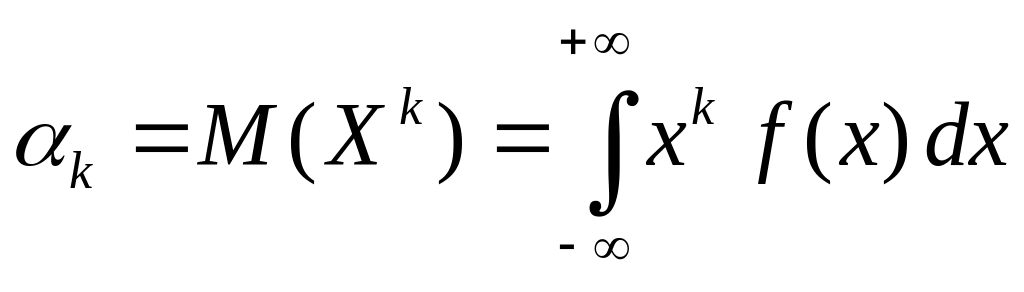5) Центральный момент порядка k равен

.

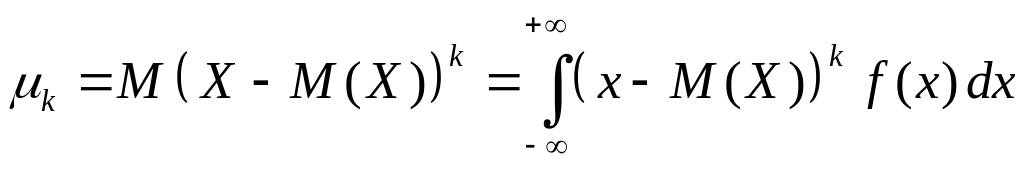6) Модой непрерывной случайной величины X называется такое ее значение , для которого .

7) Медианой случайной величины X называется такое ее значение , для которого выполняется условие или .

Пример 2.17. Задана функция распределения 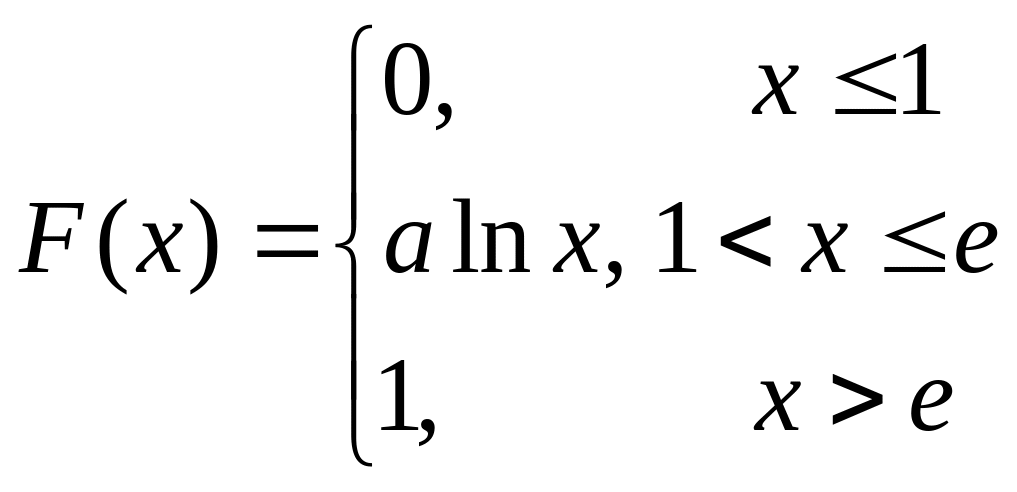. Требуется: а) найти значение a; б) найти плотность распределения ; в) построить графики и ; г) вычислить математическое ожидание, дисперсию и медиану; д) вычислить вероятность того, что X примет значение, принадлежащее интервалу .

Решение. а) Так как функция непрерывна на всей оси, то, в частности, непрерывна при , т.е. . Следовательно, . Поэтому .

б) В силу формулы (2.30),

.

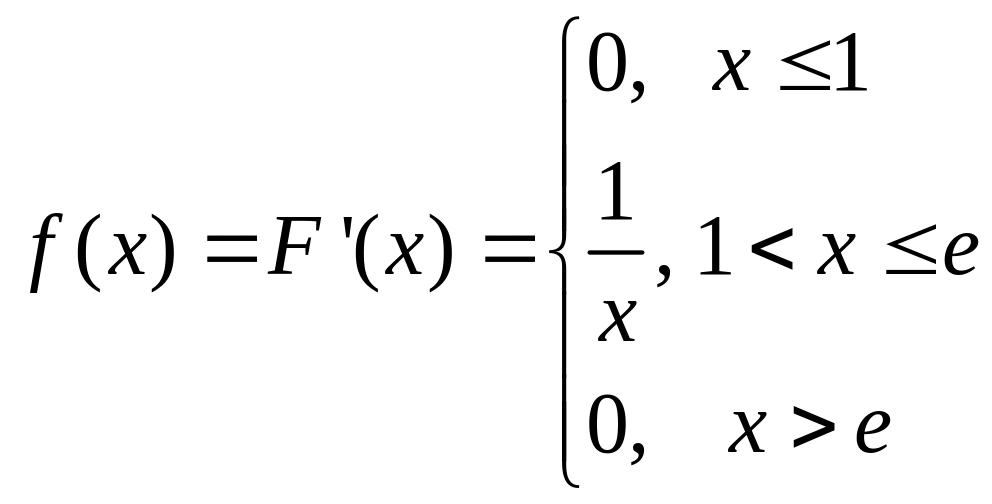в) Построим графики и :

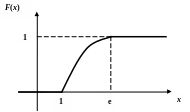
г) Вычислим математическое ожидание, используя формулу (2.34):

.

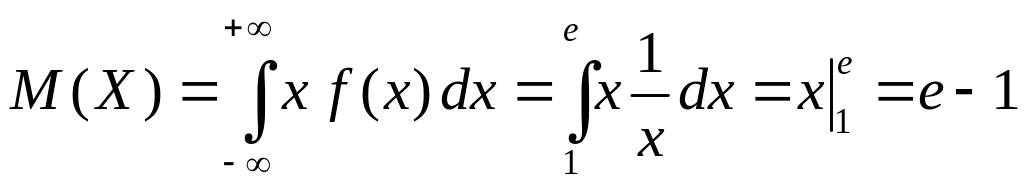Вычислим дисперсию, используя формулу (2.36):

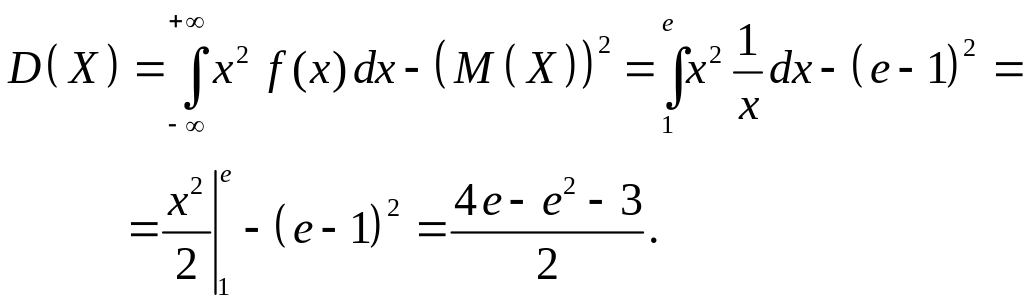
Вычислим медиану , используя равенство . Подставляя в выражение для , получаем . Следовательно, медиана равна .

д) Вычислим вероятность

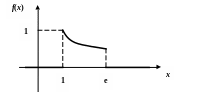
Пример 2.18. Задана плотность распределения

.

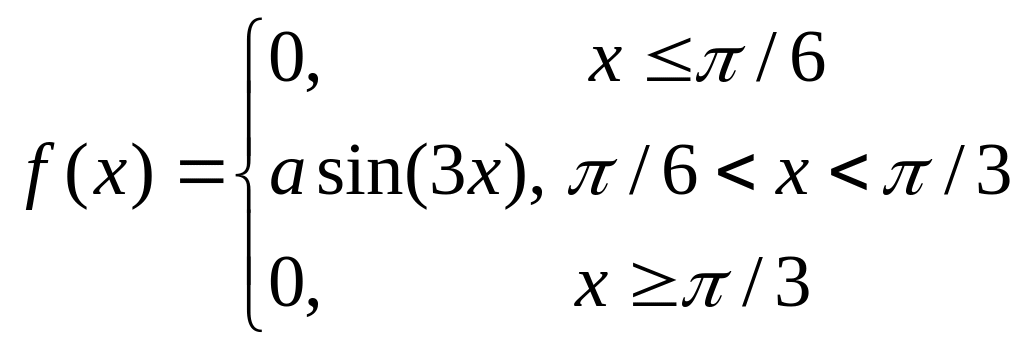Требуется а) найти значение a; б) найти функцию распределения ; в) построить графики и ; г) вычислить математическое ожидание, дисперсию, медиану и моду; д) вычислить вероятность того, что X примет значение, принадлежащее интервалу .

Решение. а) Так как при и при , то равенство (2.33) принимает более простой вид: . Так как при , получаем

.

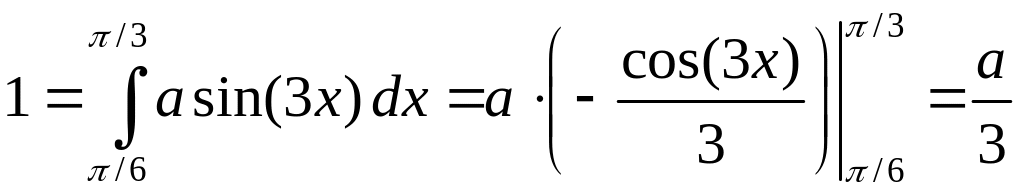Отсюда .

б) Используя формулу (2.31), найдем функцию распределения .

При имеем ,

так как при .

Если , то

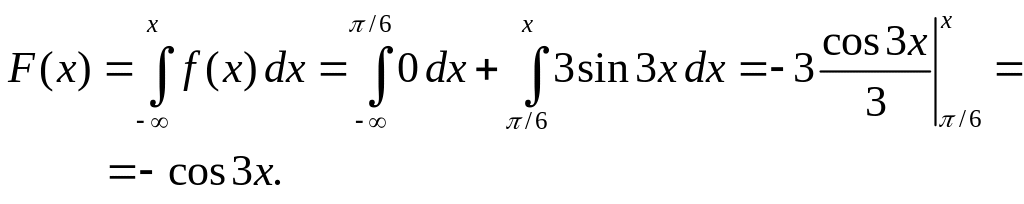
Если , то

.

Таким образом,

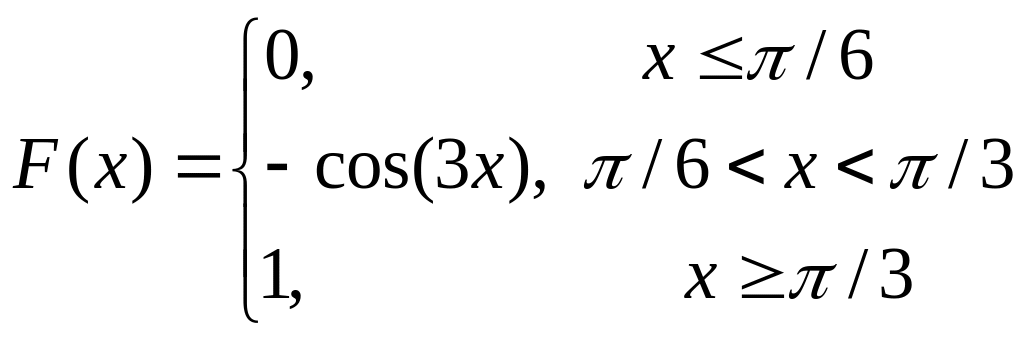. (2.38)

в) Построим графики и :

F(x)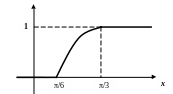

г) Вычислим математическое ожидание, используя формулу (2.34):

.

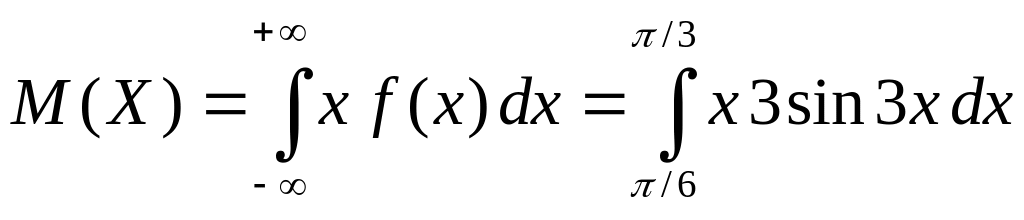Для вычисления последнего интеграла применим формулу интегрирования по частям: . Обозначим . Следовательно,

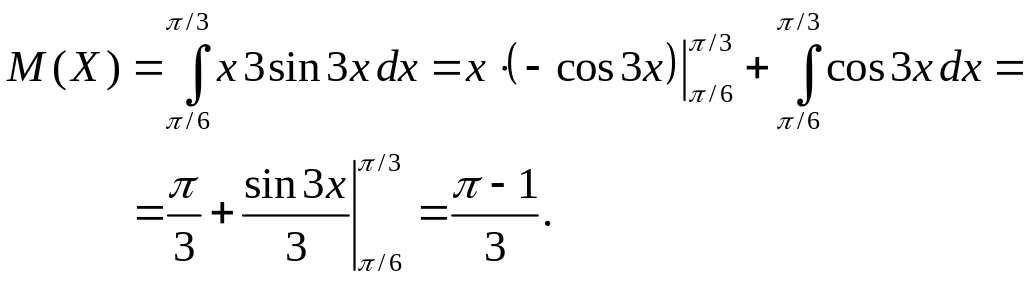
Вычислим дисперсию, используя формулу (2.36):

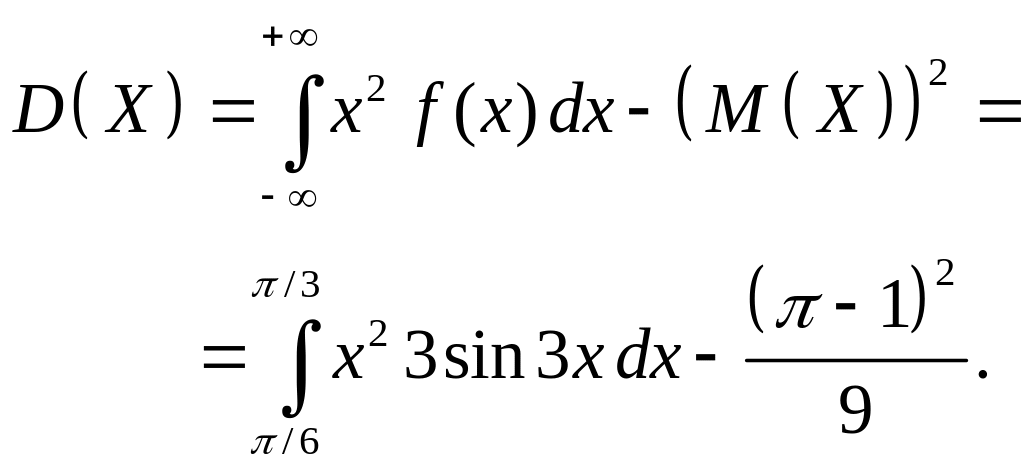(2.39)

Для вычисления интеграла в равенстве (2.39) применим формулу интегрирования по частям. Обозначим , . Тогда , . Следовательно,

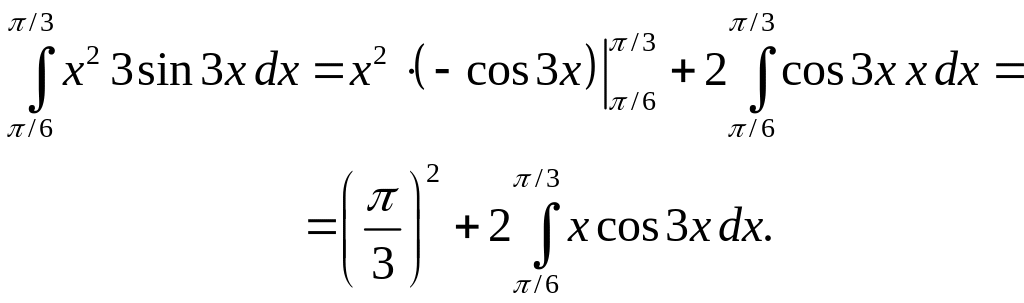(2.40)

Еще раз применим формулу интегрирования по частям к последнему интегралу:

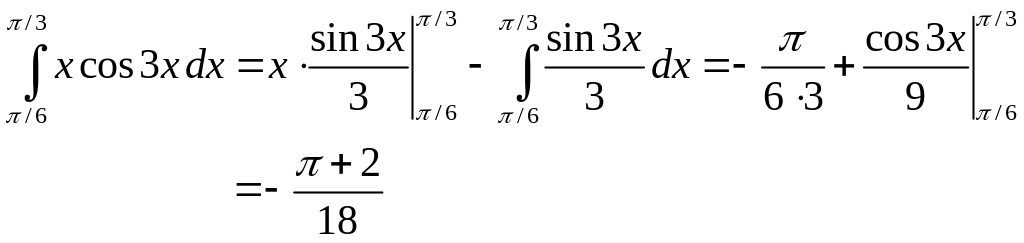
Подставим последний интеграл в равенство (2.40):

.

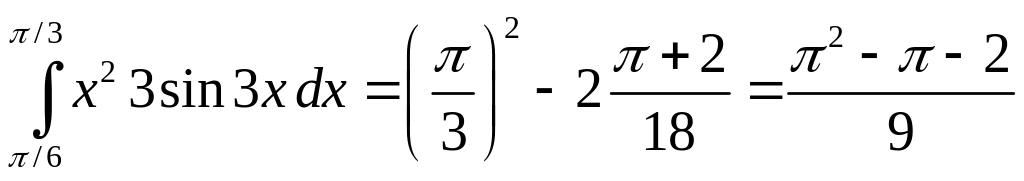Поэтому (см. равенство (2.39))

Найдем медиану , используя равенство . Следовательно, (см. формулу (2.38))

.

Поэтому, медиана равна .

Найдем моду , исходя из определения моды: . Но на интервале функция не имеет максимума, поэтому случайная величина X не имеет моды.

д) Вычислим вероятность , используя формулы (2.29) и (2.38):