2.7. Числовые характеристики дискретной случайной величины

2.7.1. Математическое ожидание

Определение 2.14. Математическим ожиданием дискретной случайной величины (см. раздел 2.4), принимающей возможные значения , ,…, с вероятностями , ,…, , соответственно, называется величина, равная сумме произведений всех ее значений на соответствующие им вероятности,

. (2.11)

Если число возможных значений бесконечно, то , причем ряд в правой части предполагается абсолютно сходящимся (в противном случае говорят, что случайная величина не имеет математического ожидания).

Свойства математического ожидания

1. для любой константы c.

2. для любой константы c.

3.

4. Для любых случайных величин X и Y справедливо следующее соотношение

. (2.12)

Замечание. Если дискретные случайные величины X и Y независимы (см. определение 2.5), то

для всех i, j. (2.13)

5. Для независимых случайных величин X и Y справедливо следующее соотношение

. (2.14)

Пример 2.3. Найти математическое ожидание случайной величины X, заданной в примере 2.1.

Решение. Применяя формулу (2.11), получим

.

Ответ: 2,8.

Пример 2.4. Найти математическое ожидание суммы числа очков, которые могут выпасть при бросании двух игральных костей.

Решение. Пусть случайные величины X и Y – это число очков, выпавших на первой и, соответственно, второй игральных костях. Тогда они имеют следующие законы распределения (см. пример 2.2):

X	1	2	3	4	5	6
P

Y	1	2	3	4	5	6
P

Тогда и

.

Следовательно, в силу формулы (2.12), получаем

.

Ответ: 7.

2.7.2. Дисперсия

Определение 2.15. Дисперсией дискретной случайной величины (см. формулу (2.4)), имеющей закон распределения , , называется величина

. (2.15)

Если число возможных значений бесконечно, то , причем ряд в правой части предполагается сходящимся (в противном случае говорят, что случайная величина не имеет дисперсии).

Свойства дисперсии

1. для любой константы c.

2. для любой константы c.

Замечание. Для вычисления дисперсии удобно использовать следующую формулу

. (2.16)

Следовательно, из формул (2.15) и (2.16) следует, что

. (2.17)

3. Для независимых случайных величин X и Y :

.

4. Для независимых случайных величин X и Y :

.

Пример 2.5. Найти дисперсию и среднее квадратическое отклонение случайной величины X, заданной в примере 2.1.

Решение. В примере 2.3 мы уже вычислили математическое ожидание величины X: . Применяя формулу (2.15), получим

.

В силу формулы (2.5), среднее квадратическое отклонение равно .

Ответ: , .

Пример 2.6. Дискретная случайная величина X распределена по закону

X	4	6
P	0,5	0,3

Зная, что , найти и , построить многоугольник распределения и вычислить дисперсию.

Решение. Используя уравнения (2.8) и (2.11), получаем

.

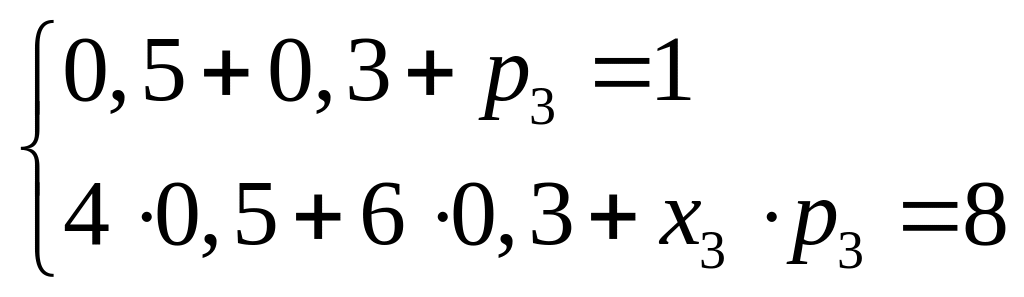
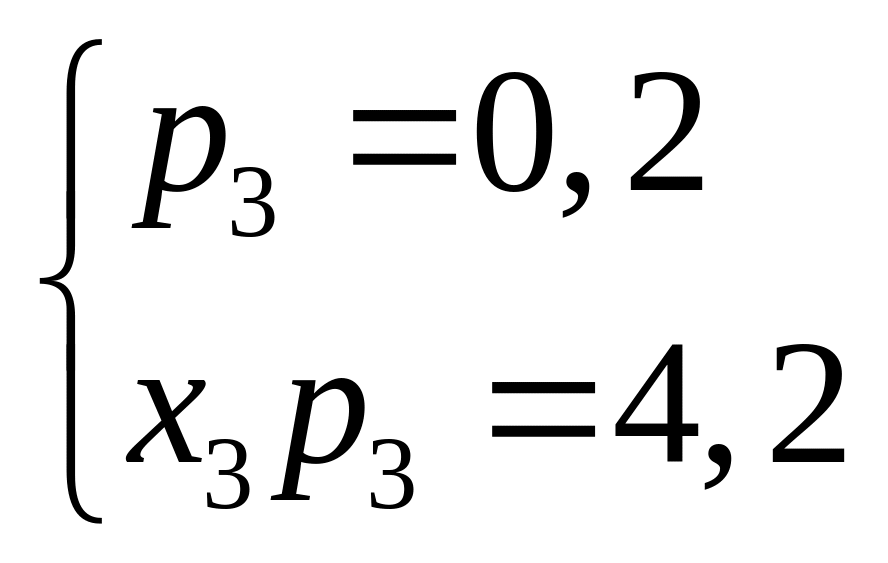
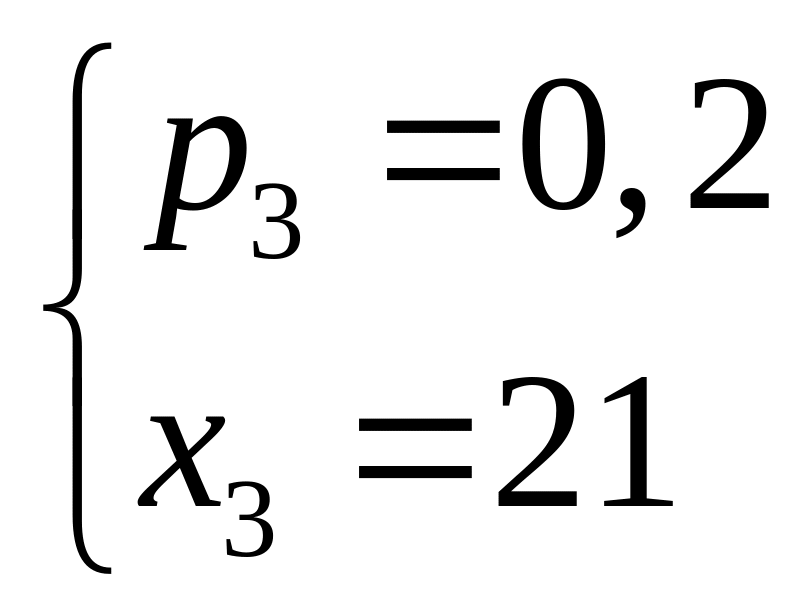Теперь построим многоугольник распределения:

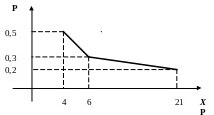
Найдем , используя формулу (2.15):

.

Ответ: , , .

Пример 2.7. Дискретная случайная величина X принимает три возможных значения , и , причем . Вероятности этих значений , , . Найти закон распределения X, если , .

Решение. Из формулы (2.8) следует, что . Поэтому . Следовательно, закон распределения X имеет вид

X	1
P	0,3	0,2	0,5

Найдем математическое ожидание:

.

По условию, . Следовательно,

. (2.18)

Кроме того, найдем :

.

Так как , получаем

. (2.19)

Объединяя уравнения (2.18) и (2.19), получаем

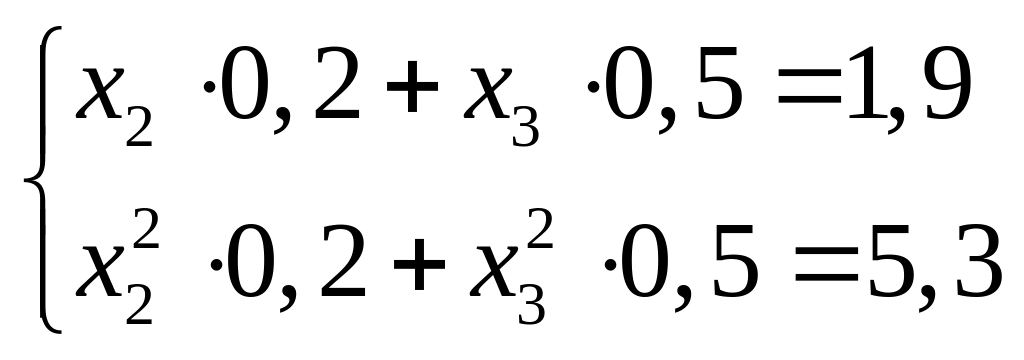
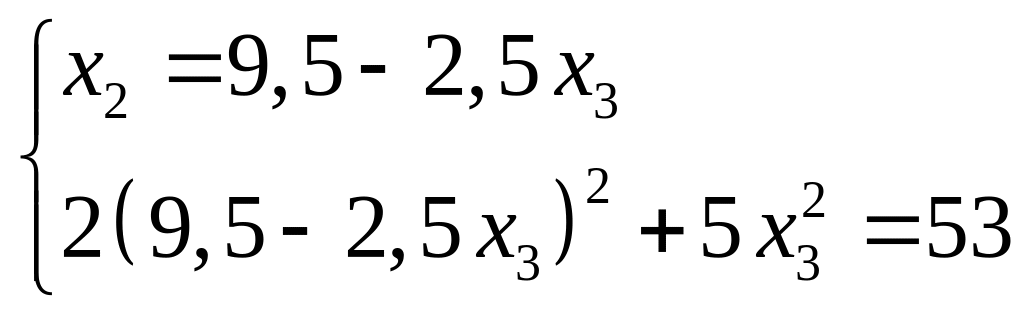
Решая эту систему, находим два решения , и , . По условию, , поэтому , .

X	1	2	3
P	0,3	0,2	0,5

Ответ:

Пример 2.8. Независимые случайные величины X и Y заданы следующим образом

X	2	3
P	0,1	0,9

Y	–1	1
P	0,6	0,4

Составить законы распределения случайных величин и и найти их математическое ожидание.

Решение. 1) Случайная величина принимает возможные значения , где , . Так как , , возможные значения . Действительно, , , , . Соответствующие вероятности вычисляются следующим образом: . Например, Z принимает значение только при , . Поэтому

.

Аналогично, Z принимает значение только при , . Поэтому

.

Если Z принимает свое значение при различных комбинациях значений X и Y, то вероятность получается сложением вероятностей отдельных комбинаций x и y, для которых . Например, Z принимает значение при , и при , . Поэтому

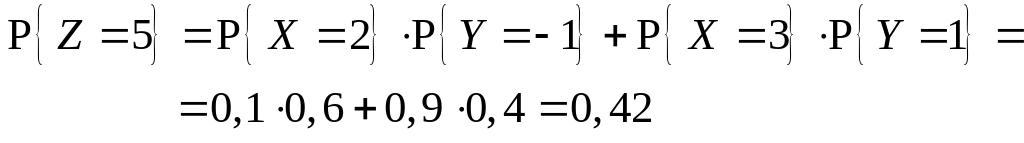
Следовательно, получаем закон распределения :

Z = 2 X- Y	3	5	7
P	0,04	0,42	0,54

Проверка: .

Теперь найдем , используя формулу (2.11):

.

Тот же результат получим, используя свойства математического ожидания (см. раздел 2.7.1):

,

так как

и .

2) Случайная величина принимает возможные значения , где , . Так как , , то возможные значения . Действительно, , , , . Соответствующие вероятности вычисляются следующим образом:

;

;

;

.

Следовательно, закон распределения имеет вид

Z = X Y	-3	-2	2	3
P	0,54	0,06	0,04	0,36

Проверка: .

Теперь найдем , используя формулу (2.11):

.

С другой стороны, тот же результат получим, используя формулу (2.14):

,

так как , .