2.5. Закон распределения дискретной случайной величины. Ряд и многоугольник распределения

Закон распределения дискретной случайной величины X удобно задавать с помощью формул

, ,

где , ,… – возможные значения величины X, а – вероятности их появления.

Другой способ задания дискретной случайной величины – в виде таблицы:

			…		…
			…		…

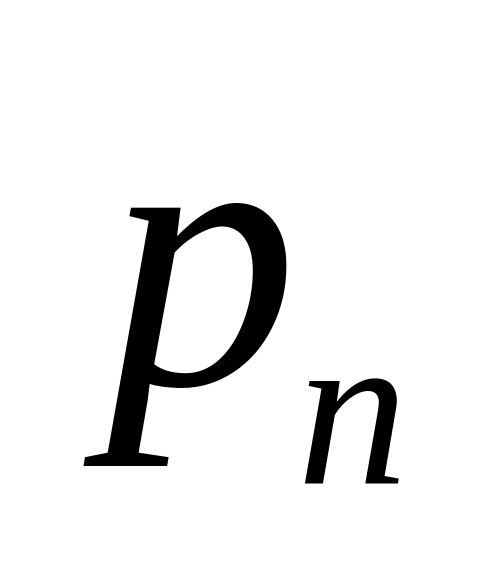
где в верхней строке перечислены все возможные значения , ,…, расположенные по возрастанию , а в нижней – их вероятности . Такая таблица называется рядом распределения.

Так как события , , …. несовместны и образуют полную группу событий, то справедливо следующее соотношение

. (2.8)

Закон распределения дискретной случайной величины X можно задавать также графически:

Ломаную, соединяющую точки , ,…, называют многоугольником (или полигоном) распределения.

Пример 2.1. Дискретная случайная величина X распределена по закону

X	1	3	5
P	0,3	0,5

Найти и построить многоугольник распределения.

Решение. Из формулы (2.8) вытекает, что . Следовательно, . Теперь построим многоугольник распределения:

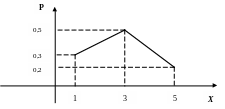
Заметим, что , поэтому мода величины X равна .

2.6. Функция распределения дискретной случайной величины

Функция распределения дискретной случайной величины имеет вид (см. формулу (2.2))

, (2.9)

Здесь суммирование ведется по всем i, для которых . Функция распределения любой дискретной случайной величины есть разрывная ступенчатая функция, скачки которой происходят в точках, соответствующих возможным значениям случайной величины. Применяя формулу (2.9), получаем

(2.10)

Например, если возможные значения случайной величины X есть , , , , то из определения (2.9) вытекает, что при , и при , и график функции распределения имеет вид

Стрелки на графике обозначают одностороннюю непрерывность слева в каждой точке .

Пример 2.2. Брошена игральная кость. Случайная величина X – число выпавших очков. Написать закон распределения величины X и построить ее функцию распределения .

Решение. Случайная величина X принимает возможные значения: {1, 2, 3, 4, 5, 6}. Вероятности этих значений , . Следовательно, ряд распределений X имеет вид:

X	1	2	3	4	5	6
P	1/6	1/6	1/6	1/6	1/6	1/6

Вычислим функцию распределения величины X, используя формулу (2.9) или (2.10):

Теперь построим график :