Глава 2. Случайные величины

2.1. Понятие случайной величины

Одним из важнейших понятий теории вероятностей (наряду с вероятностью и случайным событием) является понятие случайной величины.

Определение 2.1. Случайная величина – это величина, которая в результате опыта (или испытания со случайным исходом) принимает одно и только одно возможное значение, наперед не известное и зависящее от случайных причин.

Случайные величины будем обозначать заглавными латинскими буквами X, Y; а их возможные значения – соответствующими строчными буквами , , ,…., , , ,…

Примеры случайных величин

1. Испытание – бросок одной игральной кости. Случайная величина – число выпавших очков; ее возможные значения: {1, 2, 3, 4, 5, 6}.

2. Испытание – бросание монеты 2 раза. Случайная величина 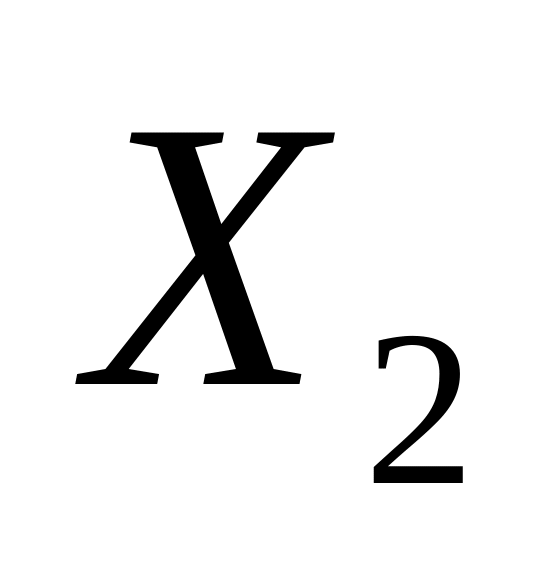– число выпадений «орла»; ее возможные значения: {0, 1, 2}.

3. Испытание – стрельба по мишени. Случайная величина 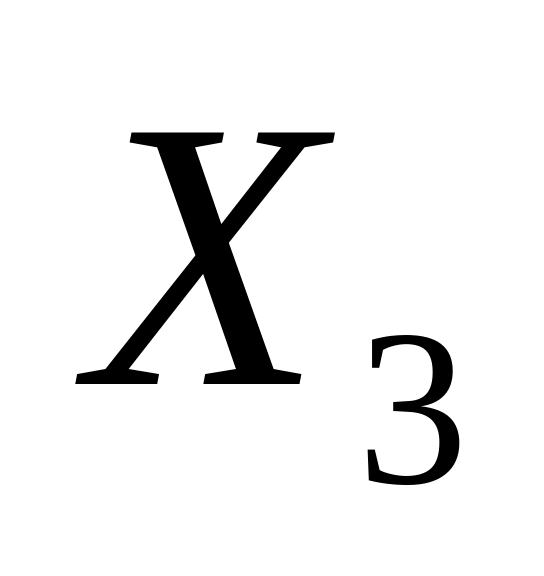– число выстрелов до первого попадания в цель; ее возможные значения: {1, 2, 3,…}.

4. Случайная величина 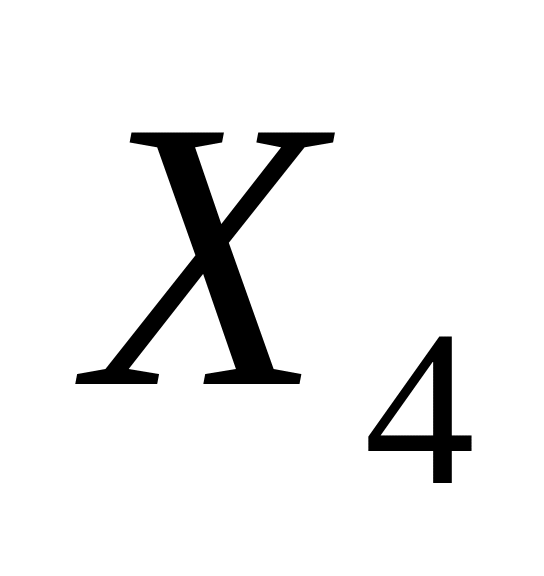– "температура воздуха, измеряемая на данной метеостанции в случайный момент времени в течение года"; ее возможные значения – .

5. Случайная величина – расстояние, которое пролетит снаряд при выстреле из орудия ее возможные значения – .

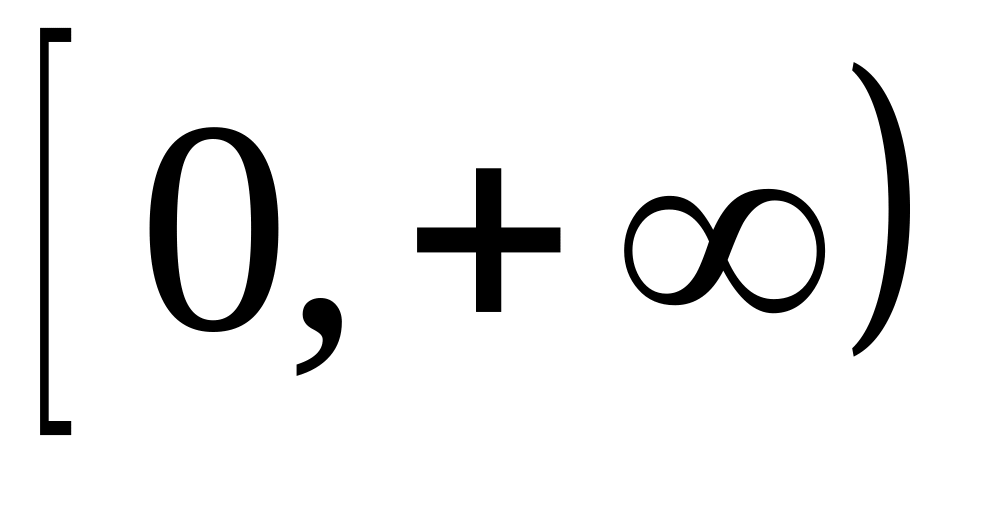В зависимости от вида множества возможных значений случайные величины могут быть дискретными и непрерывными.

Определение 2.2. Случайная величина Х называется дискретной, если она принимает отдельные изолированные возможные значения.

Число возможных значений дискретной случайной величины может быть конечным или счетным, т.е. их элементы можно расположить в определенном порядке и пронумеровать.

Определение 2.3. Случайная величина Х называется непрерывной, если она принимает любые значения из некоторого конечного или бесконечного промежутка.

Более строгое определение непрерывности случайной величины см. в разделе 2.9. Случайные величины , , из примеров выше – дискретные, а и – непрерывные.

2.2. Закон распределения вероятностей. Независимость случайных величин

Определение 2.4. Законом распределения случайной величины Х называется любая функция (правило, таблица, график и т.п.), устанавливающая соответствие между значениями случайной величины и вероятностями их наступления и позволяющая находить вероятности отдельных событий случайной величины или множества этих значений: для любых a и b.

Определение 2.5. Две случайные величины называются независимыми, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая величина.

Для независимых случайных величин выполнено следующее соотношение

для всех x, y. (2.1)

В том случае, когда это соотношение нарушается хотя бы в одной точке, величины X и Y называются зависимыми.

Замечание. Под понимается событие, состоящее в том, что случайная величина Х примет значение меньше, чем число x.

2.3. Функция распределения

Одним из способов задания закона распределения случайной величины является функция распределения вероятностей.

Определение 2.6. Функцией распределения вероятностей (или функцией распределения) случайной величины Х называется функция , равная вероятности того, что она примет значение меньше, чем аргумент функции x:

, . (2.2)