8. Ядро и образ линейного оператора.
Def.Ядром
линейного оператора
(обозначается
)
называется множество таких векторов
что
Def.Множество
векторов
называется
образом линейного оператора.
Обозначается
Th. 7.4 |
и
|
являются подпространствами линейного
пространства
Если
вектор-столбец координат вектора
в базисе
а
матрица линейного оператора
в этом базисе, то
тогда и только тогда, когда
Доказательство.
Пусть
тогда
Значит,
подпространство линейного пространства
Пусть
тогда, существуют
такие, что
и
Значит,
подпространство
линейного пространства
9. Евклидовы пространства. Неравенство Коши-Буняковского. Теорема Пифагора.
С помощью операций
и
,
введенных в линейном пространстве,
можно ввести понятие прямой, плоскости,
размерности, параллельности прямых
(плоскостей) и т.д. Однако, этих понятий
недостаточно, чтобы охватить все
многообразие фактов, составляющих
содержание евклидовой геометрии.
Например, мы не сможем дать определение
длины вектора, угла между векторами и
т.д. Ввести эти понятия попытаемся через
определение скалярного произведения
векторов.
Def.Скалярным
произведением
в линейном пространстве
над полем
называется функция двух векторных
аргументов
принимающая значения из
(обозначается
)
для которой выполняются следующие
аксиомы:
1.
2.
3.
4.
Причем
тогда и только тогда, когда
Def. Линейное пространство, на котором задано скалярное произведение, называется евклидовым пространством.
Неравенство Коши-Буняковского
Мы определили что
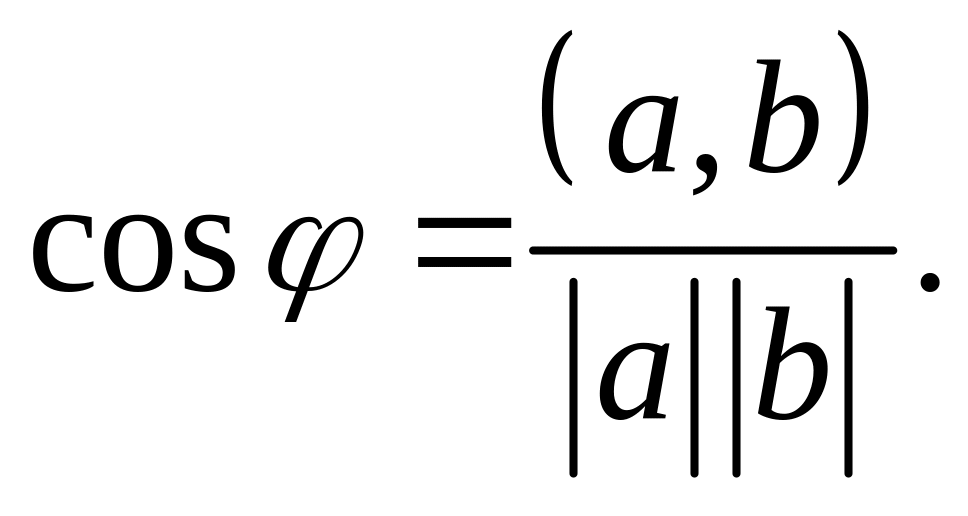Покажем, что такое определение корректно.
Для этого докажем, что
,
т.е.
Или
(5.5)
Неравенство (5.5) носит название неравенства Коши-Буняковского.
Доказательство.
Рассмотрим вектор
где
Согласно аксиоме 4 скалярного произведения
векторов
Преобразуем выражение, стоящее в левой части неравенства, на основании аксиом 1-3 скалярного произведения:
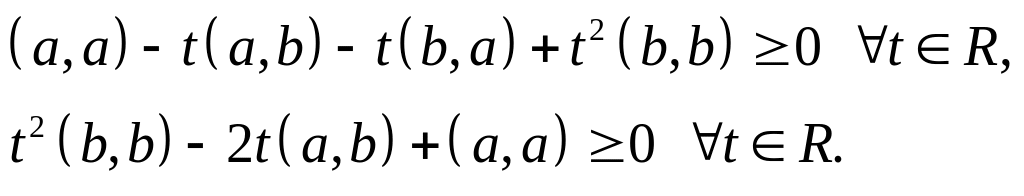
Значит, для
квадратного трехчлена, стоящего в левой
части неравенства,
Отсюда вытекает неравенство (5.5) .
В частности для евклидова пространства направленных отрезков это неравенство очевидно.
Для пространства
непрерывных на
функций неравенство
Коши-Буняковского
принимает вид
Следствие.
(неравенство треугольника)
Для любых
векторов
|
евклидова пространства справедливо
(5.6)Доказательство.
Отсюда
следует соотношение (5.6)
Th. 5.1 |
(теорема Пифагора)Если ортогональные векторы, то
|
(5.3)Доказательство.
.
10. Билинейные формы и их матрицы. Квадратичная форма.
Def.Говорят,
что в линейном пространстве
задана линейная
функция
(линейная
форма),
если
поставлено
в соответствие число
такое что:
1)
(11.1)
2)
(11.2)
Найдем выражение
линейной функции в координатах. Пусть
- базис
Согласно (11.1) и (11.2) имеем:
где
Таким образом, линейная функция представляется линейной формой:
(11.3)
Любая билинейная функция представляется билинейной формой:
где
(11.5)
Def.Матрица
где
называется матрицей
билинейной формы.
Рассмотрим как изменяется матрица билинейной формы при переходе к новому базису.
Пусть в базисе
билинейная форма имеет вид
где
И пусть
новый базис, в котором
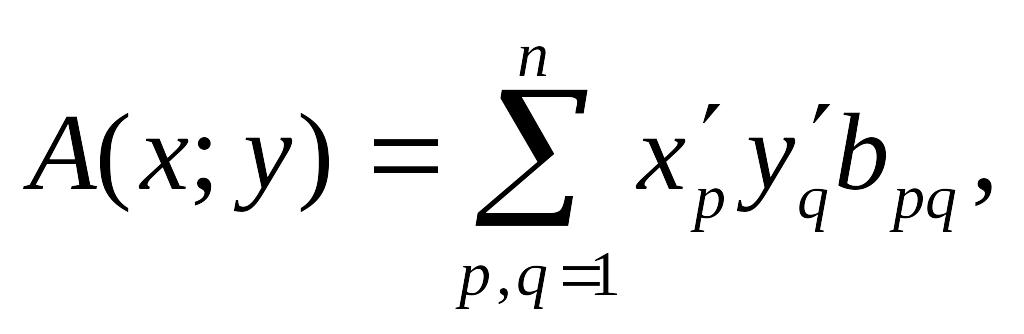где
В базисе
матрица билинейной формы
а в базисе
матрица билинейной формы
Пусть
матрица перехода от базиса
к базису
Обозначим
Тогда
Тогда
(11.6)
Это равенство в матричной форме имеет вид
,
(11.7)
где
матрица перехода от базиса
к базису
Def.Билинейная
форма
называется симметрической,
если
В этом случае
т.е. матрица билинейной формы
будетсимметрической. Верно и обратное.
Если матрица некоторой билинейной формы
симметрическая, то и билинейная форма
симметрическая.
Def.Если
в симметрической билинейной форме
положить
то получим квадратичную
форму
В этом случае билинейная форма
называется
полярной
к
Очевидно, чтоматрица квадратичной формы всегда симметрическая.
Th. 11.1 |
По квадратичной форме однозначно определяется породившая ее билинейная форма. |
Доказательство.
Пусть
Отсюда
(11.8)
Нахождение билинейной формы полярной к заданой квадратичной форме называется поляризацией квадратичной формы.
Из (11.5) следует, что любая квадратичная форма в заданном базисе задается формулой:
где
(11.9)