6. Линейные операторы, их матрицы и простейшие свойства.

Def. Пусть линейное пространство над полем Пусть задана функция называется линейным оператором, если выполняются следующие условия:

1) (свойство аддитивности оператора);

2) (свойство однородности оператора).

Обозначают или

Линейный оператор полностью задается заданием образов базисных векторов. Выберем в пространстве базис и применим к каждому из них оператор Полученные образы разложим по базису

(7.1)

Def.Матрица столбцы которой – координаты образов базисных векторов называется матрицей линейного оператора в базисе

Th. 7.1

Пусть вектор в базисе Тогда (7.2) где матрица линейного оператора в базисе

Доказательство.

Пусть тогда

.

7. Собственные векторы и собственные значения линейного оператора

Def. Пусть линейный оператор. Вектор называется собственным вектором линейного оператора если Число при этом называется собственным значением линейного оператора

Th. 8.3

В любом комплексном пространстве всякий линейный оператор имеет хотя бы один собственный вектор.

Доказательство.

Пусть базис матрица линейного оператора Пусть вектор-столбец координат вектора Вектор будет собственным вектором тогда и только тогда, когда

Отсюда

или

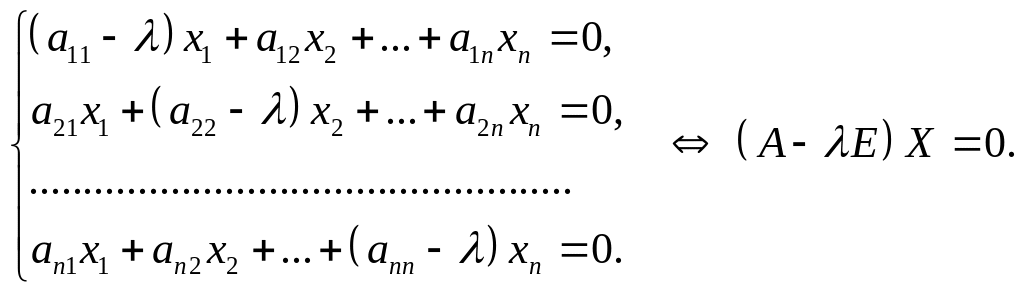(8.3)

Система линейных уравнений (8.3) имеет ненулевое решение тогда и только тогда, когда ее главный определитель равен нулю, т.е. когда

(8.4)

Уравнение (8.4) – уравнение й степени, а значит имеет по крайней мере один корень Подставив в систему (8.3) получим ее решение собственный вектор линейного оператора .

Def.Многочлен называется характеристическим многочленом линейного оператора а уравнение

(8.5)

– характеристическим уравнением линейного оператора

Th. 8.4

Характеристический многочлен (а, значит, и собственные значения) линейного оператора не зависит от выбора базиса

Доказательство.

Пусть матрица линейного оператора в базисе а матрица линейного оператора в базисе Согласно теореме 7.2

.

Def. Множество всех собственных значений называется спектром линейного оператора Обозначается

Th. 8.5

Пусть дано линейное пространство и линейный оператор, который имеет линейно независимых векторов. Если выбрать их в качестве базиса, то матрица оператора будет иметь диагональный вид. И наоборот, если в некоторм базисе матрица линейного оператора имеет диагональный вид, то все векторы этого базиса собственные.

Доказательство.

Пусть линейно независимые собственные векторы, тогда Тогда матрица оператора в этом базисе имеет вид:

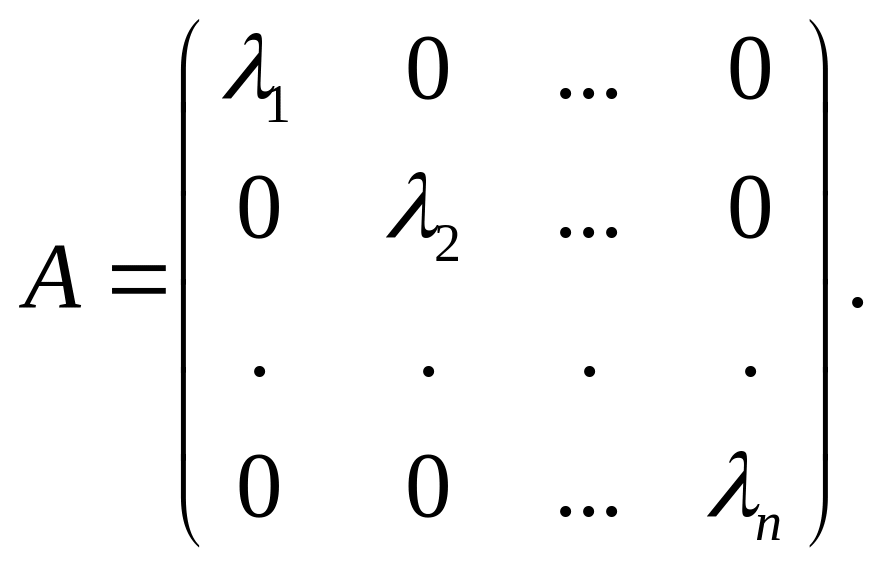
Обратное утверждение очевидно .

Th. 8.6

Если собственные векторы линейного оператора и соответствующие им собственные значения попарно различны, то линейно независимы.

Доказательство.

Применим метод математической индукции.

1) При утверждение очевидно.

2) Пусть утверждение верно для вектора. Докажем его справедливость для векторов. Пусть линейно зависимы, т.е.

(8.6)

Пусть для определенности Применим к обеим частям равенства (8.6) оператор

(8.7)

Домножим обе части равенства (8.6) на :

(8.8)

Вычтем из равенства (8.8) равенство (8.7), получим:

(8.9)

Т.к. то из равенства (8.9) следует линейная зависимость векторов что противоречит нашему предположению. Значит, утверждение теоремы справедливо .

Следствие.

Если характеристический многочлен линейного оператора имеет различных корней, то матрица этого оператора может быть приведена к диагональному виду, т.е. оператордиагонализируем.