4. Уравнение плоскости в пространстве

Уравнению первой степени на координатной плоскости соответствует в координатном простанстве уравнение

(14.1)

Th. 14.1

Каждое уравнение вида (14.1) определяет в пространстве плоскость наоборот, любая плоскость в координатном пространстве может быть задана уравнением (14.1)

Доказательство этой теоремы полностью моделирует доказательство соответсвующего утверждения для прямой на плоскости (проведите его самостоятельно, используя рис. 14.1).

Рис. 14.1

Рис. 14.2

Уравнение (14.1) называется общим уравнением плоскости, вектор – нормальным вектором плоскости.

Если плоскость проходит через точку перпендикулярно вектору (рис. 14.1), то ее уравнение можно записать в виде:

(14.2)

Плоскость однозначно определяется точкой и двумя векторами и ( неколлинеарны). Векторы и называются направляющими векторами плоскости. Пусть – текущая точка плоскости радиус вектор точки радиус-вектор точки (рис. 14.2).

тогда и только тогда, когда векторы компланарны. А поскольку неколлинеарны, то можно разложить по этим векторам, т.е. имеет место равенство:

Учитывая, что получаем:

(14.3)

Уравнение (14.3) называется векторным уравнением плоскости.

Т.к. тоуравнение (14.3) в координатной форме принимает вид:

(14.4)

Уравнения (14.4) называются параметрическими уравнениями плоскости.

Условие компланарности векторов можно выразить через смешанное произведение этих векторов: , или в координатной форме:

(14.5)

Уравнение (14.5) – уравнение плоскости, проходящей через точку с заданными направляющими векторами и

Плоскость однозначно определяется тремя точками не лежащими на одной прямой. В этом случае и – направляющие векторы плоскости Тогда из уравнения (14.5) получаем:

(14.6)

Уравнение (14.6) носит название уравнения плоскости, проходящей через три точки.

Пусть, в частности, известны точки, в которых плоскость пересекает оси координат: где (рис. 14.3) Тогда из уравнения (14.6) имеем:

Рис. 14.3

После раскрытия определителя получаем:

(14.7)

Уравнение (14.7) называется уравнением плоскости в отрезках на осях.

5. Корни многочлена и их кратность. Теорема Безу. Схема Горнера. Корни многочлена

Def. Пусть С[X] и – комплексное число. Положим Элемент называется корнем многочлена если

Th.1.6

(теорема Безу) Пусть – комплексное число и С[X]. Тогда остаток от деления на равен

Доказательство.

Делим на Получаем где

.

Следствие.

– корень многочлена тогда и только тогда, когда

Отметим, что если – комплексное число, то деля любой многочлен последовательно с остатком на получаем для разложение Тейлора

(1.11)

Изложим схему Горнера для быстрого вычисления коэффициентов в разложении Тейлора (1.11). Разделим на , получим

(1.12)

где Подставим выражение для в (1.12):

Приравняем коэффициенты при одинаковых степенях:

(1.13)

Формулы (1.13) позволяют быстро вычислить не используя операции возведения в степень, а с помощью лишь операций сложения и умножения. Результаты этих вычислений обычно записывают в виде таблицы

(1.14)

Таким образом, во второй строке полученной таблицы мы получаем коэффициенты многочлена и из (1.12). Такую форму записи вычисления указанных коэффициентов называют схемой Горнера.

Далее деля на и т.д., получаем:

			…
			…
			…
…	…	…	…	…	…

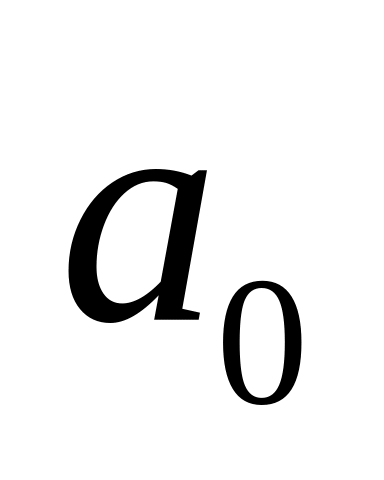
где - коэффициенты из формулы Тейлора (1.11).

Def. Корень многочлена называется корнем кратности если и не делится на Если кратность корня то корень называется простым корнем.

Th.1.7

Пусть С[X], Если – корень кратности многочлена то он является корнем кратности для многочлена

Доказательство.

Поскольку – корень кратности многочлена то

где

Очевидно, что Если то т.е. Противоречие. Значит, не делится на По определению – корень кратности для .

Следствия.

1. Элемент является корнем кратности многочлена тогда и только тогда, когда – общий корень и

2. Пусть Корнями многочлена являются толькократные корни Их кратность в на 1 меньше, чем в

Если - корни многочлена с кратностями соответственно, то

где не имеет корней. Поэтому справедливо утверждение

Th.1.8

Сумма числа корней многочлена (с учетом их кратности) не превосходит степени многочлена.