1. Обратная матрица и её свойства.

Обратная матрица

Def. Матрица А^-1 называется обратной к матрице А, если А^-1А=А А^-1=Е.

Def. Матрица А называется невырожденной, если , в противном случае она называется вырожденной.

Th.6.1

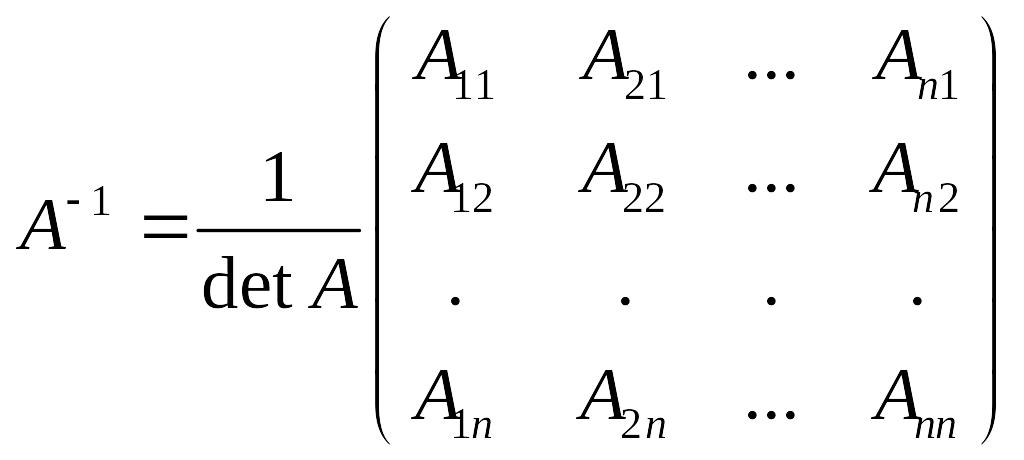
Любая невырожденная матрица имеет обратную, которая находится по формуле: (6.1) где - алгебраические дополнения к элементам матрицы

Доказательство.

Докажем, что вырожденная матрица не имеет обратной.

Пусть и . Тогда с одной стороны , а с другой стороны . Противоречие. Значит, для вырожденной матрицы не существует обратной.

Проверим, что матрица заданная формулой (5.1) действительно является обратной к А. Для этого убедимся, что А^-1А=А А^-1=Е.

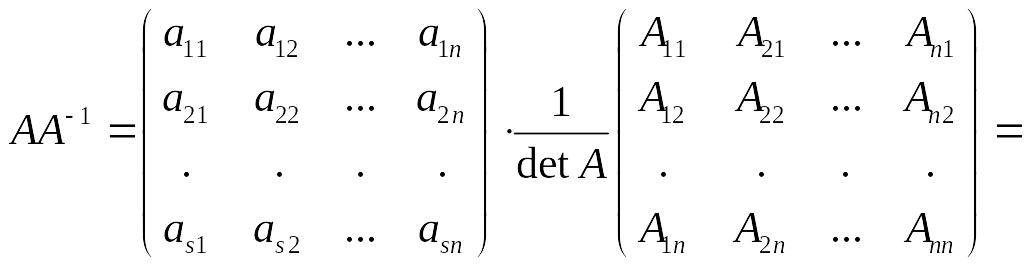
Найдем элемент матрицы В:

.

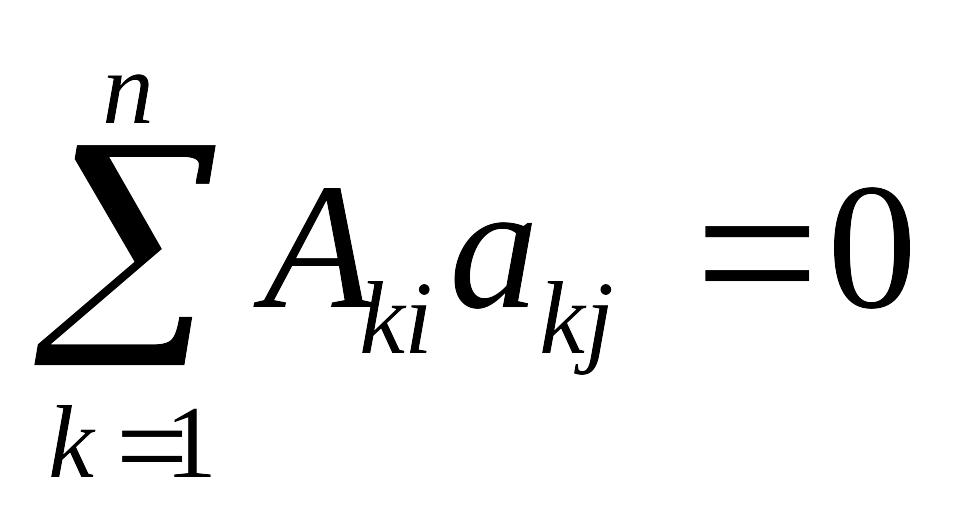Если то и Если же то и Таким образом,

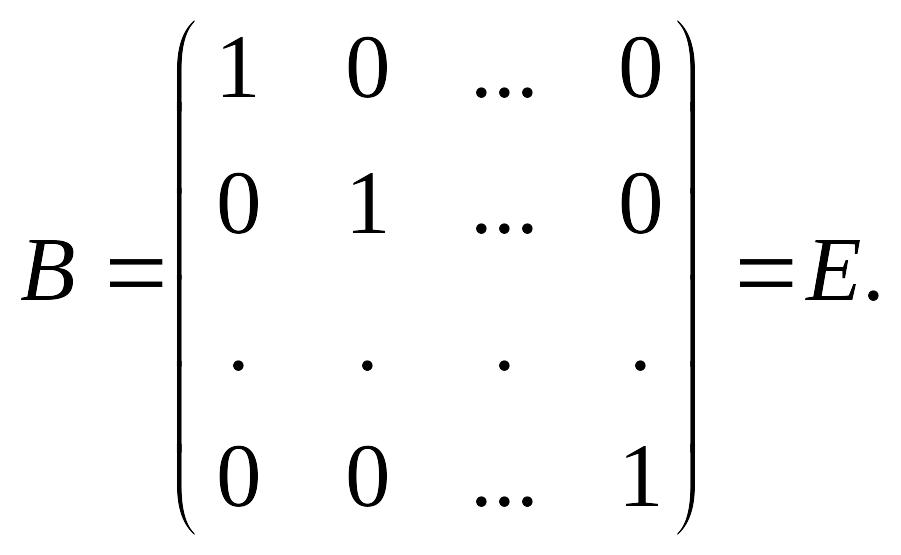
Аналогично доказываем, что

Свойства обратной матрицы:

. . .

Доказательство.

Свойство 1 вытекает непосредственно из определения.

Докажем свойство 2. По определению обратной матрицы .

. Поскольку то .

Докажем свойство 3.

.

.

По определению – обратная матрица для матрицы , т.е. .

Докажем свойство 4.

и Значит, по определению матрица – обратная матрица для , т.е.

2. Векторное n-мерное пространство

Def. Упорядоченный набор чисел , где называется n-мерным вектором; называются компонентами вектора .

Def. Два вектора и называются равными, если .

Def. Суммой двух векторов и называют вектор .

Def. Произведением вектора на число называется вектор . При этом векторы и называют пропорциональными.

Def. Под разностью векторов понимают .

Непосредственно из определений суммы векторов и произведения вектора на число вытекают следующие свойства этих операций:

1. (коммутативность); 2. (ассоциативность); 3. (нулевой вектор) такой, что ; 4. (противоположный вектор) такой, что ; 5. (дистрибутивность относительно умножения на вектор); 6. (дистрибутивность относительно умножения на число); 7. .

Def. Множество всех n-мерных векторов с введенными операциями сложения векторов и умножения на число так, как это сделано выше, называется n-мерным векторным пространством ( ).

Def. Линейным подпространством пространства называется любое его подмножество, замкнутое относительно операций сложения и умножения на число.

N. Множество векторов вида является линейным подпространством пространства .

3. Уравнение прямой на плоскости

Th. 13.1	Любая прямая на координатной плоскости может быть задана уравнением первой степени: (13.4) И, наоборот, любое уравнение первой степени определяет на плоскости прямую.
Доказательство. 1) Положение прямой однозначно определяется точкой которая принадлежит прямой, и вектором Будем называть этот вектор нормальным вектором прямой или нормалью. Т.к , то Выберем - текущую точку прямой		Рис. 13.1

Очевидно, что тогда и только тогда, когда или В координатной форме последнее равенство имеет вид:

(13.5)

После раскрытия скобок получаем , где Таким образом, первая часть утверждения теоремы доказана.

2) Пусть – одно из решений уравнения (13.4), т.е.

(13.6)

Вычтем из уравнения (13.4) уравнение (13.6), получим Это уравнение является координатной записью условия где Но это условие определяет прямую, которая проходит через точку М перпендикулярно вектору . Таким образом, доказано и второе утверждение теоремы .

Замечания.

1. Уравнение называется уравнением прямой, проходящей через точку перпендикулярно вектору

2. Уравнение (13.4) называют общим уравнением прямой. Коэффициенты перед переменными в общем уравнении прямой на плоскости имеют вполне определенный геометрический смысл: они являются координатами нормального вектора прямой.

3. Очевидно, что если в уравнении (13.4) то прямая проходит через начало координат.

4. Если в уравнении (13.4) то В этом случае прямая параллельна оси Аналогично, если в уравнении (13.4) то прямая параллельна оси