10. Экспоненциальная функция полезности. Пример.

.

Предположим, что лотерея описывается плотностью равномерного распределения на отрезке [x1; x2].

Найти ожидаемый выигрыш и детерминированный эквивалент.

Ожидаемый выигрыш равен , а детерминированный эквивалент определяется из уравнения:

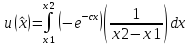
Если выигрыши лотереи увеличить на определенную сумму, то и детерминированный эквивалент увеличится на ту же самую сумму. Это является важным свойством экспоненциальной функции полезности.

11. Квадратичная функция полезности. Пример.

Убывающая функция полезности. Пусть u(x)=-x², x>=0. Найти ожидаемые выигрыши и детерминированные эквиваленты для лотерей L1=[0,0.5; 10,0.5] и L2=[10,0.5; 20,0.5] .

Решение: Ожидаемые выигрыши находятся по формуле

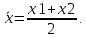Для L1 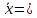5, L2 15.

Детерминированный эквивалент находится из уравнени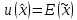я или для

L1: ; ;

L2: ; ;

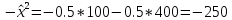Это означает, что принимающему решение безразлично получить ли 7,07 наверняка или участвовать в лотерее L1, получить ли 15,8 наверняка или участвовать в L2.

12. Теоремы о несклонности к риску. Надбавка за риск.

Теорема 2. ЛПР не склонен к риску тогда и только тогда, когда его функция полезности вогнута.

Следствие. ЛПР, который предпочитает получение наверняка ожидаемого выигрыша любой лотереи [x1,0.5; x2,0.5] (для любых неравных друг другу x1 и x2) участию в самой лотерее, не склонен к риску.

Теорема 4. При возрастающих функциях полезности ЛПР не склонен к риску тогда и только тогда, когда его детерминированный эквивалент для любой невырожденной лотереи меньше, чем ожидаемый выигрыш в этой лотерее.

Определение. Надбавкой за риск к лотерее называется разность между ее ожидаемым выигрышем и детерминированным эквивалентом:

.

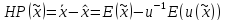Теорема 5. При возрастающих функциях полезности ЛПР не склонен к риску тогда и только тогда, когда надбавка за риск для него положительна для всех невырожденных лотерей.

Надбавка за риск – это сумма (в единицах измерения критерия X), которую принимающий решение согласен «уступить» из среднего выигрыша за то, чтобы избежать риска, связанного с данной лотереей.

13. Теоремы о склонности к риску. Надбавка за риск.

Теорема 3. ЛПР склонен к риску тогда и только тогда, когда его функция полезности выпукла.

Теорема 6. При возрастающих функциях полезности ЛПР склонен к риску тогда и только тогда, когда его детерминированный эквивалент для любой невырожденной лотереи больше, чем ожидаемый выигрыш в этой лотерее.

Надбавка за риск для возрастающих функций полезности определена как разность между ожидаемым выигрышем и детерминированным эквивалентом. Исходя непосредственно из этого определения, мы получаем теорему 7.

Теорема 7. При возрастающих функциях полезности ЛПР склонен к риску тогда и только тогда, когда надбавка за риск для него отрицательна для всех невырожденных лотерей.

14. Пример функции полезности для лпр несклонного к риску.

У лиц, не склонных к риску, психологические переживания в связи с потерей некоторой суммы денег являются более сильными, чем удовлетворение от выигрыша такой же суммы.

Это означает, что для такого ЛПР, обладающего богатством в размере х0 рублей, функция полезности должна удовлетворять условию:

u(x₀) - u(x₀ - Δх) > u(x₀ + Δх)- u(x₀),

где:

u(x₀) - u(x₀ - Δх) - отражает уменьшение полезности (то есть меру переживаний, неудовлетворения) из-за потери Δх  рублей,

u(x₀ + Δх) - u(x₀) - отражает увеличение полезности (то есть меру удовлетворения) от выигрыша такой же суммы Δх.

Данное условие выполняется, если функция полезности является "выпуклой вверх".

На нижеприведённом рисунке хорошо видно, что выпуклая вверх функция u(x)действительно отражает большую "чувствительность" ЛПР к возможным потерям, чем к выигрышам.

На графике изображена функция полезности ЛПР несклонного к риску. В данной ситуации при достижении детерминированного эквивалента (доход = 150 000) происходит перегиб функции, и рост полезности от увеличивающейся суммы дохода сильно замедляется.