
Среднее Заочное отделение / 4 семестр / Цифровые и микропроцессорные устройства / Методические указания и задания к курсовому проекту (ЦиМПУ)
.pdfМИНИСТЕРСТВО СВЯЗИ И ИНФОРМАТИЗАЦИИ РЕСПУБЛИКИ БЕЛАРУСЬ
Учреждение образования «ВЫСШИЙ ГОСУДАРСТВЕННЫЙ КОЛЛЕДЖ СВЯЗИ»
Кафедра инфокоммуникационных технологий
ЦИФРОВЫЕ И МИКРОПРОЦЕССОРНЫЕ УСТРОЙСТВА
Методические указания по выполнению курсового проекта для учащихся специальностей
2-45 01 33 – Сети телекоммуникаций 2-45 01 32 – Системы радиосвязи, радиовещания и телевидения
Минск
2015
УДК 81.332 ББК 32.97 Ц75
Рекомендовано к изданию кафедрой инфокоммуникационных технологий
13 января 2014 г., протокол №7
Составитель В. И. Богородов, преподаватель высшей категории
кафедры инфокоммуникационных технологий
Рецензент
Е. В. Новиков, доцент кафедры инфокоммуникационных технологий,
канд. техн. наук
Цифровые и микропроцессорные устройства: методические Ц75 указания по выполнению курсового проекта для учащихся специальностей 2-45 01 33 – Сети телекоммуникаций, 2-45 01 32 – Системы радиосвязи, радиовещания и телевидения / сост. В. И.
Богородов. – Минск : УО ВГКС, 2014. – 92 с.
ISBN 978-985-7002-15-3.
Приводятся методические указания по выполнению курсового проекта по цифровой схемотехнике. Рассматриваются принципы построения умножителей, сумматоров, компараторов и комбинационных программируемых сдвигателей.
Предназначено для учащихся и преподавателей колледжа.
|
УДК 81.332 |
|
ББК 32.97 |
ISBN 978-985-7002-15-3 |
© Учреждение образования |
|
«Высший государственный |
|
колледж связи», 2014 |
2
ВВЕДЕНИЕ
Курсовой проект по дисциплине «Цифровые и микропроцессорные устройства» выполняется учащимися специальностей 2-45 01 33 – Сети телекоммуникаций, 2-45 01 32 – Системы радиосвязи, радиовещания и телевидения третьего курса дневной формы обучения и третьего курса заочной и дистанционной формы обучения.
Целью курсового проекта является формирование начальных умений и навыков самостоятельного проектирования цифровых устройств, углубление и расширение знаний функционирования типовых узлов цифровых устройств.
Задания к курсовому проекту имеют разный уровень сложности. Задания по темам № 1...4 предполагают разработку принципиальных электрических схем цифровых устройств на микросхемах схемотехники КМОП отечественного производства по заданной структурной электрической схеме (второй уровень сложности). Задания по темам № 1...4 разработаны в семи вариантах. Номер варианта учащиеся определяют по данным таблицы 0.1 (номер варианта может быть задан преподавателем индивидуально). Задания по теме № 5 (третий уровень сложности) предполагают разработку структурной и принципиальной электрических схем цифрового устройства по заданным исходным данным. Задания по теме № 5 разработаны в пяти вариантах и выдаются преподавателем только индивидуально.
Курсовой проект должен состоять из трех листов, на которых выполняется логическая схема основного узла, принципиальная электрическая схема устройства и перечень элементов, а также пояснительной записки объемом 30…40 страниц формата А4. Текстовая и графическая части курсового проекта выполняются с помощью компьютерных средств. Требования к оформлению курсового проекта подробно изложены в [5], а кратко – в приложении В.
Примечания
1 Исходные данные для проектирования по темам № 1...4, выдаваемые преподавателем, могут отличаться от значений, указанных в таблицах 1.1, 2.1 и 3.1.
3
2 Курсовой проект, который выполнен без задания или по заданию без подписи преподавателя, на проверку не принимается.
3 На проверку учащиеся сдают чертежи, распечатку пояснительной записки и электронный вариант курсового проекта (текстовую часть – в формате .RTF, а графическую часть – в
формате .dwg (AutoCAD 2006 или AutoCAD 2008). Электронный вариант представляет собой папку, в которой титульный лист, задание, разделы курсового проекта и чертежи являются отдельными документами. На диске следует маркером указать фамилию учащегося, шифр группы и номер варианта.
4 В распечатку пояснительной записки следует подшивать рукописный вариант задания, подписанный преподавателем, и распечатку электронного варианта задания. Примеры оформления заданий приведены в приложении Б.
Таблица 0.1 – Номера вариантов заданий к курсовому проекту
Номер по списку для ДФО |
Номер варианта задания |
|
или номер зачетки для |
||
к курсовому проекту |
||
ЗФО |
||
|
||
1 |
2 |
|
1 |
1.1 |
|
2 |
2.1 |
|
3 |
3.1 |
|
4 |
4.1 |
|
5 |
1.2 |
|
6 |
2.2 |
|
7 |
3.2 |
|
8 |
4.2 |
|
9 |
1.3 |
|
10 |
2.3 |
|
11 |
3.3 |
|
12 |
4.3 |
|
13 |
1.4 |
|
14 |
2.4 |
|
15 |
3.4 |
|
4 |
|

Окончание таблицы |
0.1 |
|
|
|
|
1 |
|
2 |
16 |
|
4.4 |
17 |
|
1.5 |
|
|
|
18 |
|
2.5 |
19 |
|
3.5 |
20 |
|
4.5 |
21 |
|
1.6 |
22 |
|
2.6 |
23 |
|
3.6 |
24 |
|
4.6 |
25 |
|
1.7 |
26 |
|
2.7 |
27 |
|
3.7 |
28 |
|
4.7 |
29 |
|
5.1 |
30 |
|
5.2 |
31 |
|
5.3 |
32 |
|
5.4 |
33 |
|
5.5 |
Примечание – Первая цифра слева в номере варианта задания означает номер темы, а вторая – номер варианта внутри темы.
1 ТЕМА № 1. УСТРОЙСТВО УМНОЖЕНИЯ ДВОИЧНЫХ ЧИСЕЛ
1.1 Описание принципа работы заданной структурной электрической схемы устройства умножения двоичных чисел
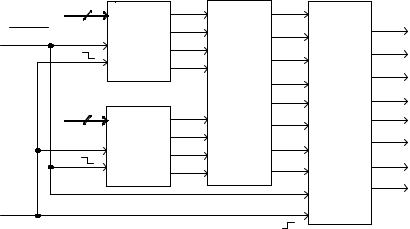
Структурная электрическая схема устройства умножения четырехразрядных двоичных чисел представлена на рисунке 1.1.
5
|
|
|
4 |
Y1 |
a |
|
Y3 |
q |
|
Y4 |
|
|
|
А |
|
Регистр |
0 |
Умножи- |
0 |
Регистр |
|
||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
a |
... |
a |
0 |
1 |
тель |
q |
1 |
q |
|
||
RESET |
|
3 |
|
|
a |
|
0 |
|||||
|
|
|
|
|
2 |
|
|
|
|
|||
|
|
|
|
|
|
|
q |
|
q |
|
||
U |
|
|
|
|
|
|
|
2 |
1 |
|||
|
|
|
|
|
a |
|
|
|||||
|
|
|
|
|
|
|
|
|||||
R |
|
|
|
|
|
3 |
|
|
|
|
||
|
|
|
|
|
|
|
|
q |
|
q |
|
|
|
|
|
|
|
|
|
|
|
3 |
2 |
||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
Y2 |
|
|
|
q |
4 |
q |
3 |
|
|
|
4 |
|
b |
|
|
|
||||
|
|
|
|
Счетчик |
0 |
|
q |
|
|
|||
|
B |
|
|
|
5 |
q |
|
|||||
|
|
|
|
b |
|
4 |
||||||
|
|
|
|
|
|
|
|
|||||
|
b |
3 |
... b |
0 |
1 |
|
|
|
|
|||
|
|
|
|
|
|
|||||||
|
|
|
q |
|
q |
|
||||||
|
|
|
|
b |
|
|
6 |
5 |
||||
|
|
|
|
|
|
2 |
|
|||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
b |
3 |
|
7 |
q |
6 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
q |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
CLOCK |
|
|
|
|
|
|
|
|
|
|
|
|
U |
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 1.1 – Устройство умножения двоичных чисел. Схема электрическая структурная
Рассмотрим назначение узлов, входящих в структурную схему устройства.
Умножитель Y3 предназначен для умножения четырехразрядных двоичных чисел A и B, представленных разрядами a0, a1, a2, a3 и b0, b1, b2, b3. На выходе умножителя формируется восьмиразрядное произведение Q, представленное разрядами q0, q1,...,q7.
Регистр Y1 предназначен для параллельного ввода четырехразрядного множимого A в двоичной системе счисления (СС). Значение множимого A может меняться в пределах от 0 до 15 в десятичной СС.
Счетчик Y2 предназначен для параллельного ввода четырехразрядного множителя B в двоичной СС. Значение множителя B также может меняться от 0 до 15 в десятичной СС.
Регистр Y4 предназначен для параллельного вывода результата умножения, который представляет собой восьмиразрядное кодовое слово.
Загрузка сомножителей и запись результата умножения синхронизируется тактовыми импульсами UC . Причем ввод
6
сомножителей осуществляется по отрицательным фронтам тактовых импульсов, а вывод результата умножения – по положительным.
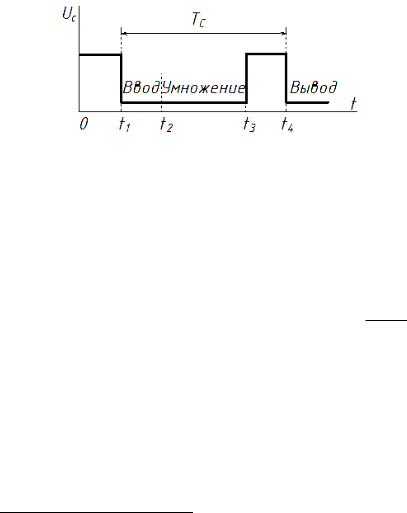
Процесс функционирования устройства поясняется временной диаграммой, которая представлена на рисунке 1.2.
Рисунок 1.2 – Временная диаграмма, поясняющая процесс функционирования устройства умножения
В момент времени t1 по отрицательному фронту тактового импульса (рисунок 1.2) начинается ввод сомножителей в регистр Y1 и счетчик Y2 (рисунок 1.1). К моменту времени t2 ввод заканчивается, и начинается процесс умножения в умножителе Y3. Этот процесс в худшем случае завершается к моменту времени t3. Затем по положительному фронту тактового импульса результат умножения записывается в регистр Y4 и т. д.
При подаче низкого уровня напряжения на вход |
RESET |
(рисунок 1.1) устройство сбрасывается в исходное нулевое состояние.
Рассмотрим процесс |
умножения |
двоичных |
чисел на |
||
примере |
умножения |
заданных |
|
чисел1), |
например: |
A 13(10) |
1101(2) и |
B 11(10) |
1011(2) . |
Умножение |
|
выполним, начиная с младшего разряда множителя:
1) В пояснительной записке следует приводить пример умножения для чисел A и B согласно заданному варианту.
7

|
|
|
|
a3 |
a2 |
a1 |
a0 |
– множимое |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
0 |
1 |
|
|
|
|
|
|
× |
|
|
|
|
|
|
|
|
|
1 |
0 |
1 |
1 |
|
|
|
|
|
|
b3 |
b2 |
b1 |
b0 |
– множитель |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
1 |
1 |
0 |
1 |
|
|
|
|
+ |
1 |
1 |
0 |
1 |
|
|
|
|
+ |
0 |
0 |
0 |
0 |
|
|
|
– частичные |
|
|
|
|
произведения |
|||||
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
– полное |
|
q7 |
q6 |
q5 |
q4 |
q3 |
q2 |
q1 |
|
|
произведение |
Таким образом, при умножении двоичных чисел формируются частичные произведения, сдвигаются и суммируются.
Сравним результаты умножения чисел A и B в двоичной и десятичной СС. Для этого преобразуем результат умножения в десятичную систему счисления:
10001111 |
1 2 |
7 |
0 2 |
6 |
0 2 |
5 |
0 2 |
4 |
1 2 |
3 |
1 2 |
2 |
1 |
|
|
|
|
|
|
|
|
1 2 |
|||||||||
(2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2 |
0 |
128 8 4 2 1 143 . |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
(10) |
|
|
|
|
|
Результаты совпадают и равны
143(10)
.
1.2Задание на проектирование к теме № 1
Описать принцип построения и разработать логическую
схему |
матричного |
умножителя |
четырехразрядных |
||
двоичных |
чисел. |
|
Разработать |
логическую |
схему |
суммирующего |
четырехразрядного |
счетчика |
на |
||
JK-триггерах с коэффициентом пересчета Кпер, заданным в таблице 1.1. Разработать в основном базисе логическую схему
8

двухразрядного двоичного сумматора с параллельным переносом. Разработать принципиальную электрическую схему устройства умножения по заданной структурной схеме (рисунок 1.1) на микросхемах схемотехники КМОП, серии которых указаны в таблице 1.1.
Таблица 1.1 – Исходные данные для проектирования устройства
|
умножения двоичных чисел |
|
|
|
||
|
|
|
|
|
|
|
Номер |
Значение |
Значение |
Серии |
|
|
|
числа A |
числа B |
K |
пер |
|||
варианта |
микросхем |
|||||
|
||||||
(P=10) |
(P=10) |
|
|
|||
|
|
|
|
|||
1.1 |
13 |
12 |
1594, 5564 |
11 |
||
1.2 |
14 |
13 |
1554, 1564 |
13 |
||
1.3 |
12 |
14 |
1594, 5564 |
15 |
||
1.4 |
11 |
12 |
1554, 1564 |
9 |
||
1.5 |
14 |
13 |
1594, 5564 |
11 |
||
1.6 |
13 |
11 |
1554, 1564 |
13 |
||
1.7 |
11 |
12 |
1594, 5564 |
15 |
||
Описать работу принципиальной электрической схемы устройства в течение одного периода сигнала синхронизации Uc при умножении заданных в таблице 1.1 чисел A и B. Пример оформления задания к теме
№1 приведен в приложении Б.
1.3Назначение и принцип построения матричных умножителей двоичных чисел
Умножителем называется комбинационное цифровое устройство, формирующее на выходе число Q, равное произведению входных двоичных чисел A и B [9, 10].
Условное графическое обозначение (УГО) умножителя представляет собой прямоугольник с аббревиатурой MPL (от англ. Multiplier) во внутреннем поле (рисунок 1.3).
9

A
B
...
...
a |
0 |
|
|
a |
1 |
|
|
. . . |
|
a |
n-1 |
|
|
b |
0 |
|
|
b |
1 |
|
|
. . . |
|
b |
m-1 |
|
MPL |
q |
0 |
|
||
|
|
|
|
q |
1 |
|
|
. . .
q |
n+m-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
... |
|
|
|
Q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 1.3 – Условное графическое обозначение умножителя
Предполагается, что числа A, B и Q представлены в двоичной позиционной системе счисления. При этом, если число A имеет n двоичных разрядов (a0, a1,…, an-1), число B имеет m
двоичных |
|
разрядов |
(b0, b1,…, |
||
bm-1), то для представления |
максимального значения |
||||
произведения |
n |
1) (2 |
m |
1) |
требуется n+m двоичных |
AB (2 |
|
||||
разрядов числа Q (q0, q1,…, qn+m-1). Каждый разряд произведения является логической (переключательной) функцией аргументов a0, a1,…, an-1 и b0, b1,…, bm-1, значения которого можно найти из таблиц умножения либо путем выполнения умножения для заданных значений аргументов. Однако прямой логический синтез схемы умножителя, основанный на представлении функции выражениями в булевой алгебре, ввиду громоздкости неэффективен. Исключения составляют простейшие случаи перемножения одноразрядных или двухразрядных двоичных чисел. Поэтому на практике используют методы синтеза, основанные на разложении операции умножения на последовательность простейших арифметических действий с одноразрядными числами. Полагая, что в двоичном
10
