
Среднее Заочное отделение / 4 семестр / Цифровые и микропроцессорные устройства / Электронный конспект лекций (ЦиМПУ)
.pdfУЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ
«БЕЛОРУССКАЯ ГОСУДАРСТВЕННАЯ АКАДЕМИЯ СВЯЗИ»
Конспект лекций
по дисциплине «Цифровые и микропроцессорные устройства»
Составитель: |
В.И. Богородов |
Утвержден на заседании кафедры ИКТ
Протокол № 1 от 03.11.2015 г.
Зав. кафедрой Новиков В.И
Минск
2015
ВВЕДЕНИЕ
Дисциплина «Цифровые и микропроцессорные устройства» занимает особое место в подготовке техников связи. Это связано с тем, что цифровые и вычислительные методы и устройства широко используются в системах, осуществляющих сбор, передачу, хранение, распределение и обработку информации. Эти методы и устройства используются в связной, измерительной, диагностической и другой аппаратуре. Широкое применение цифровой техники резко увеличивает спрос на специалистов соответствующего профиля.
Конспект лекций составлен в соответствии с типовой учебной программой дисциплины «Цифровые и микропроцессорные устройства» для учащихся УО ВГКС на основе учебного пособия [1] и состоит из трех разделов.
Впервом разделе рассматривается арифметические, логические и схемотехнические основы цифровой техники, а также основы теории синтеза цифровых устройств. Теоретический материал подкрепляется примерами выполнения арифметических и логических операций, а также примерами логических функций и построения несложных логических схем.
Во втором разделе рассматриваются способы схемотехнической реализации логических функций, а также типовые функциональные узлы комбинационных
ипоследовательностных цифровых устройств и общие принципы организации контроля цифровых устройств. Приводятся примеры микросхем стандартной логики.
Втретьем разделе рассматриваются типовые структуры микропроцессорных вычислительных систем, назначение и взаимодействие отдельных узлов, а также принцип микропрограммного управления.
Основной материал данного раздела основан на рассмотрении классического простого 8-разрядного микропроцессора Intel 8085A и современного 16разрядного микроконтроллера dsPIC33F, который поддерживает команды цифровой обработки сигналов. Рассматриваются их архитектура, организация памяти, основные модули, система команд и основы программирования. Кроме того, в данном разделе рассматриваются типы и схемотехника запоминающих устройств, а также интерфейсных схем.
2
РАЗДЕЛ 1 ОСНОВЫ ЦИФРОВОЙ ТЕХНИКИ
Тема 1.1 Арифметические основы цифровой техники
1.1.1 Системы счисления. Основные понятия. Выбор системы счисления для цифровых устройств
Система счисления (СС) – это совокупность приемов и правил изображения чисел цифровыми знаками. Системы счисления делятся на позиционные и непозиционные.
В непозиционных СС значение символа не зависит от его положения в числе, причем применяется неограниченное количество символов. Непозиционные СС используются редко, в основном для целей нумерации. Примером такой системы является римская СС с символами:
Десятичные числа |
1 |
5 |
10 |
50 |
100 |
500 |
1000 |
и т. д. |
Римские символы |
I |
V |
X |
L |
C |
D |
M |
и т. д. |
Несколько стоящих рядом одинаковых символов суммируются: XXX = X + + X + X = 30. Если рядом стоят два разных символа, причем младший – справа от старшего, то они также суммируются: XVI = X + V + I = 16. Если же младший символ находится слева от старшего, то он вычитается, из этого старшего символа: IX = X – I = 9.
Основной недостаток непозиционных СС – большое число различных символов, громоздкость чисел и сложность выполнения арифметических операций.
В позиционных СС значение символа зависит от его позиции в последовательности символов, изображающих число. Например, в десятичном числе 33 первая цифра слева означает количество десятков, вторая – количество единиц. В позиционных СС используется ограниченное количество символов, они более удобны для вычислительных операций, поэтому получили наибольшее распро-
странение. Количество различных символов, используемых для изображения всех чисел в пределах одного разряда, называется основанием позиционной СС.
Любое число X, записанное в позиционной СС, можно представить в виде полинома:
3

X(P) = anPn + an-1Pn-1 + … + a0P0 + a-1P-1 + … + a-mP-m
целая часть 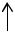 дробная часть
дробная часть
положение точки
=
i n |
i |
|
aiP |
||
|
||
i m |
|
,
(1.1)
где P – основание позиционной СС – целое положительное число; ai – любая цифра (символ), используемая в данной позиционной СС из множества {0,1, …, P-1}; Pi – весовой коэффициент разряда.
Индекс в круглых скобках указывает на величину основания СС. Точка, отделяющая целую часть числа от дробной, находится между разрядами с весовыми коэффициентами .
Например, десятичное число Х1 = 43.25 по формуле (1) имеет вид:
X1 = 43.25(10) = 4∙101 + 3∙100 + 2∙10-1 + 5∙10-2.
На величину основания позиционной СС нет ограничения. Поэтому возникает вопрос, какая величина основания P является оптимальной для применения в цифровых устройствах.
Наилучшая система счисления должна обеспечивать простоту технической реализации, простоту выполнения арифметических операций, малые затраты оборудования при построении устройств, высокую помехоустойчивость кодирования цифр и простоту применения математического аппарата для анализа и синтеза цифровых устройств. Краткий анализ систем счисления показывает, что для построения аппаратных средств цифровых устройствах следует применять двоичную СС.
В двоичной СС (P = 2) используются два символа – это цифры 0 и 1. Любое число в двоичной СС записывается в виде последовательности нулей и единиц, расставленных согласно формуле (1.1). Например, уже рассмотренное нами десятичное число Х1 = 43.25 в двоичной СС запишется следующим образом:
X1 = 101011.01(2) = 1∙25 + 0∙24 + 1∙23 + 0∙22 + 1∙21 + 1∙20 + 0∙2-1 + 1∙2-2 = 32 + 0 + +8 + 0 + 2 + 1 + 0 + 0.25 = 43.25(10).
Двоичная СС имеет один недостаток: в ней трудно оценить величину чисел, следовательно, ее использование приводит к необходимости преобразования исходных десятичных чисел в двоичную СС, а результатов – из двоичной в де-
4

сятичную СС. Для таких преобразований чисел требуются достаточно сложные аппаратные средства и дополнительное время. Для преодоления этого недостатка применяется двоично-десятичная СС, представляющая собой СС с основанием P = 10, цифры которой закодированы в виде четырехразрядных двоичных чисел (тетрад). Четырехразрядное двоичное число позволяет получить 24 16 наборов, из которых при двоично-десятичном кодировании используются только 10. Поэтому возможны различные варианты кодирования десятичных цифр в двоичной СС. Наибольшее распространение получил код 8421 – BCD-код (от англ. Binary Coded Decimal). Цифры 8421 указывают вес соответствующего двоичного разряда двоично-десятичного числа. Например, десятичное число X1 = 43.25 в коде 8421 запишется следующим образом:
X1 = 43.25(10) = 0100 0011.0010 0101 (2–10). 4 3 2 5
Для преобразования десятичных чисел в код 8421 и обратно используются простые типовые узлы цифровой техники, такие как шифраторы и дешифра-
торы.
Двоично-десятичные СС используются как для ввода/вывода, так и для обработки числовых данных.
В технике программирования в качестве вспомогательной широкое применение получила шестнадцатеричная СС, у которой основание P = 16, т. е. используется 16 символов – это цифры от 0 до 9 и шесть заглавных букв латинского алфавита: A, B, C, D, E, F. У этой СС основание является целой степенью числа 2, в результате по аналогии с двоично-десятичной СС ее можно определить как систему с основанием P = 16 , у которой символы закодированы в двоичной СС, что значительно облегчает перевод шестнадцатеричных чисел в дво-
ичную СС и обратно. Для преобразования шестнадцатеричного числа в двоичную систему счисления достаточно перевести в двоичную СС каждый символ исходного числа и записать их в виде тетрад. Например, преобразуем шестна-
дцатеричное число X = 7B.6F в двоичную СС:
X = 7B.6F(16) = 0111 1011 . 0110 1111(2).
7 B |
6 F |
5
Для обратного преобразования двоичное число разбивают на тетрады влево и вправо от точки, а затем содержимое каждой тетрады заменяют соответствующим символом шестнадцатеричной СС. Если левая и правая тетрады получаются неполными, то их следует дополнить нулями.
Шестнадцатеричная СС обеспечивает более компактную запись чисел и унификацию форматов числовой и командной информации в виде тетрад.
В заключение рассмотрим таблицу, в которой записаны десятичные числа от 0 до 17, представленные в различных СС (таблица 1.1).
Таблица 1.1 – Представление десятичных чисел в позиционных системах счисления
D (Decimal |
B (Binary |
H (Hexadecimal |
BCD (Binary-Coded |
notation) |
notation) |
notation) |
Decimal) |
P = 10 |
P = 2 |
P = 16 |
Код 8421 |
0 |
0000 |
0 |
0000 |
1 |
0001 |
1 |
0001 |
2 |
0010 |
2 |
0010 |
3 |
0011 |
3 |
0011 |
4 |
0100 |
4 |
0100 |
5 |
0101 |
5 |
0101 |
6 |
0110 |
6 |
0110 |
7 |
0111 |
7 |
0111 |
8 |
1000 |
8 |
1000 |
9 |
1001 |
9 |
1001 |
10 |
1010 |
A |
0001 0000 |
11 |
1011 |
B |
0001 0001 |
12 |
1100 |
C |
0001 0010 |
13 |
1101 |
D |
0001 0011 |
14 |
1110 |
E |
0001 0100 |
15 |
1111 |
F |
0001 0101 |
16 |
10000 |
10 |
0001 0110 |
17 |
10001 |
11 |
0001 0111 |
1.1.2 Перевод чисел из одной позиционной системы счисления в другую
Существует два основных метода перевода чисел из одной СС в другую:
табличный и расчетный.
Табличный метод основан на составлении специальных таблиц соответствия чисел в различных СС, примером такой таблицы является таблица 1.1. Такие таблицы удобны на начальном этапе ознакомления с новой СС, но являются громоздкими.
6

Расчетный метод более универсален, но применим только к позиционным СС. При использовании расчетного метода могут встретиться три случая: перевод целых чисел, перевод правильных дробей, перевод неправильных дробей.
Правило перевода целых чисел из одной позиционной СС в другую. Ис-
ходное целое число необходимо последовательно делить на основание новой СС до тех пор, пока не получится частное, у которого целая часть равна нулю. Деление необходимо производить в исходной СС. Результат перевода записывается из остатков от последовательного деления, причем последний остаток будет старшим разрядом (СР) числа в новой СС.
Процесс деления сначала самого числа, а затем целых частей получаемых частных на один и тот же делитель называется последовательным делени-
ем.
Пример 1.1. Преобразуем десятичное число X = 29 в двоичную и шестнадцатеричную СС:
|
29 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
29 |
16 |
|
|
|
||||||||||
28 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
14 |
2 |
|
|
|
|
|
|
|
|
16 |
1 |
16 |
|||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
||||
14 |
7 2 |
|
|
|
|
|
|
D 13 |
0 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
CP |
|||||
|
|
|
6 |
|
|
3 |
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
2 |
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
CP |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Стрелкой показан порядок записи числа в новой СС.
Ответ: X = 29(10) = 11101(2) = 1D(16).
Правило перевода правильных дробей из одной позиционной СС в дру-
гую. Исходную правильную дробь необходимо последовательно умножать на основание новой СС до тех пор, пока в новой дроби не будет нужного количества цифр, которое определяется требуемой точностью перевода. Результат перевода записывается из целых частей произведений, получающихся при последовательном умножении, причем первая целая часть будет старшим разрядом результата. Умножение выполняется в исходной СС.
Процесс умножения сначала самой исходной дроби, а затем дробных частей получаемых произведений на один и тот же множитель называется по-
следовательным умножением.
7

Пример 1.2. Переведем в двоичную и шестнадцатеричную СС правильную дробь X = 0.325(10) с точностью четыре знака после точки:
x |
0 .3 2 5 |
x |
0. 3 2 5 |
|
2 |
|
1 6 |
CP – |
0. 6 5 0 |
CP – |
5 .2 0 0 |
x |
x |
||
|
2 |
|
1 6 |
|
|
|
|
x |
1. 3 0 0 |
x |
3. 2 0 0 |
|
2 |
|
16 |
|
0. 6 0 0 |
|
|
x |
x |
3. 2 0 0 |
|
|
2 |
|
16 |
|
1. 2 0 0 |
|
|
|
|
3. 2 0 0 |
Стрелкой показан порядок записи правильной дроби в новой СС.
Ответ: X = 0.325(10) = 0.0101(2) = 0.5333(16).
Заметим, что в случае если дробная часть на некотором шаге становится равной нулю, то процесс преобразования на этом заканчивается.
При переводе неправильных дробей отдельно преобразуют целую и дроб-
ную части по соответствующим правилам, приведенным выше, а затем записывают результаты перевода через точку в новой СС.
Пример 1.3. Преобразуем неправильную дробь X = 29.325(10) в двоичную и шестнадцатеричную СС с точностью четыре знака после точки:
X = 29.325(10) = 11101.0101(2) = 1D.5333(16).
Рассмотренный расчетный метод удобен в том случае, если исходной является десятичная СС. Если же перевод осуществляется из недесятичной СС, то вычисления затруднительны. В этом случае для преобразования чисел можно использовать формулу (1.1), причем расчеты ведутся в новой СС.
Пример 1.4. Преобразуем в десятичную СС двоичное число X = 11101.0101: X = 11101.0101(2) = 1 ∙ 24 + 1 ∙ 23 + 1 ∙ 22 + 0 ∙ 21 + 1 ∙ 20 + 0 ∙ 2-1 + 1 ∙ 2-2 + 0 ∙ 2-3+
+1 ∙ 2-4 = 16 + 8 + 4+ 0 + 1 + 0 + 0,25 + 0 + 0,0625 = 29.3125(10) ≈ 29.325(10).
Из примера 1.4 следует, что целая часть числа переводится точно, а дробнаяприближенно.
Таким образом, для перевода десятичных чисел в другую позиционную СС используется метод последовательного деления-умножения, а при обратном переводе исходное число записывается в виде полинома по формуле (1.1) и выполняются необходимые расчеты.
8
1.1.3 Формы представления чисел в цифровых устройствах
Числа в цифровых устройствах могут представляться в форме целых чисел,
чисел с фиксированной точкой (в естественной форме) и чисел с плавающей точкой (в нормальной форме).
Целые числа. При решении задач целые числа встречаются в случаях представления индексов переменных, подсчета числа повторений каких-либо действий и т. д. Для хранения целых чисел в памяти предусматривается разрядная сетка, состоящая из определенного количества двоичных разрядов. Один из n разрядов отводится под знак числа, остальные разряды отводятся под модуль числа. Для положительных чисел в знаковом разряде записывается цифра 0, а для отрицательных – цифра 1.
Модуль числа занимает в разрядной сетке ее младшие разряды, свободные старшие разряды заполняются нулями. Если количество значащих разрядов модуля числа превышает n-1, происходит потеря старших разрядов модуля. Это явление, называемое переполнением разрядной сетки, приводит к ошибке в представлении числа.
Диапазон модулей чисел, которые могут быть представлены в n-разрядной сетке, от 0 (при цифре 0 во всех разрядах модуля) до 2n-1 (при цифре 1 во всех разрядах модуля). Например, при n = 16 максимальное значение модуля числа будет равно:
215-1 = 25 ∙ 210-1 = 32 ∙ 1024-1 ≈ 32 ∙ 103.
Числа с фиксированной точкой. Естественной называется такая форма числа, которая в неявном виде реализует формулу (1.1), т. е. число записывается только с помощью набора значащих цифр без явного указания их весов и знаков сложения. Отсчет разрядов ведется от точки (что равносильно указанию их весов), которая обычно фиксируется между целой и дробной частями числа. При этой форме обычно точка, отделяющая целую часть числа от ее дробной части, фиксируется перед старшим разрядом модуля числа (рисунок 1.1).
9

|
Знак
числа
2 |
1 |
2 |
2 |
2 |
3 |
|
|
2 |
m |
|||
|
|
|
|
|
|
|||||||
a 1 |
|
a 2 |
|
a 3 |
|
… |
|
a m |
||||
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||||
|
||||||||||||
Разряды модуля числа
Положение точки
Рисунок 1.1 – Распределение разрядной сетки для двоичных чисел с фиксированной точкой
Таким образом, значение модуля числа всегда оказывается меньше единицы. Это условие путем выбора определенных масштабных коэффициентов должно выполняться для исходных данных задачи и всех промежуточных результатов вычислений.
При записи числа в ячейку памяти свободные младшие разряды заполняются нулями, а если число разрядов модуля больше n-1, то младшие разряды модуля, которые не поместились в разрядной сетке, теряются. Это приводит к погрешности, значение которой меньше единицы младшего разряда разрядной сетки.
Если число имеет целую часть, то для ее хранения в разрядной сетке места нет, она теряется, число в разрядной сетке оказывается ошибочным.
Диапазон чисел одного знака, представляемых в цифровом устройстве с фиксированной точкой будет равен:
|
|
|
|
|
|
|
|
|
|
| | |
|
|
(1.2) |
||
Числа меньше |
2 |
m |
представляются как машинный нуль, а числа больше |
||||||||||||
|
|||||||||||||||
|
|
|
|||||||||||||
1 2 |
m |
приводят к переполнению разрядной сетки. Область представляемых |
|||||||||||||
|
|
||||||||||||||
|
|
|
|||||||||||||
чисел показана на рисунке 1.2. |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
Предста- |
|
Область |
|
Предста- |
|||||
|
|
Переполнение |
|
|
вимые |
|
|
вимые Переполнение |
|||||||
|
|
|
|
машинного нуля |
|
||||||||||
|
|
|
|
|
|
числа |
|
|
числа |
||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Истинный нуль |
|
|
|
Числовая ось |
|
|
|
|
Aмакс |
Aмин |
|
Aмин |
Aмакс |
||||||||
Рисунок 1.2 – Область представляемых чисел с фиксированной точкой
10
