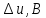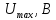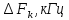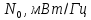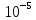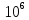Среднее Заочное отделение / 2 семестр 2016 / ТЭС 1

Задание 1

1.1 Составьте определения терминов, приведённых в таблице 1. Приведите временные диаграммы сигналов и поясните их особенности.

Таблица 1 – Исходные данные

номер варианта	наименование термина
6	гармонический сигнал

1.2 Нарисуйте временную диаграмму периодической последовательности прямоугольных импульсов (ПППИ) с заданными в таблице 2 параметрами. Рассчитайте и постройте спектры амплитуд и фаз этого сигнала. Поясните, от каких факторов зависит спектральный состав периодического сигнала прямоугольной формы и рассчитайте ширину его спектра..

Таблица 2 – Исходные данные

номер варианта	период следования импульсов Т,мкс	длительность импульса τ u ,мкс	амплитуда импульса U m,,В
6	40	10	3

Решение:

1. Непрерывный сигнал – сигнал, мгновенные значения которого изменяются во времени плавно, без резких скачков (разрывов). Многие реальные сигналы являются непрерывными (электрические сигналы при передачи речи, музыки, многих изображений и т.д.) Приведем примеры временных диаграмм непрерывных сигналов.

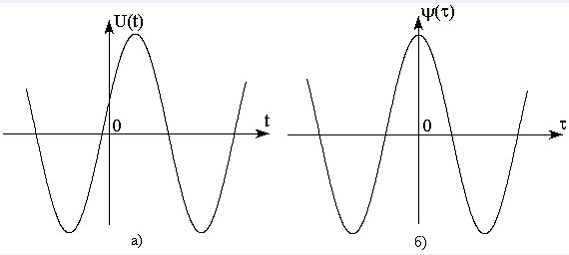
Рисунок 1 – Диаграммы непрерывных сигналов

1.2 При построении спектра ПППИ необходимы следующие параметры:

1) скважность;

2) частота первой гармоники спектра;

3) амплитуда постоянной составляющей;

4) амплитуды гармонических составляющих спектра. Рассчитаем данные параметры.

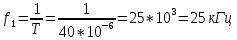
Определим частоту первой гармоники спектра

Определим скважность сигнала

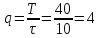
Определим амплитуду постоянной составляющей

Амплитуды гармонических составляющих рассчитываются по формуле

где k – порядковый номер гармоники.

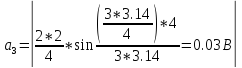
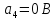
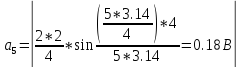
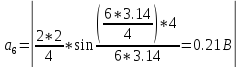
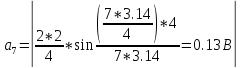
Изобразим временную диаграмму ПППИ.

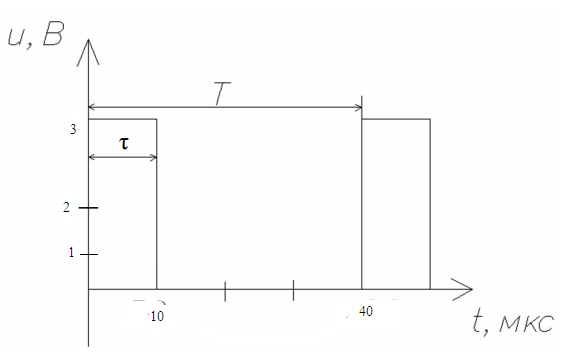
Рисунок 2 - Временная диаграмма ПППИ

Построим спектр амплитуд и фаз данного сигнала

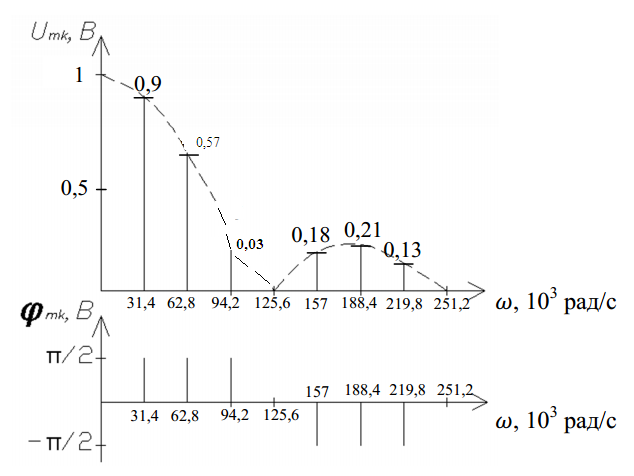
Рисунок 3 - Спектральная диаграмма ПППИ

Определим ширину спектра ПППИ по формуле

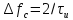
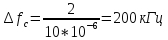
Ответ:

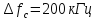
Задача 2

2.1 На рисунке 4 показана реализация напряжения первичного сигнала u(t) в системе передачи речи с максимальной частотой спектра Fмакс. С какой частотой при этом работает генератор стробирования (взятия отсчетов) речевого сигнала, если шаг дискретизации во времени ∆t = 2/1 Fмакс ? Каким числом реализаций определяется речевой сигнал на интервале времени T при дискретизации во времени и квантовании по уровню с шагом ∆u и максимальным значением напряжения сигнала U макс

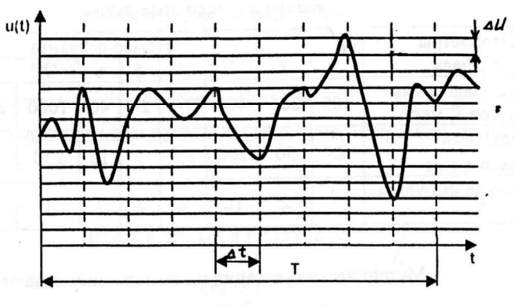
Рисунок 4 – Реализация напряжения первичного сигнала

Таблица 3 – Исходные данные

номер варианта		Т,мс
6	9	10	0,02	4

Решение:

Определим шаг дискретизации по времени по формуле

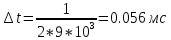
Определим частоту генератора стробирования по формуле

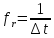
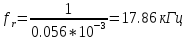
Определим число передаваемых отсчетов ( k ) на интервале времени Т по формуле

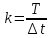
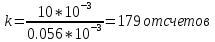
Определим число разрешенных уровней квантования по формуле

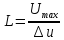
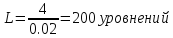
Определим число реализаций, которым определяется речевой сигнал на интервале времени 4мс при дискретизации во времени и квантовании по уровню с шагом 0,02 В и максимальным значением напряжения сигнала 2В, по формуле

Ответ:

Задача 3

3.1 Составьте определения терминов, приведённых в таблице 4. Поясните их особенности.

Таблица 4 – Исходные данные

номер варианта	наименование термина
6	Тепловой шум,канал тотальной частоты

3.2 Канал связи с полосой ∆Fк предполагается использовать в течение времени ∆Тк. (таблица 5). Известно, что в канале связи действует шум с равномерной спектральной плотностью N0. Определите предельную мощность сигнала Рмакс, который может быть передан по данному каналу с ёмкостью VK .

Таблица 5 – Исходные данные

номер варианта
6	5			30

Решение:

3.1 Приведем определения терминов

1.Канал тотальной частоты – это совокупность технических средств и среды распространения, обеспечивающая передачу электрических сигналов, связи в эффективно передаваемой полосе частот.

2. Тепловой шум – равновесный шум обусловленный тепловым движением носителей зарядов, в проводнике, в результате чего на концах проводника возникает флуктуирующая разность потенциалов.

3.2 Динамический диапазон сигнала определяется по формуле

Dc = 10 lg(Pмакс / Pш ),

где Рш – мощность шума в канале.

Р ш определяется следующим образом:

Pш = N0 *∆Fк

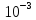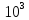Pш=**5*=5*

С другой стороны Dc определяется как:

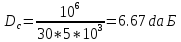
Выразим Pmax из следующим образом

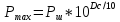
Ответ:

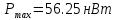
Задача 4

4.1 Поясните свойства нелинейных элементов и необходимость аппроксимации ВАХ нелинейных элементов.

4.2 На вход нелинейного элемента, вольтамперная характеристика которого аппроксимирована полиномом второй степени i=a0+a1u+a2u2, мА, подаётся сумма двух гармонических колебаний u=Uω sinωt+UΩ sinΩt. Согласно исходным данным, приведённым в таблице 6, рассчитайте спектральный состав отклика нелинейного элемента, постройте в масштабе спектральную диаграмму тока на выходе нелинейного элемента.

Таблица 6 – Исходные данные

Вариант	Аппроксимирующая функция, мА	Входное воздействие, В
6	i = 1,8 + 2u + 0,15	u = 2sin 2π ⋅ 800 t + sin 2π ⋅ 200 t

Решение:

4.1 Для любого нелинейного элемента (НЭ) характерна нелинейная зависимость между некоторыми его параметрами (между напряжением и емкостью, напряжением и током). Характеристики нелинейных элементов задают графиками, таблицами или приближенными аналитическими выражениями. Важнейшей особенностью любой нелинейной цепи является то, что для неё несправедлив принцип суперпозиции. Для получения количественных результатов при расчетах или анализе нелинейных цепей графического описания НЭ недостаточно. Необходимо также уметь описывать их математически. Замена заданной нелинейной характеристики аналитической функцией, приближенно выражающей заданную зависимость, называется аппроксимацией нелинейной характеристики. Примером нелинейной емкости может служить любое устройство с нелинейной вольткулонной характеристикой q(U). Примером нелинейной индуктивности L(I) служит катушка с ферромагнитным сердечником, обтекаемая сильным током, доводящим сердечник до магнитного насыщения. Еще одним свойством НЭ является нелинейность вольтамперной характеристики, т.е. отсутствует пропорциональность между током и напряжением.

4.2

i = 1,8 + 2u + 0,15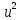 u = 2sin 2π ⋅ 800 t + sin 2π ⋅ 200 t

ω 1 = 2π ⋅10 4 рад/с; ω 2 = 2π ⋅10 3 рад/с.

Рассчитаем спектральный состав отклика нелинейного элемента

i = 1,8+2 ⋅ (2sin 2π ⋅800 t + sin 2π ⋅200 t) + 0,15⋅(2sin 2π ⋅800 t + sin 2π ⋅ 200 t)² = 1,8 + 4⋅sin 2π⋅800t + 2 ⋅

⋅2 sin² 2π ⋅200t + 0,3 ⋅ sin 2π ⋅800t +0,15⋅sin 2π ⋅800t⋅sin 2π ⋅200 t + 0,15⋅sin 2π ⋅200 t = 1,8 + 4⋅sin 2π ⋅800t+ 2 ⋅sin² 2π ⋅200t + 0,17 – 0,17⋅cos 4π ⋅800 t + 2⋅cos 2π ⋅(800 - 200)t – cos 2π ⋅(800+200)t + 0,3 – 0,3 ⋅ cos 4π ⋅200 t = 2,27+ 4⋅sin2π⋅800 t +2⋅sin 2π ⋅200 t – 0,17 ⋅ cos 4π ⋅800 t + 0,3 ⋅ cos 4π ⋅9 ⋅200 t – cos 2π ⋅11 ⋅200t – cos 4π ⋅200t.

Спектральная диаграмма тока на выходе НЭ представлена на рисунке 6.

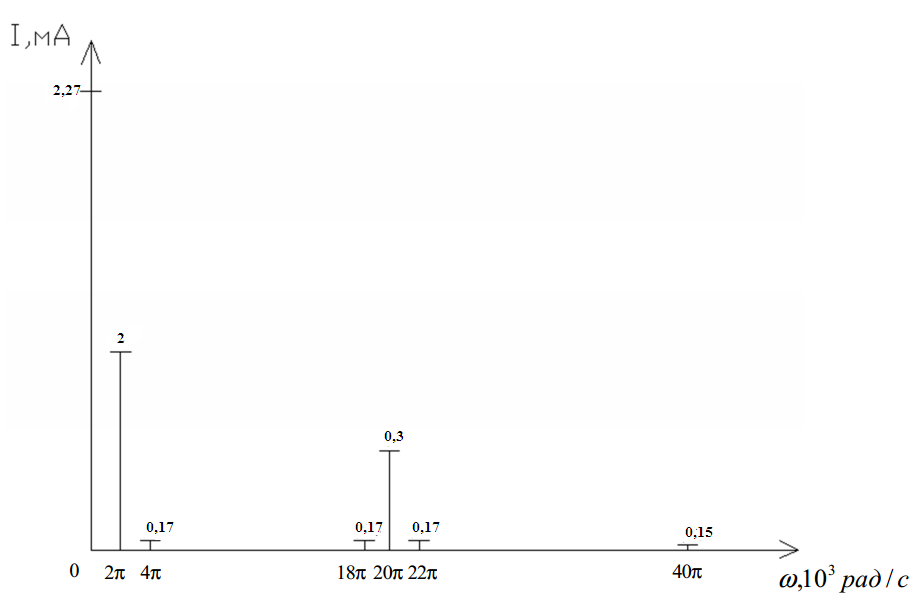
Рисунок 6 – Спектральная диаграмма тока на выходе НЭ

Задача 5

5.1 Составьте заданную в таблице 7 схему автогенератора. Поясните назначение элементов и режим самовозбуждения данного автогенератора.

Таблица 7 – Исходные данные

номер варианта	наименование термина
6	кварцевый LC автогенератор эквивалентный индуктивный трехточке

Решение:

5.1 Одним из генераторов, эквивалентным трехточечной индуктивной схеме, является кварцевый LC автогенератор эквивалентный индуктивный трехточке. Принципиальная электрическая схема этого генератора представлена на рисунке 7.

LC- генератор так называется, потому что в нем используется LC- контур.

Рисунок 7 - кварцевый LC автогенератор эквивалентный индуктивный трехточке

В момент включения питания в коллекторной цепи транзистора VT появляется коллекторный ток, заряжающий емкость контура. В следующий момент времени заряженный кондер разряжается на катушку индуктивности. В контуре возникают свободные затухающие колебания частотой.

Трехточечные схемы называются трехточечными, поскольку контур подключается к трем выводам транзистора.

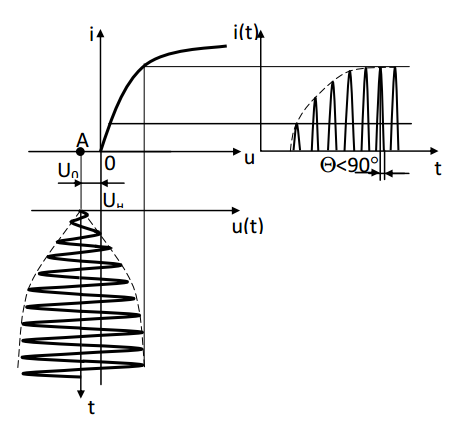
Рисунок 8 Диаграммы, поясняющие жесткий режим самовозбуждения

На практике в некоторых типах генераторов (в частности в LC-генераторах) используют оба режима: при включении генератора и во время переходного режима генератор работает в мягком режиме самовозбуждения, а при переходе в стационарный режим работы генератор переводится в жесткий режим самовозбуждения.