Явления переноса в газах Лекция 7 Средняя длина и среднее время свободного пробега молекул. Явления переноса в газах. Диффузия.

Столкновения между молекулами играют очень важную роль во всех процессах, происходящих в газах. В частности, столкновения устанавливают равновесное распределение (Максвелловское) молекул по скоростям. Столкновения это и есть тот механизм, обеспечивающий переход газа к равновесному состоянию.

В идеальном газе столкновения происходят только между двумя молекулами. На одновременные столкновения между тремя и большим числом молекул можно не обращать внимания, так как они происходят достаточно редко. Столкновения молекул - случайные события. Их число зависит от скорости молекул, их размеров и концентрации. При столкновении молекулы сближаются до некоторого минимального расстояния, которое условно считается равным сумме радиусов молекул, взаимодействующих между собой.

Молекулы в этом случае надо представлять как твердые, упругие шарики с радиусами r₁ и r₂. Если газ однородный, то r₁ = r₂ = r. Столкновение между молекулами происходят только в случае, если их центры сближаются на расстояние равное сумме их радиусов r = r = 2r (рис.1).

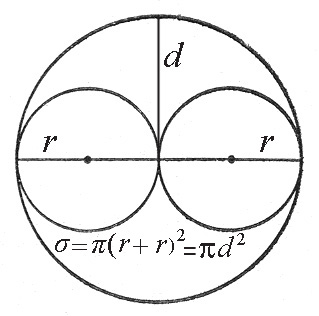
Рис.1. К расчету сечения рассеяния.

Иначе говоря, столкновение происходит только в том случае, если центры молекул окажутся внутри окружности площадью:

(1)

Величина σ называется эффективным сечением рассеяния молекул, или просто сечением рассеяния. Величина d, то есть минимальное расстояние между центрами молекул при столкновении, называется эффективным диаметром молекулы.

В момент столкновения изменяется величина и направление скорости молекулы, после чего она движется прямолинейно до следующего столкновения. Расстояние, которое молекула проходит между столкновениями – случайная величина.

Среднее расстояние, которое молекула проходит между двумя последовательными столкновениями называется средней длиной свободного пробега молекул.

Число столкновений молекулы в единицу времени, очевидно, также является случайным.

Ее среднее значение называется средним числом столкновений молекулы в единицу времени.

Эти две связанные между собой величины – являются главными характеристиками процесса столкновения газовых молекул.

Определим эти величины. Предположим, что все молекулы газа неподвижны, кроме одной. Из-за столкновений с неподвижными молекулами она будет двигаться по ломаной линии (рис.2).

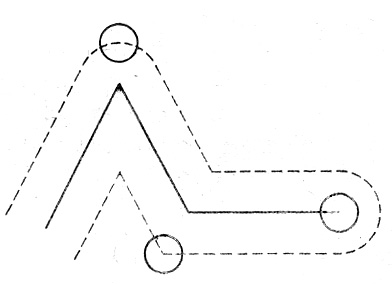
Рис.2. Траектория движения молекулы.

Пусть эффективный диаметр молекулы d. Она будет сталкиваться с теми неподвижными молекулами, центры которых находятся внутри цилиндра с площадью основания равной эффективному сечению рассеяния σ, т.е. окружности диаметром 2d (рис.3).

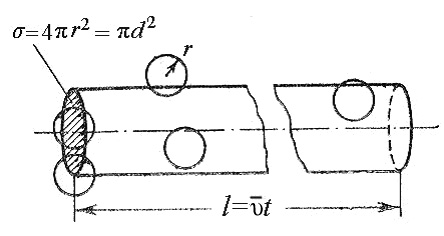
Рис.3. К расчету средней длины свободного пробега молекул.

Объем такого цилиндра равен пути, который молекула проходит за единицу времени, умноженному на σ:

где – средняя арифметическая скорость. Так как t = 1с то:

(2)

Ошибка, которая допускается при замене ломаного цилиндра на прямой незначительная, так как длина каждого прямого отрезка много больше, чем диаметр цилиндра.

Умножим объем цилиндра на концентрацию молекул n. В результате получим число молекул, находящихся в цилиндре, таким же будет и число столкновений рассматриваемой молекулы в единицу времени.

(3)

Однако следует учесть, что движется не одна, а все молекулы, поэтому число столкновений будет определяться не средней скоростью молекулы по отношению к стенкам сосуда (абсолютная скорость), а средней относительной скоростью (относительно движущихся молекул).

(4)

Пусть до столкновения молекулы движутся со скоростями υ₁ и υ₂ (рис.4).

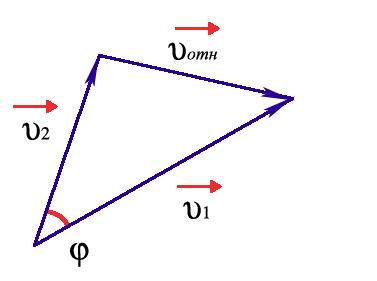
Рис. 4. К расчету относительной скорости.

Относительная скорость движения одной молекулы относительно другой:

Из рисунка видно, что:

Известно, что среднее значение суммы нескольких величин равно сумме средних значений этих величин.

Среднее значение квадратов абсолютных скоростей всех молекул одинаковое. Угол φ может принимать значения от 0 до π, поэтому среднее значение

Учитывая вышеизложенное, получим:

Средняя относительная скорость движения одной молекулы относительно другой в раз больше средней абсолютной скорости молекул. С учетом этого из (4) получим среднее число столкновений молекулы в единицу времени:

(5)

При нормальных условиях (p = 1,01·10⁵ Па, T = 273 K) значение из (5) составляет ~10⁹ с^-1.

Такое большое значение числа столкновений объясняет факт медленного движения молекул в определенном направлении, несмотря на то, что тепловые скорости молекул достигают сотен метров в секунду (пример: распространение запахов).

Величина обратная есть не что иное, как среднее время свободного пробега молекул:

(6)

За время t молекула проходит путь , за это же время молекула делает столкновений, следовательно, средняя длина свободного пробега молекул:

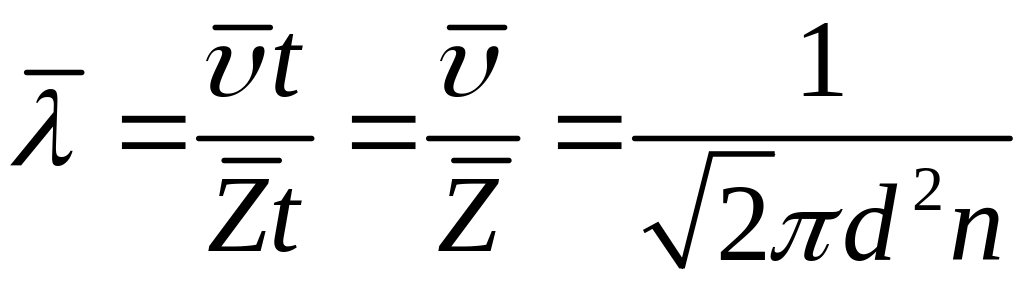(7)

При нормальных условиях .

Известно, что p = nkT. С учетом этого из (7) получим:

(8)

Из (8) видно, что обратно пропорциональна давлению при постоянной температуре. Из (7) следует, что не зависит от температуры. На самом деле эффективный диаметр молекулы d зависит (слабо) от температуры (от кинетической энергии сталкивающихся молекул). Зависимость выражается формулой Сезерленда:

(9)

где C – характерная для каждого газа постоянная величина, которая имеет размерность температуры и называется постоянной Сезерленда. - средняя длина свободного пробега молекулы при T→∞.

Равновесное состояние газа в МКТ всегда связано с хаотичным движением молекул, скорости которых распределены по Максвеллу. Любые неравновесные состояния газа связаны с нарушением Максвелловского распределения молекул по скоростям. Основная особенность неравновесного состояния – стремление газа самопроизвольно перейти к равновесному состоянию. Это обусловлено тепловым движением молекул и их беспрерывными столкновениями.

Установление в газе равновесного состояния с Максвелловским распределением по скоростям всегда связано с направленным переносом массы, импульса и энергии. Процессы переноса этих величин называются явлениями переноса. К явлениям переноса относятся: диффузия, внутреннее трение, теплопроводность. Диффузия обусловлена переносом массы, внутреннее трение – переносом импульса, теплопроводность – переносом энергии.

Диффузия. Диффузией называется процесс проникновения одного газа в объем другого, или движение газа из области с высокой концентрацией молекул в область, где она ниже.

Процесс диффузии заключается в том, что каждый из компонентов смеси переходит из тех мест, где его концентрация больше в те, где его концентрация меньше, это значит в направлении уменьшения концентрации.

Фик экспериментально установил, что масса вещества, переносимая через площадку dS в направлении нормали к площадке, за время dt, пропорциональна градиенту плотности в направлении переноса:

(10)

где dM – масса перенесенного вещества, - градиент плотности газа в направлении x, D – коэффициент диффузии, который зависит от рода газа и от условий, в которых газ находится.

Физический смысл D: коэффициент диффузии численно равен массе вещества перенесенной через единичную площадку в единицу времени, в направлении нормали к площадке, при единичном градиенте плотности.

(10) –закон Фика. Знак “-“ в правой части (10) показывает, что диффузионный поток направлен в сторону уменьшения плотности.

Рассмотрим самодиффузию газа (рис.4).

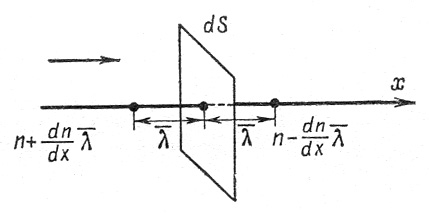
Рис.4. К расчету коэффициента диффузии.

Предположим, что концентрация молекул в том месте, где расположена площадка dS, равна n, а градиент концентрации молекул вдоль оси x – dn/dx. Тогда на расстоянии по обе стороны от площадки концентрации молекул будут соответственно равны:

(11)

(12)

Молекулы движутся хаотично, следовательно, все направления движения равновероятны. Тогда в направлении оси x будет двигаться 1/3 всех молекул. Из них половина, т.е. 1/6 будет двигаться слева направо, а вторая половина справа налево. Так как молекулы не сталкиваются друг с другом на пути , то за время dt через площадку dS слева на право пройдет

молекул, а в обратном направлении

молекул, где . Суммарное число молекул, которое проходит через площадку dS за время dt слева направо будет равно:

(13)

Суммарное число молекул, которое проходит через площадку dS за время dt справа налево подсчитывается аналогично:

(14)

Разность (14) и (13) даст общее число молекул, которые проходят через площадку dS за время dt в положительном направлении оси x:

(15)

С учетом (11) и (12) из (15) получим:

(16)

Умножим левую и правую часть (16) на массу одной молекулы m:

(17)

В (17) dNm = dM – масса газа, которая переносится через площадку dS за время dt, а величина:

градиент плотности, где mn = ρ – плотность газа. С учетом этого перепишем (17) в виде:

(18)

Сравнивая (18) с законом Фика (10) получим коэффициент диффузии:

(19)

В системе CI:

При T = const не зависит от давления p, а ~ 1/p, следовательно:

Коэффициент диффузии зависит от температуры, поскольку:

.

Следовательно . Опыты показывают, что при повышении температуры D возрастает быстрее, чем . Это объясняется тем, что при повышении температуры уменьшается эффективный диаметр молекул, что приводит к росту (формула Сезерленда), а, значит и к дополнительному увеличению D.