
- •Линейная алгебра
- •Место дисциплины в учебном плане
- •Цели и задачи курса
- •1. Матрицы. Основные понятия и определения. Действия над матрицами
- •Действия над матрицами
- •1. Сложение матриц
- •2. Умножение матрицы на число
- •3. Умножение матриц
- •1) Умножение матрицы-строки на матрицу-столбец
- •2) Умножение матриц
- •3) Умножение матрицы-столбца на матрицу-строку
- •Свойства определителей
- •Задачи для самостоятельной работы
- •3. Обратная матрица. Ранг матрицы
- •Правило вычисления ранга матрицы
- •Задачи для самостоятельной работы
- •4. Система линейных алгебраических уравнений
- •4.1. Метод Крамера и матричный способ решения системы линейных уравнений с неизвестными
- •4.2. Метод Гаусса решения системы линейных уравнений с неизвестными (метод последовательного исключения переменных)
- •Второй метод вычисления обратной матрицы.
- •Задачи для самостоятельной работы
- •Тренинг-тесты
- •Вопросы для самопроверки
- •Задачи для контрольных работ
- •Литература Основная
- •Дополнительная
- •Оглавление
Второй метод вычисления обратной матрицы.
Предположим, что матрица невырождена. Запишем матрицу в виде:
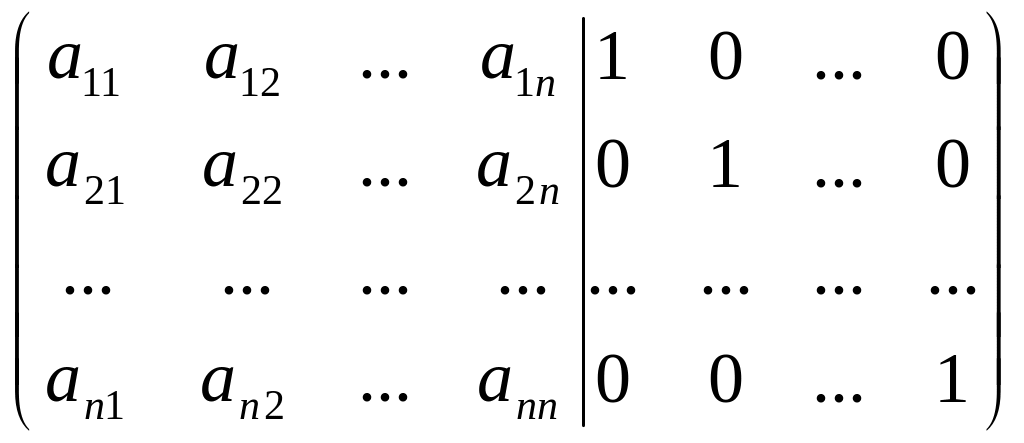 ,
,
т.е. присоединим к матрице единичную. Теперь с помощью элементарных преобразований (кроме перестановки строк местами) добьёмся того, чтобы построенная матрица приобрела вид:
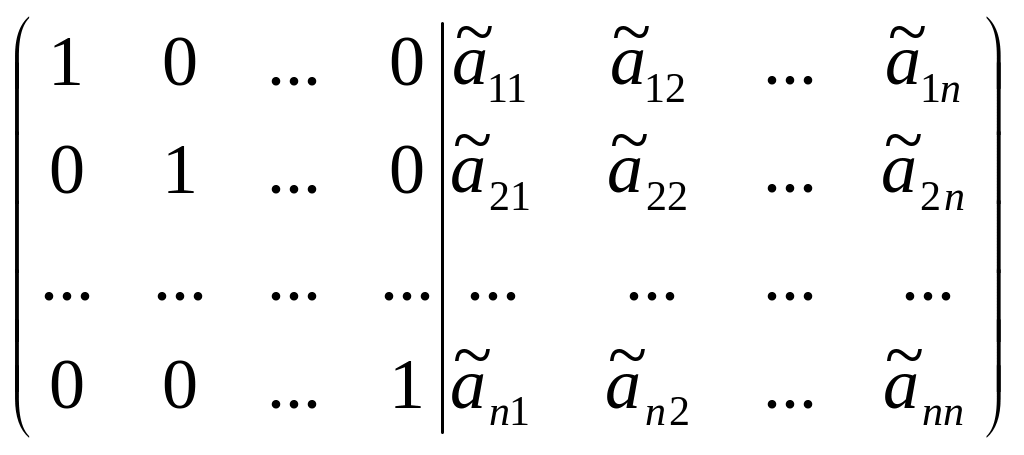
Тогда матрица
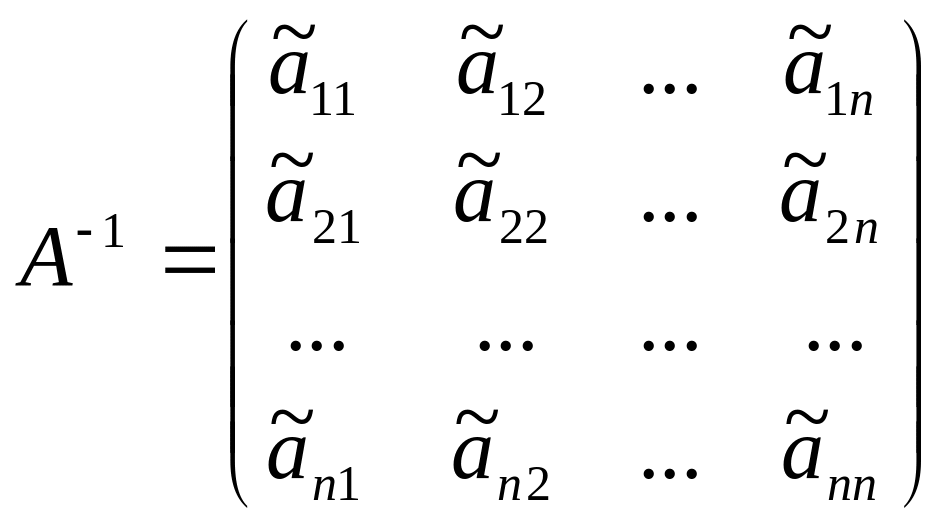
будет обратной для матрицы .
Пример
4.4. Вычислить
обратную матрицу для
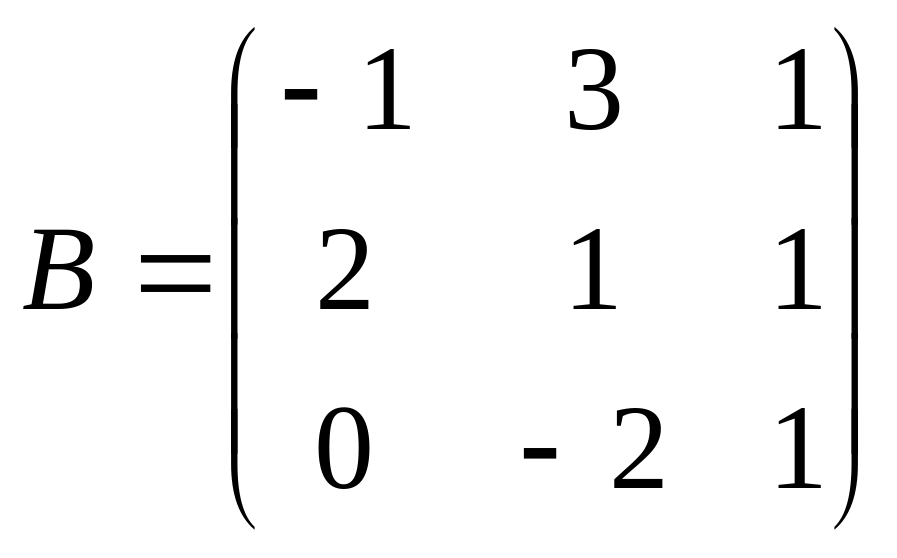
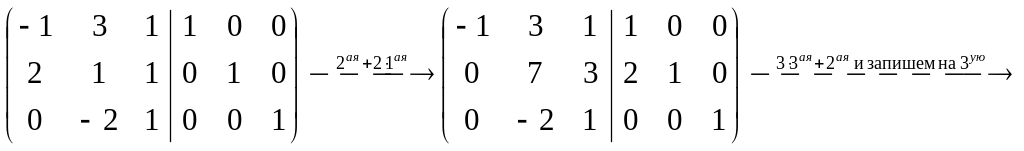
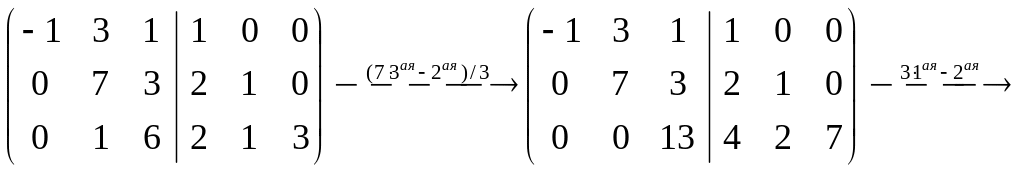
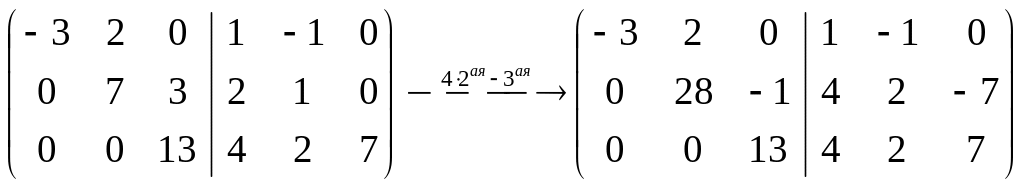
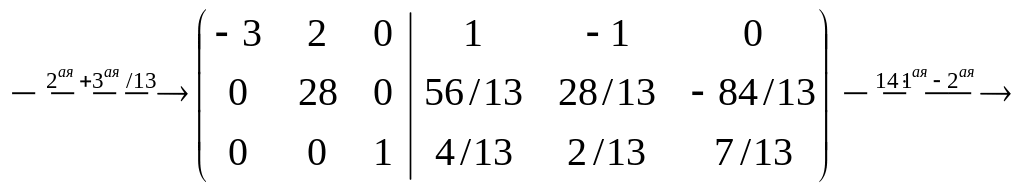
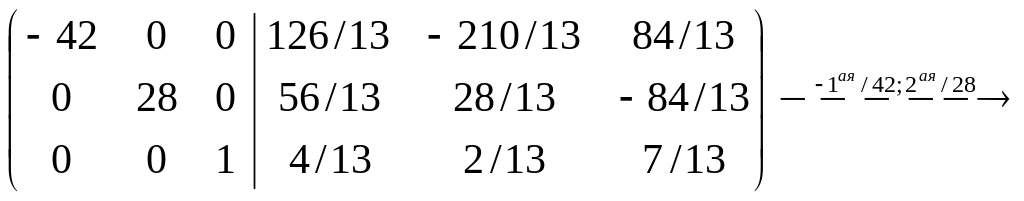
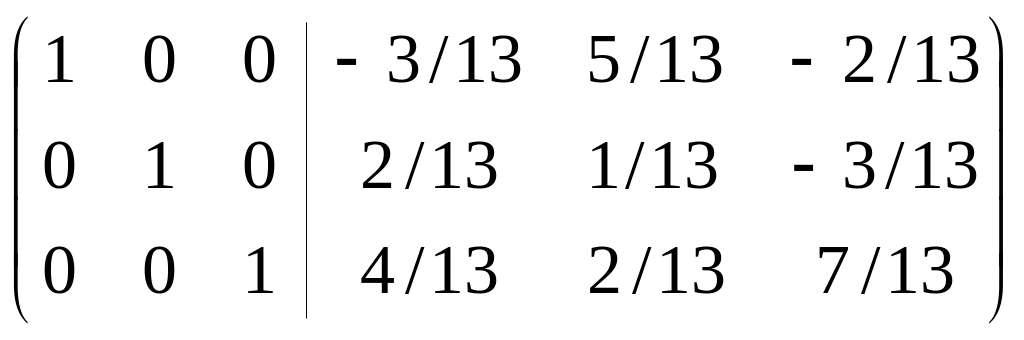 .
.
Следовательно,
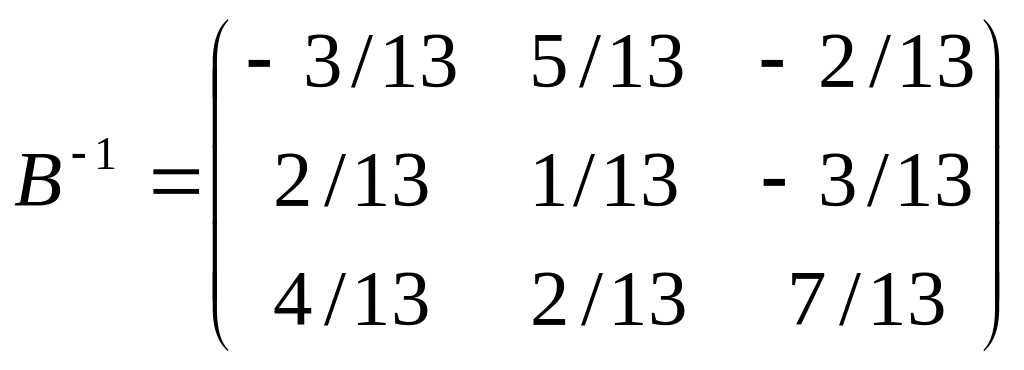
Задачи для самостоятельной работы
Решить системы уравнений методом Крамера, матричным методом, методом Гаусса.
1.
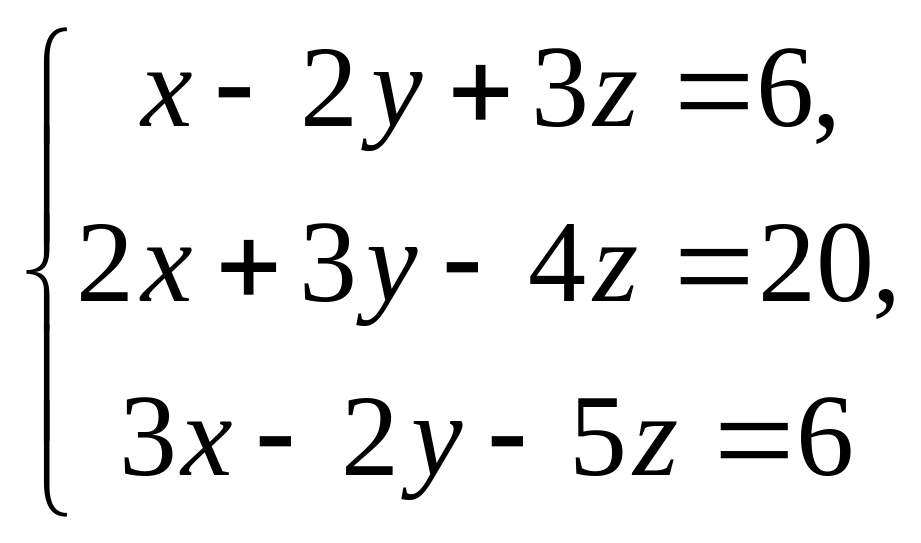 2.
2.
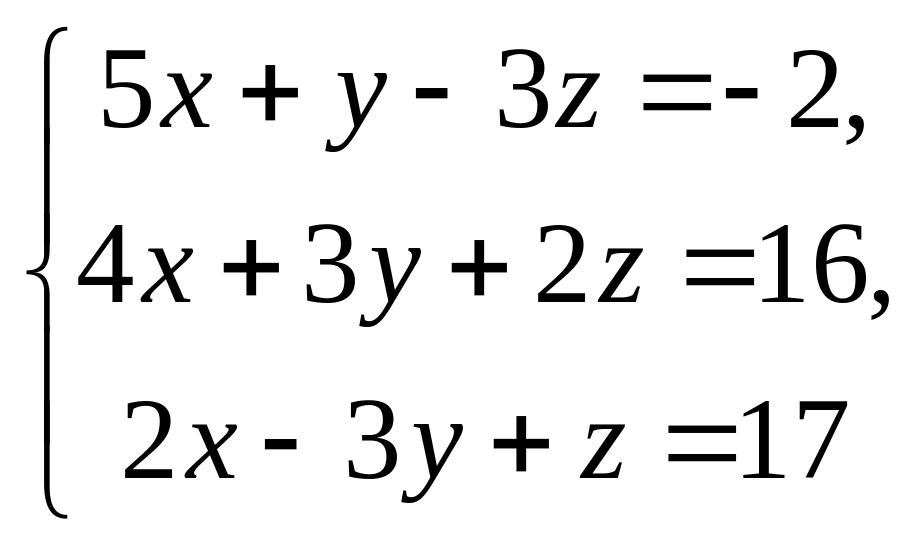
3.
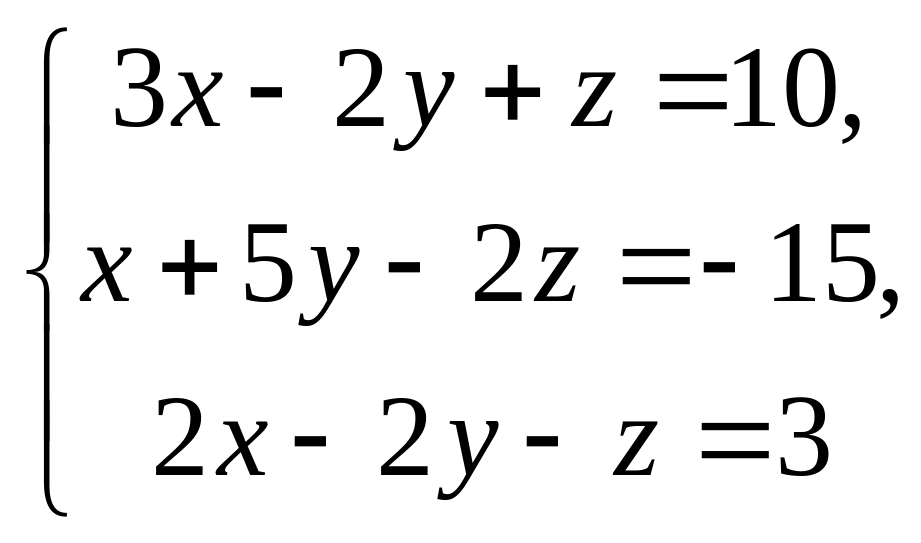 4.
4.

5.
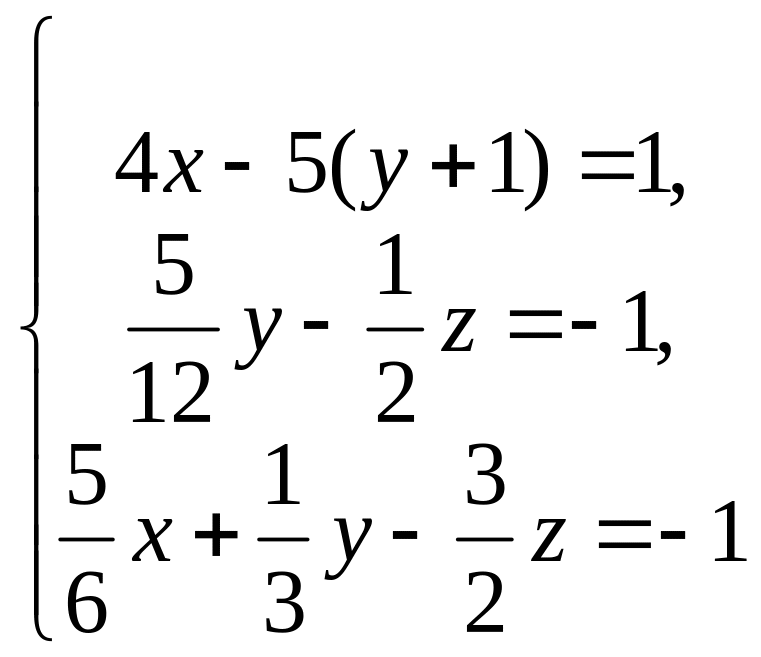 6.
6.
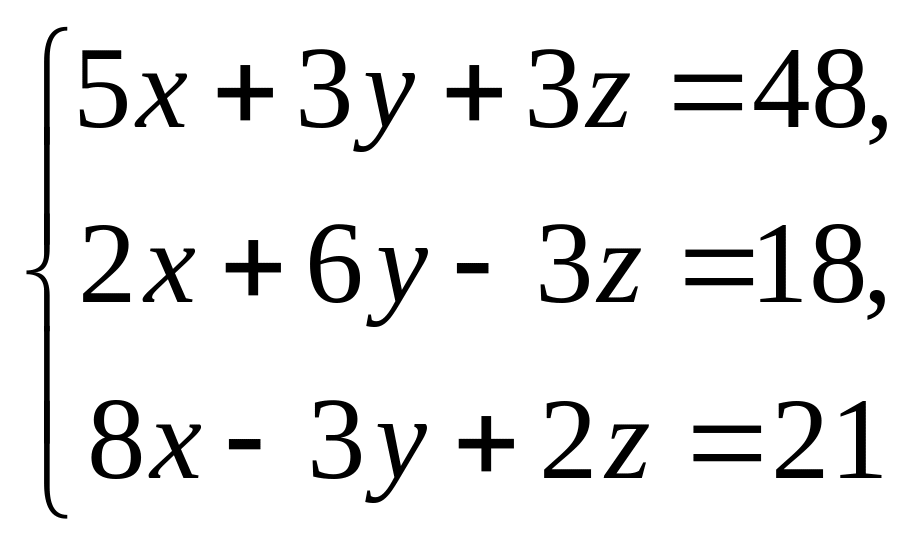
7.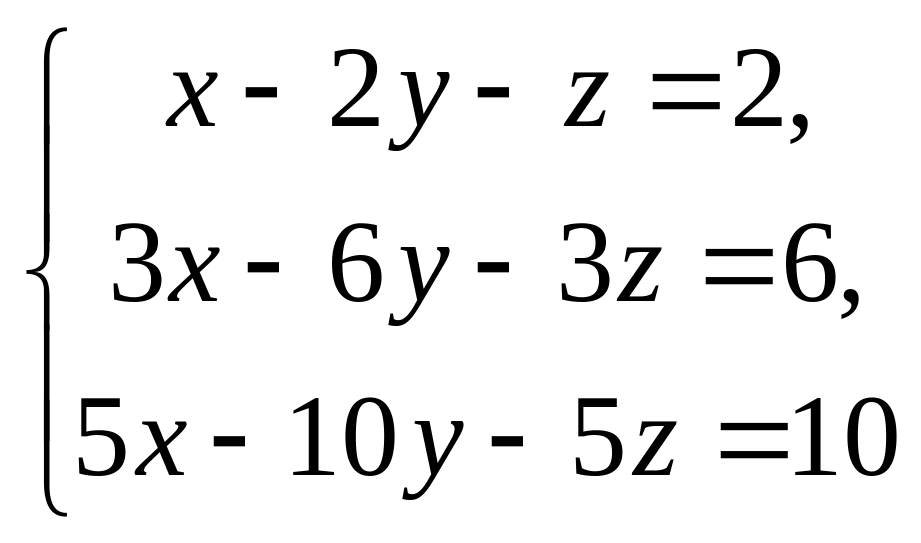 8.
8.
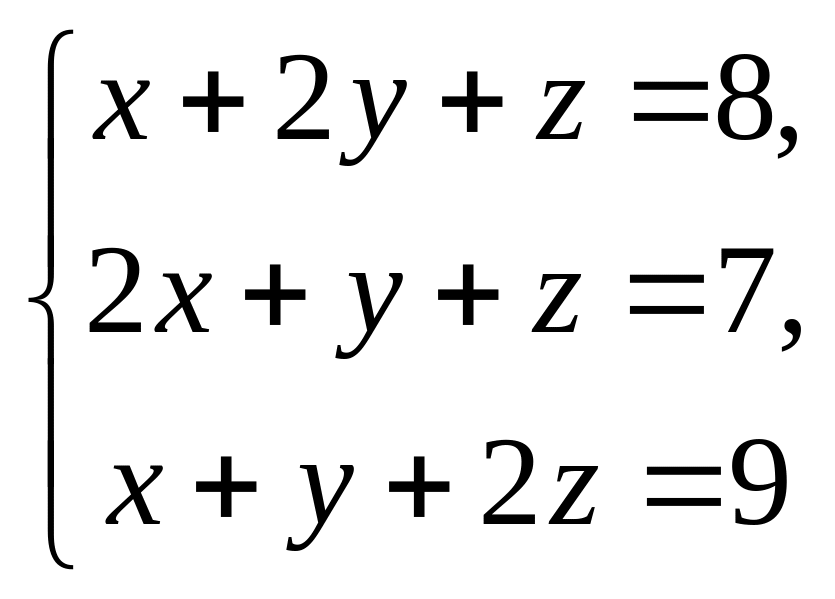
9.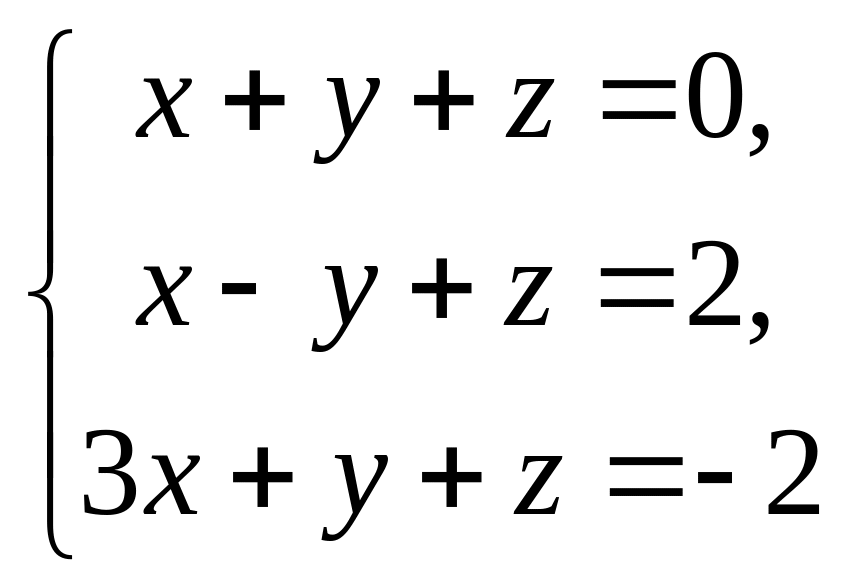 10.
10.
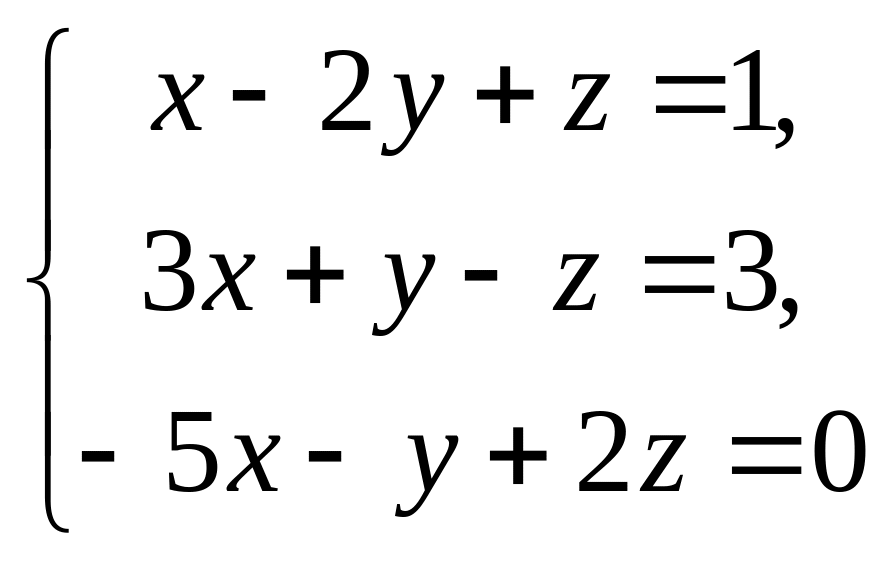
11.
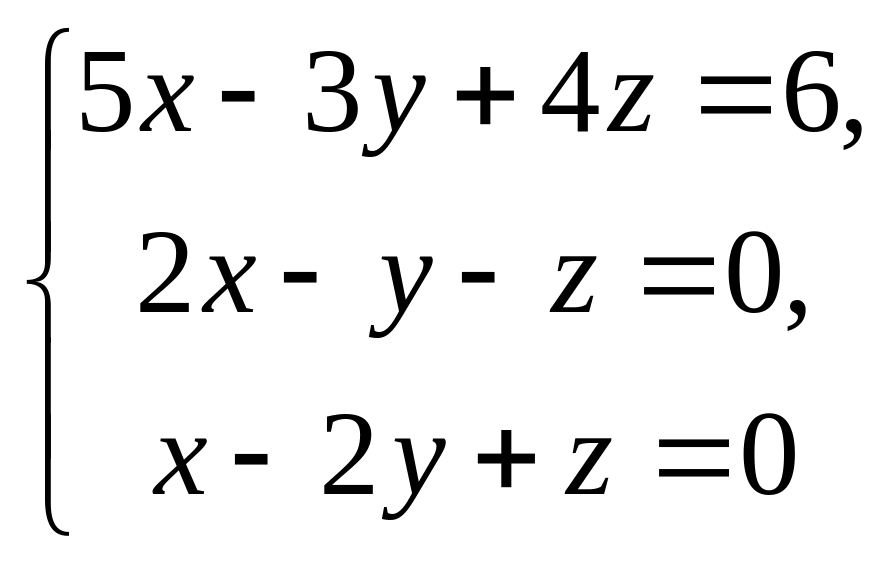
Тренинг-тесты
Выбрать один правильный ответ:
1.
Вычислить
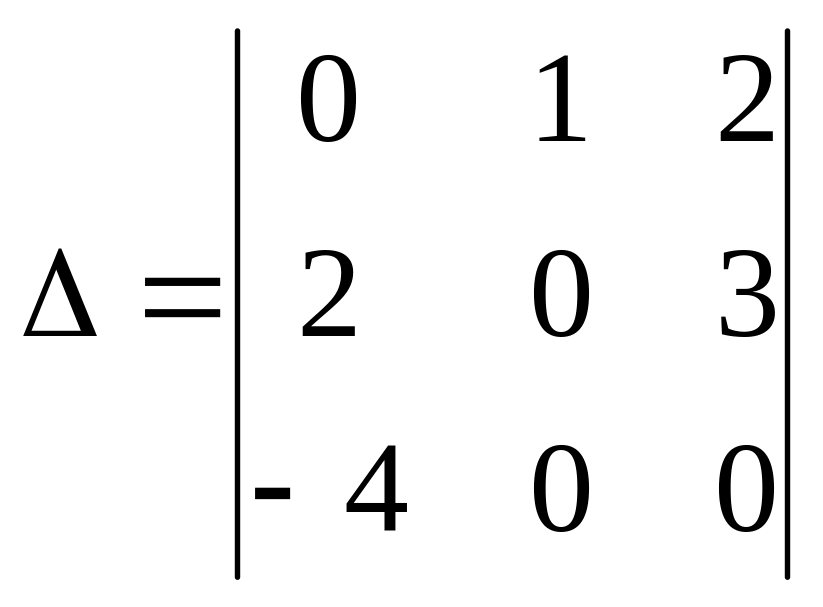
а) –8; б) 8; с) 1; д) 0.
2.
Вычислить
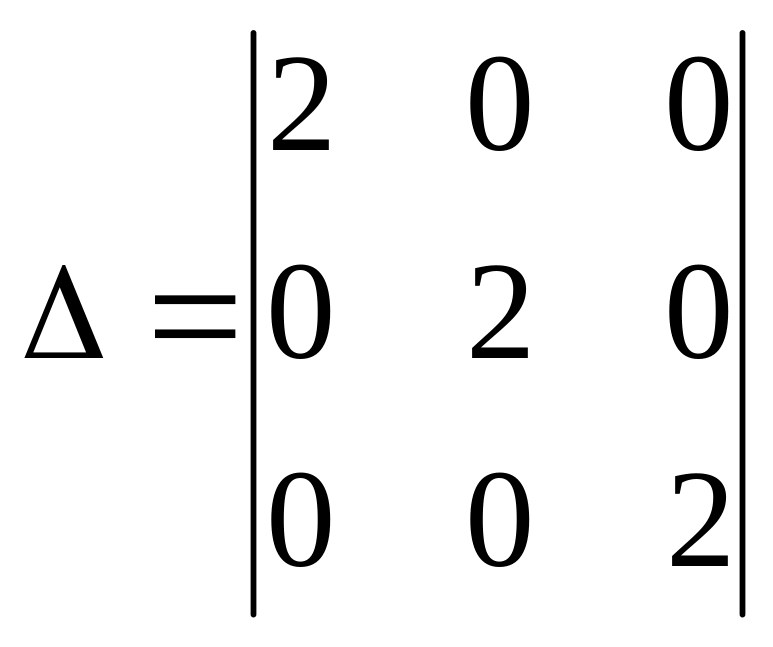
а) 8; б) –8; с) 0; д) 2.
3.
Вычислить
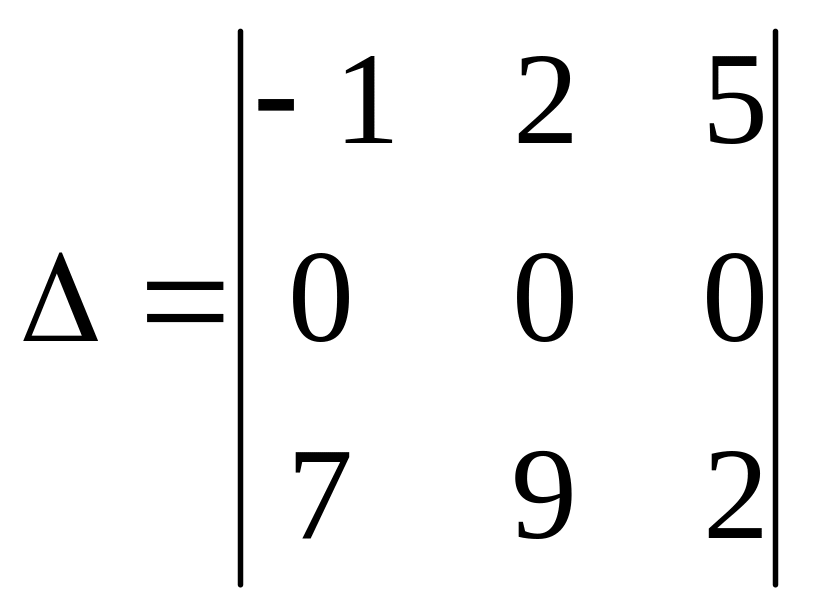
а) 0; б) –2; с) 2; д) 1.
4.
Вычислить
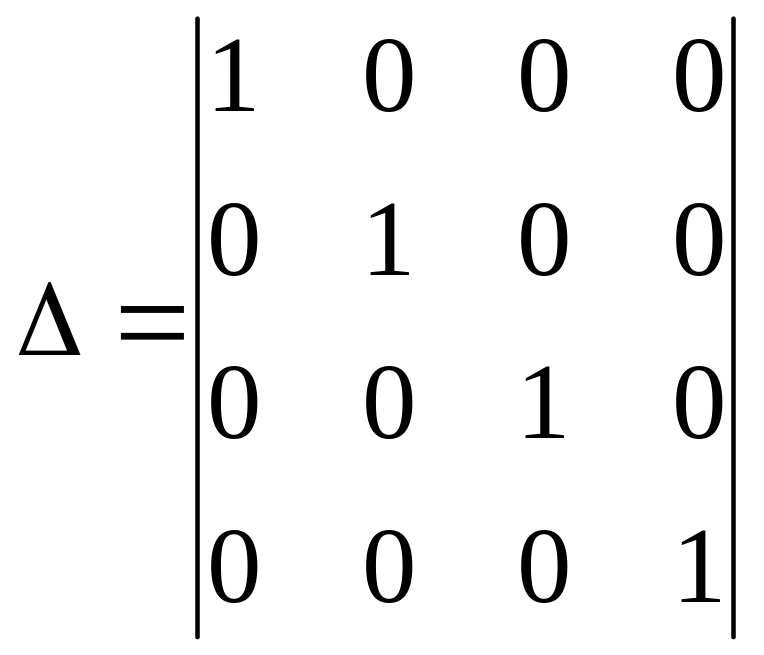
а) 1; б) –1; с) 0; д) 4.
5.
Вычислить
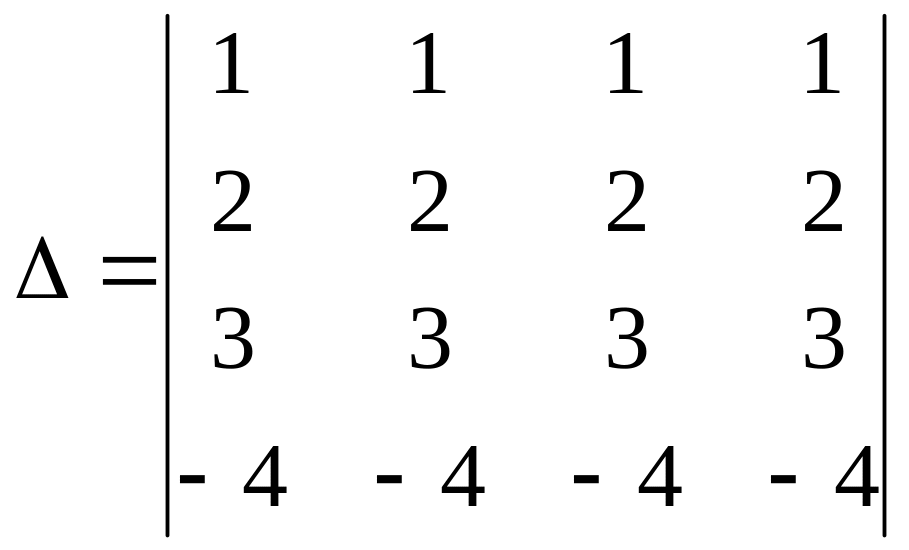
а) 0; б) –24; с) 3; д) –4
6.
Вычислить
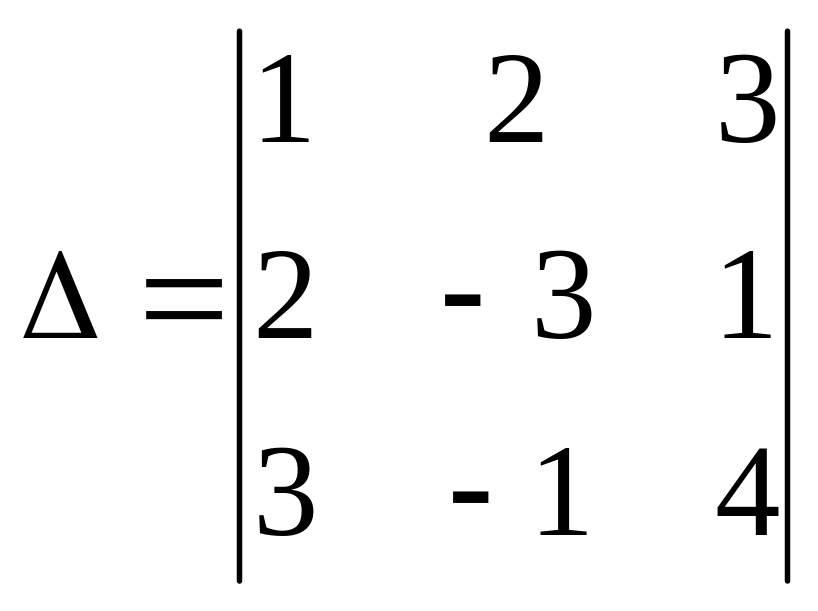
а) 0 ; б) 1; с) –1; д) –12.
7.
Вычислить
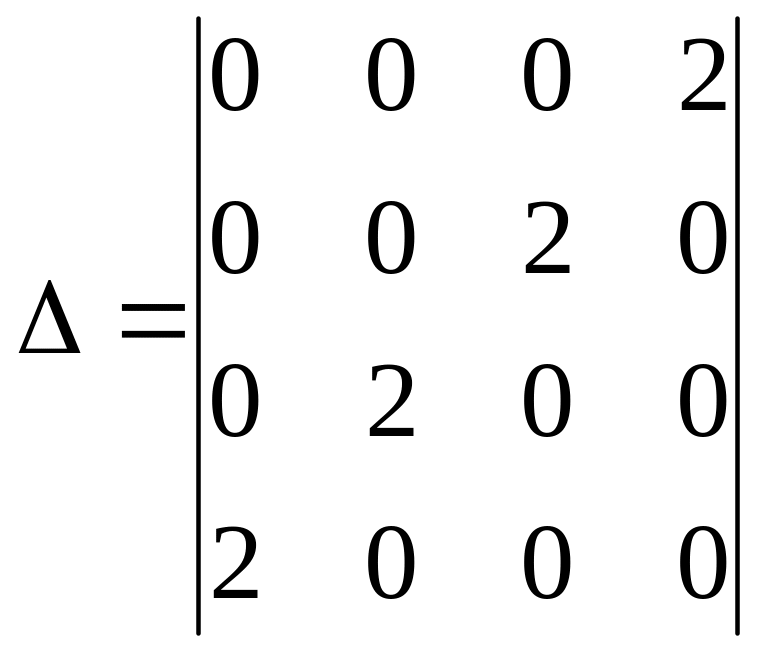
а) 16; б) –16; с) 0; д) 2.
8.
Вычислить
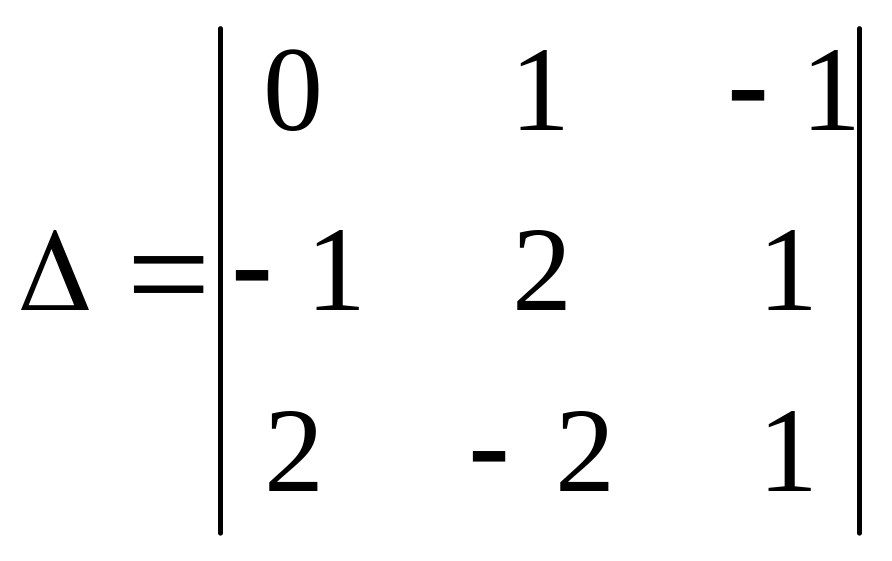
а) 5; б) –5; с) 3; д) 0.
9.
Найти
![]() ,
,
![]()
а)![]()
10.
Найти
![]()
![]()
Вопросы для самопроверки
Сформулируйте правила сложения матриц и умножение матрицы на число.
Каким законом подчиняются эти операции?
Как определяется операция умножения двух матриц?
Какие матрицы называются перестановочными?
Дайте определение транспонированной матрицы. Какую матрицу называют симметричной?
Какая матрица называется ступенчатой?
Что называется элементарными преобразованиями матрицы?
Что такое ранг матрицы и как его вычислить?
Какая система уравнений называется однородной? неоднородной?
Всегда ли совместна однородная система уравнений? А неоднородная?
Когда система уравнений имеет единственное решение?
Что такое общее решение системы уравнений?
Сформулируйте критерий разрешимости неоднородной системы уравнений?
Что называется определителем 2-го, 3-го и -го порядков?
Сформулируйте правило разложения определителя по строке (столбцу).
Что называется минором
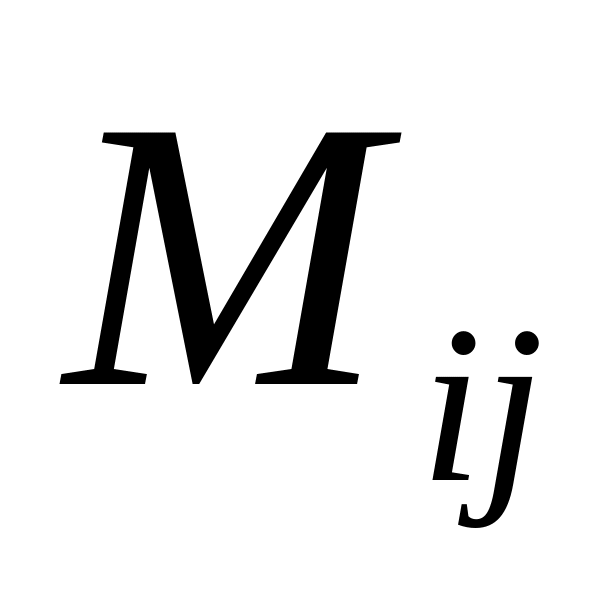 и алгебраическим дополнением
и алгебраическим дополнением
 элемента
элемента
 ?
?
Какая матрица называется не выровненной?
Дайте определение обратной матрицы. Какие вы знаете способы вычисления обратной матрицы?
Как записывается система уравнений в матрично-векториальной форме? Как найти решение системы уравнений при помощи обратной матрицы?
Сформулируйте, в чём состоит процедура Гаусса и для решения каких задач линейной алгебры она применяется?
Задачи для контрольных работ
Задание
1. Задана
система линейных алгебраических
уравнений
![]() ,
где
-
квадратная матрица размера
,
где
-
квадратная матрица размера
![]() с действительными элементами (матрица
коэффициентов),
–
матрица-столбец свободных членов.
Требуется найти решение этой системы
с действительными элементами (матрица
коэффициентов),
–
матрица-столбец свободных членов.
Требуется найти решение этой системы
![]() :
:
используя формулы Крамера,
с помощью обратной матрицы (матричный способ),
методом Гаусса.
Задание
2. Для матрицы
(матрица коэффициентов) найти
![]() .
.
1.
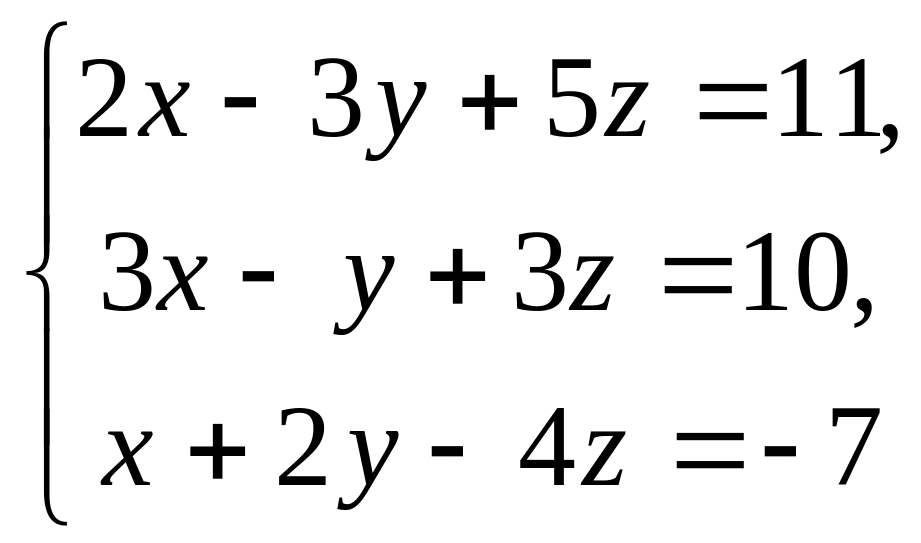 2.
2.
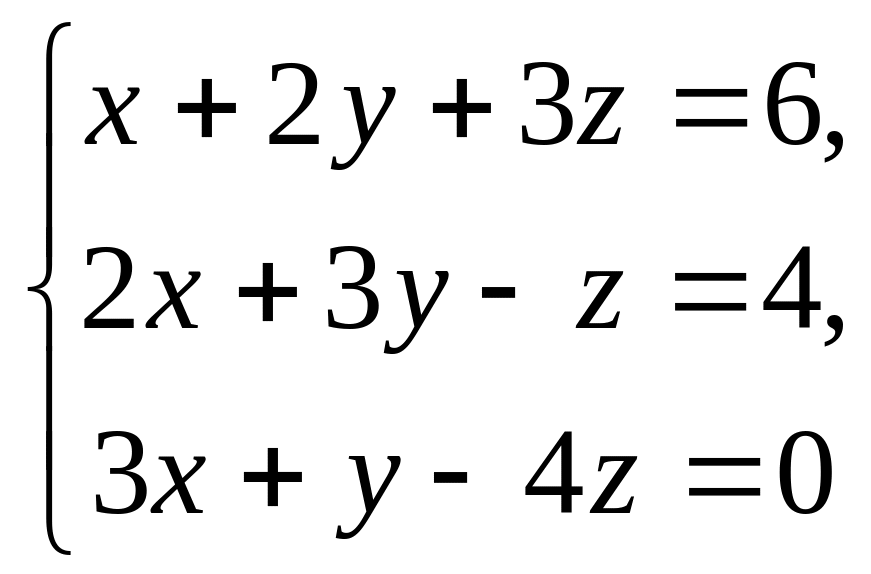 3.
3.
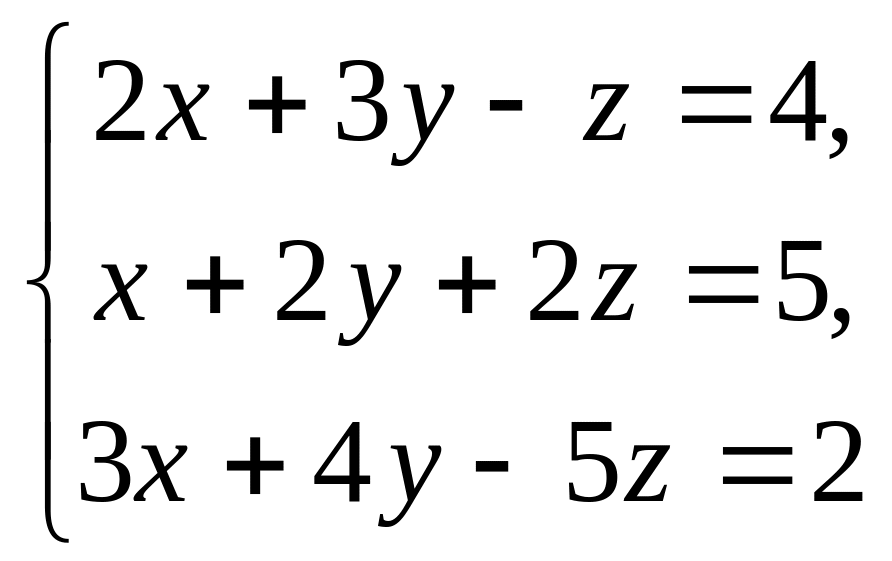
4.
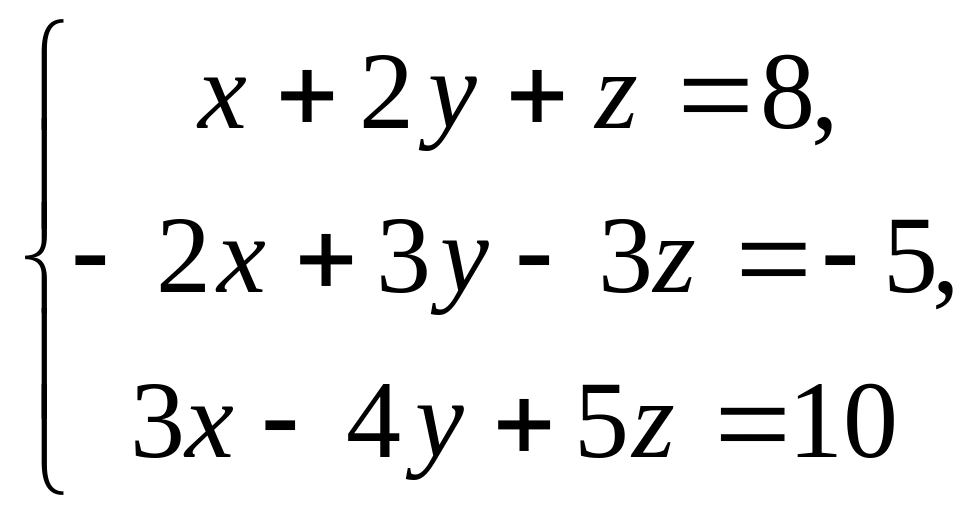 5.
5.
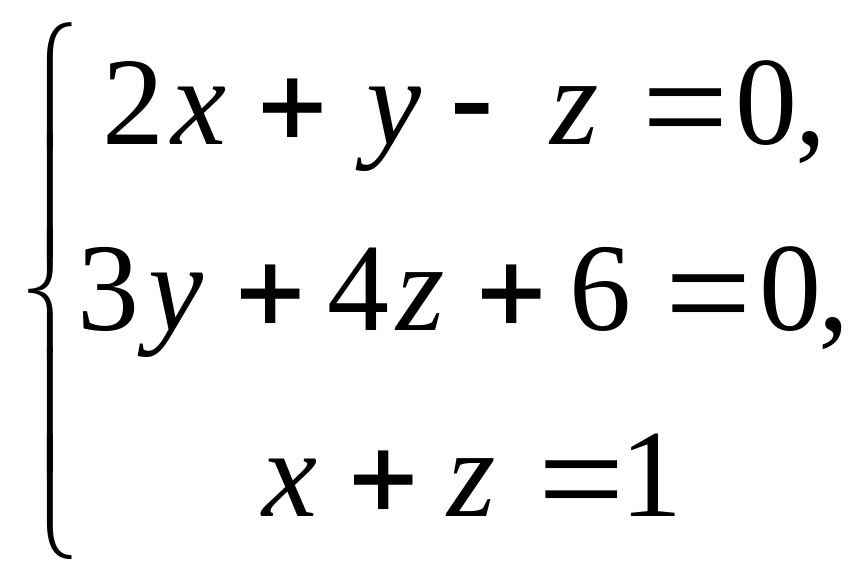 6.
6.
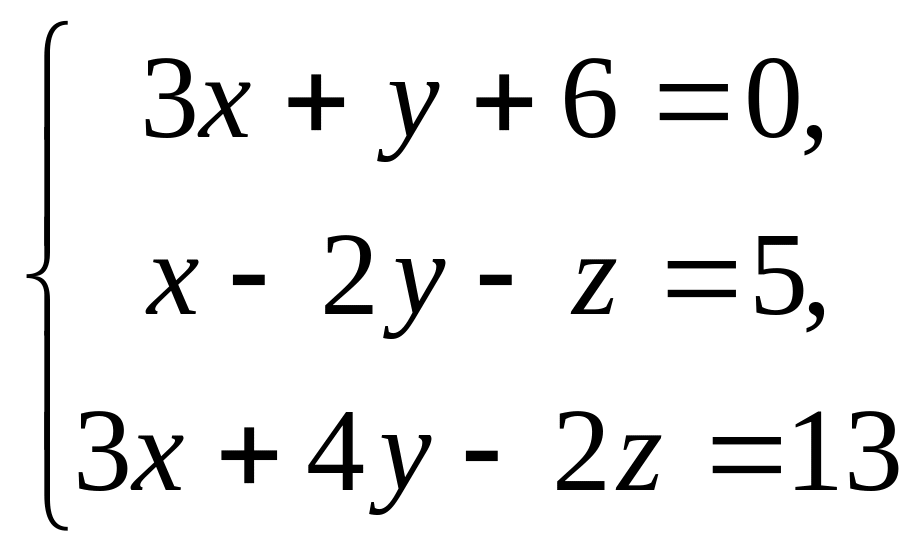
7.
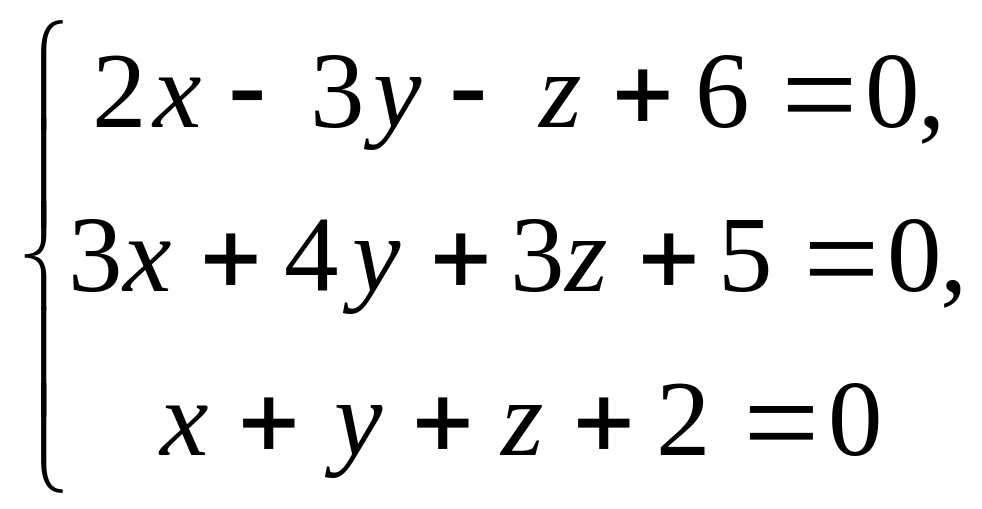 8.
8.
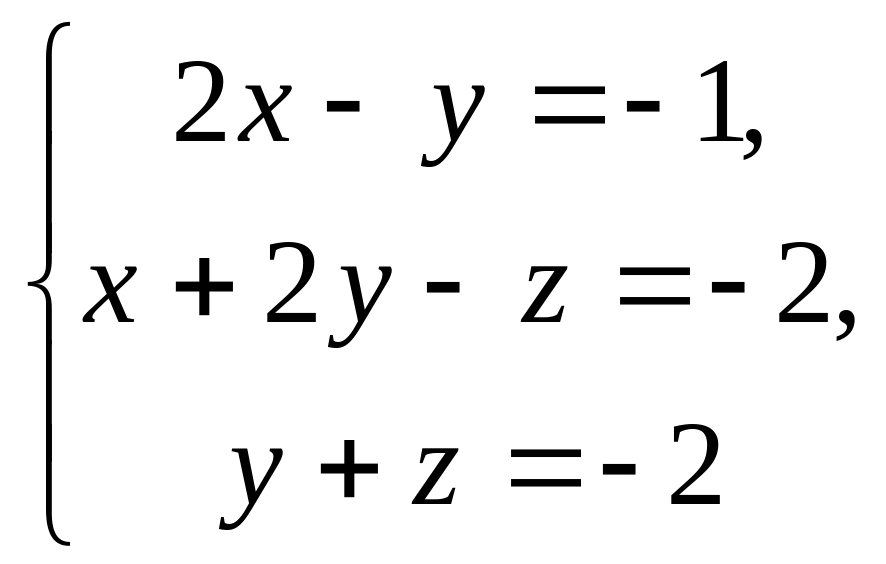 9.
9.

10.
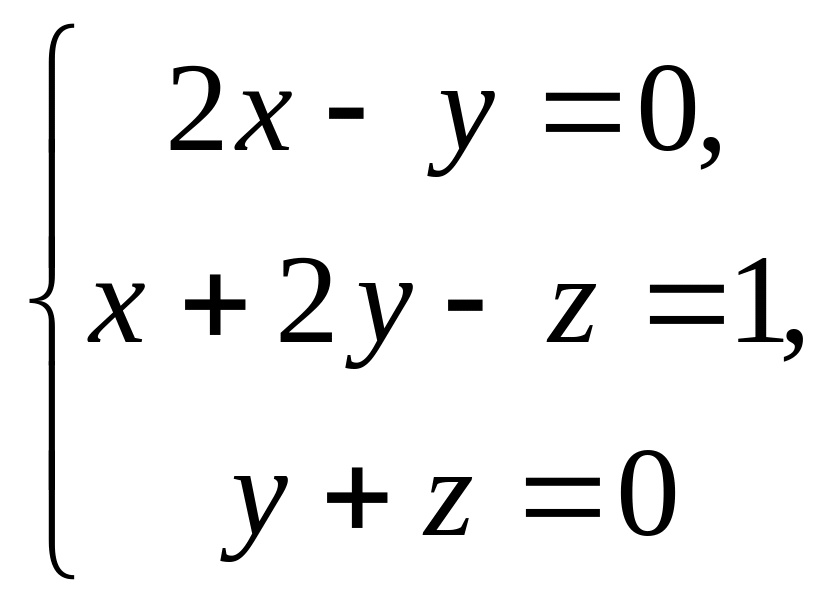 11.
11.
 12.
12.
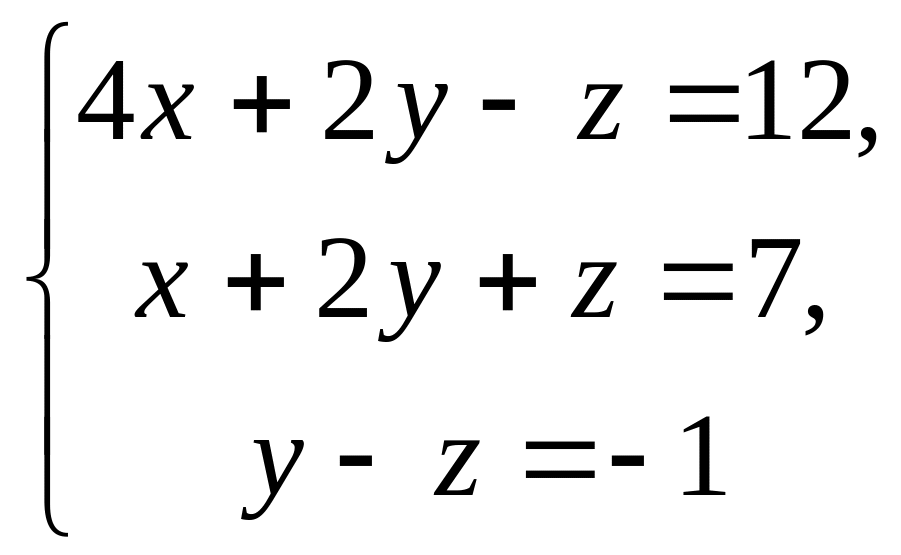
13.
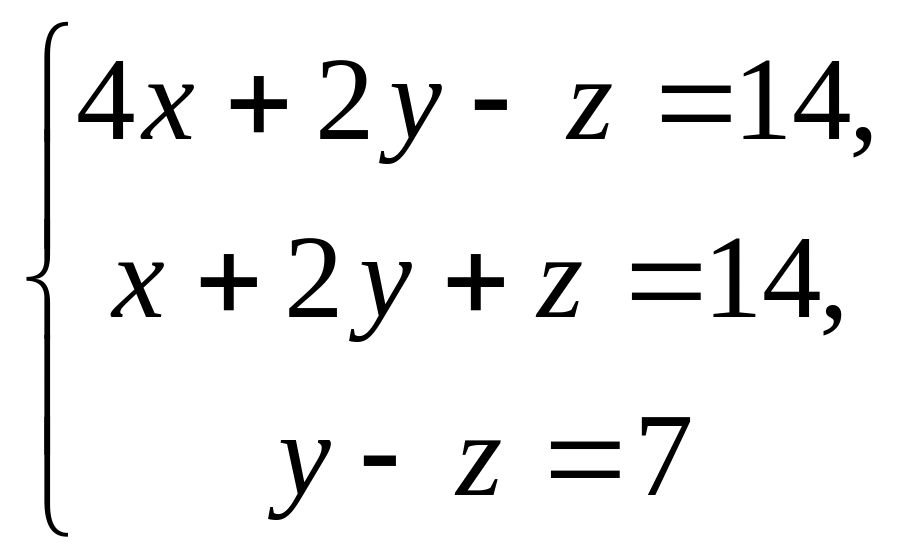 14.
14.
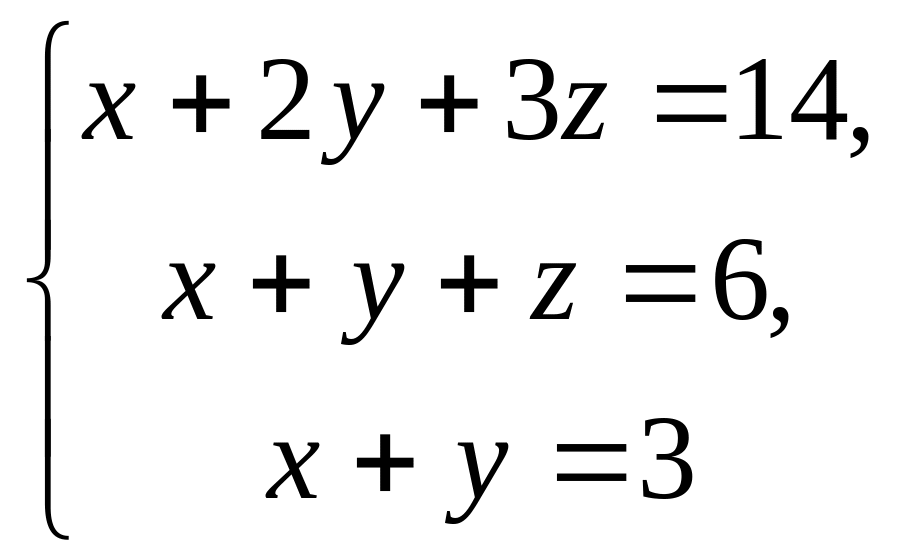 15.
15.
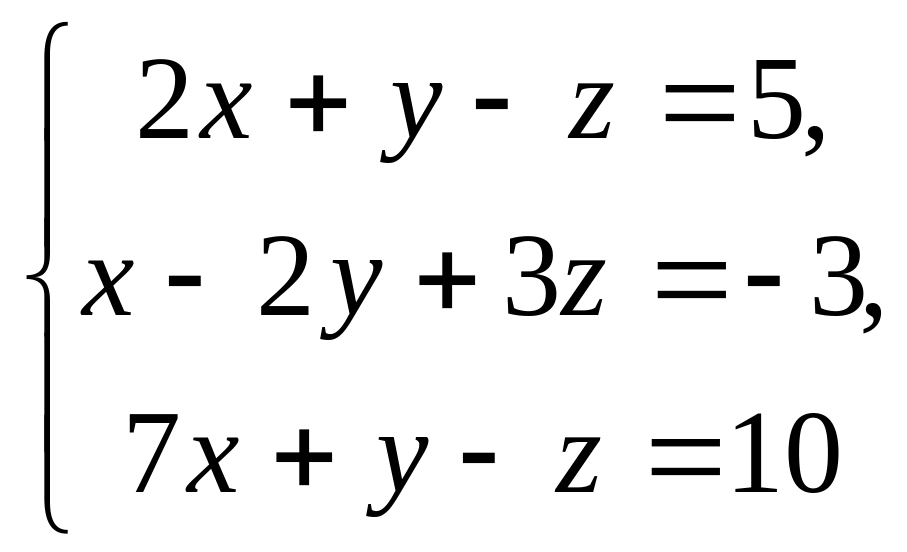
16.
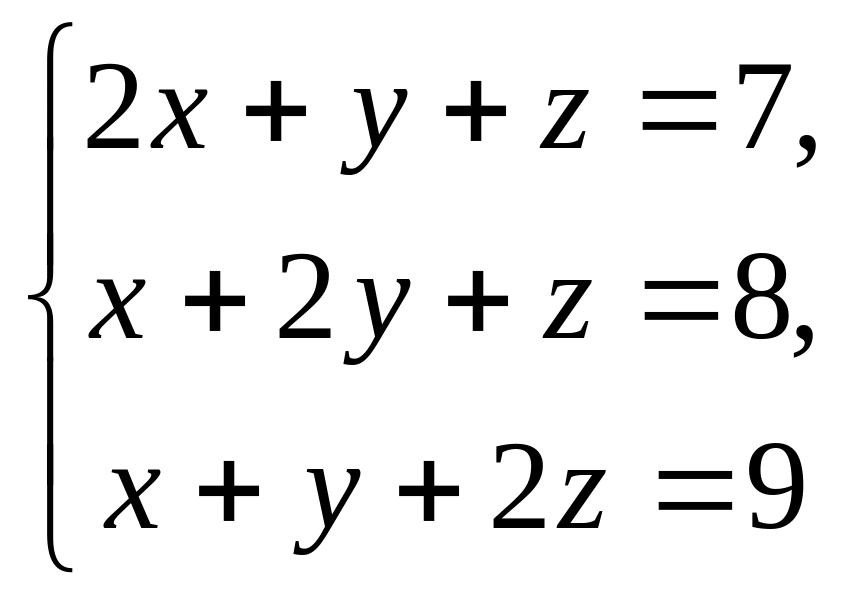 17.
17.
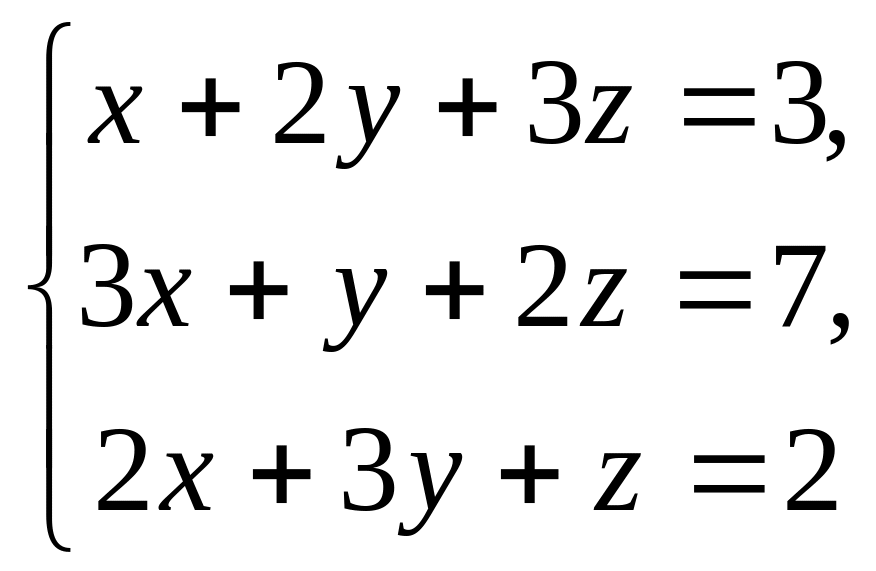 18.
18.
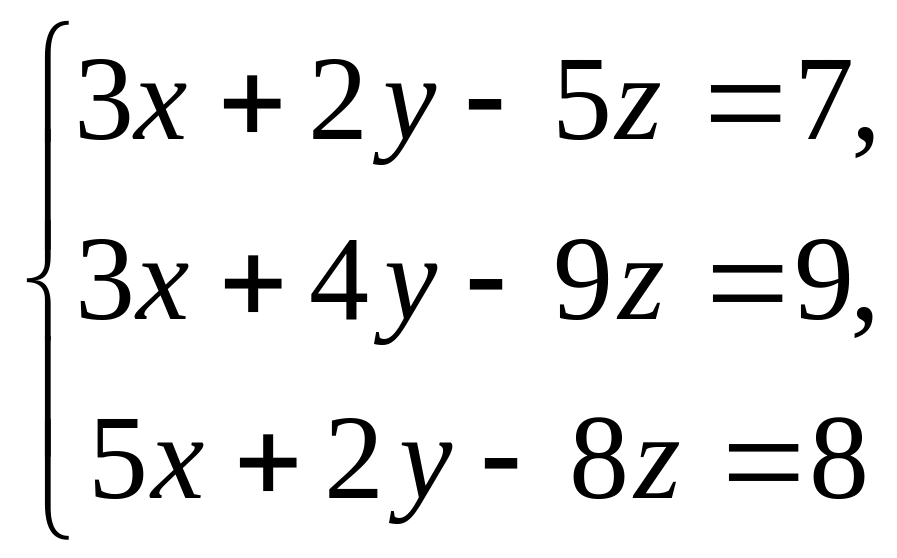
19.
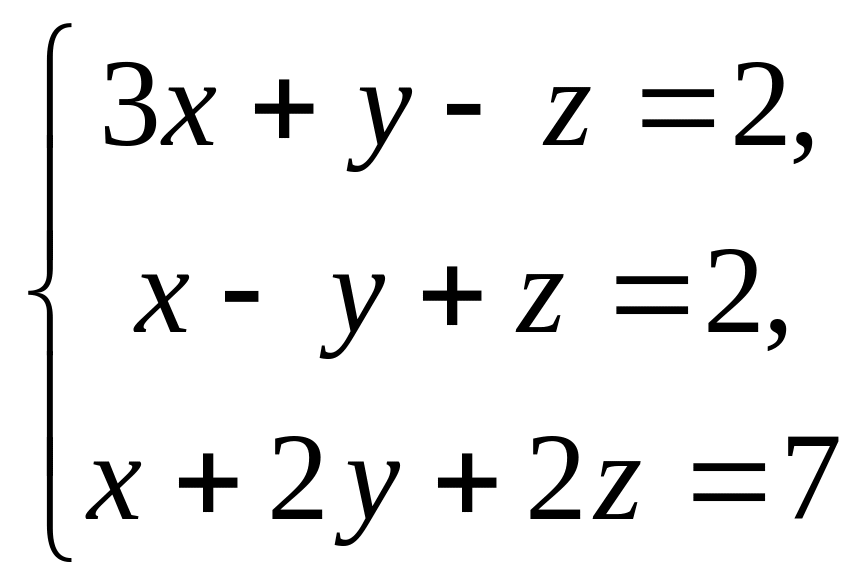 20.
20.
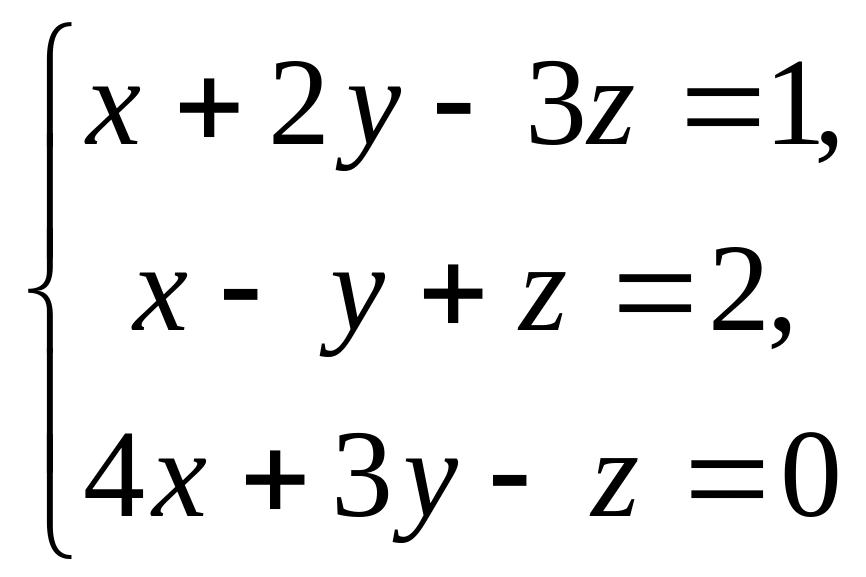 21.
21.
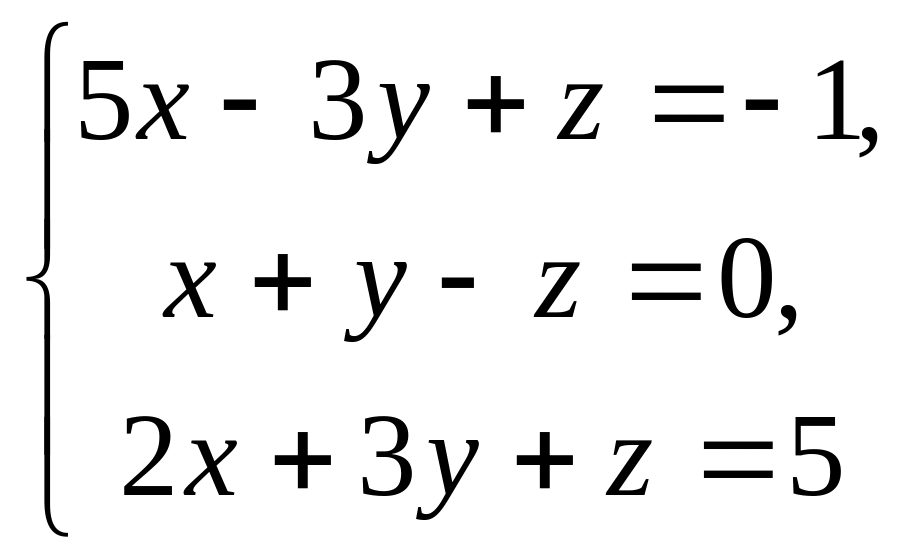
22.
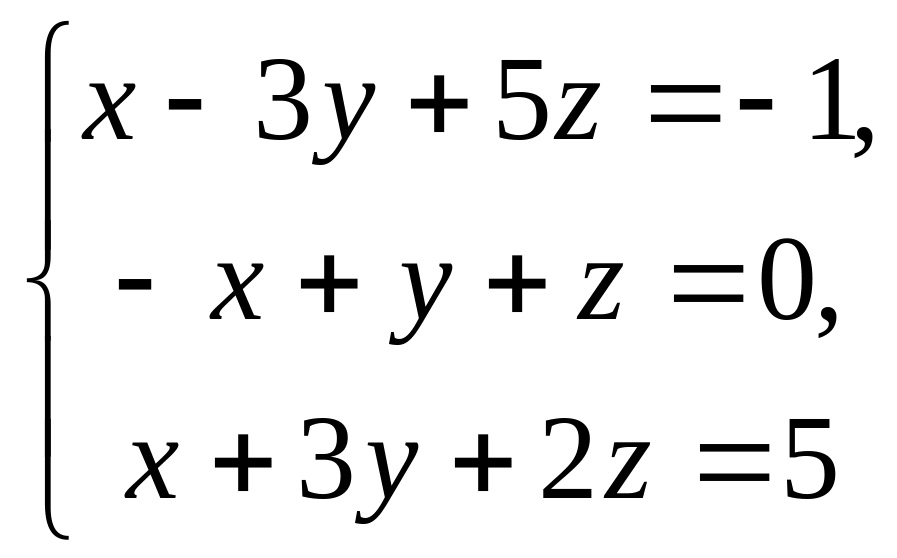 23.
23.
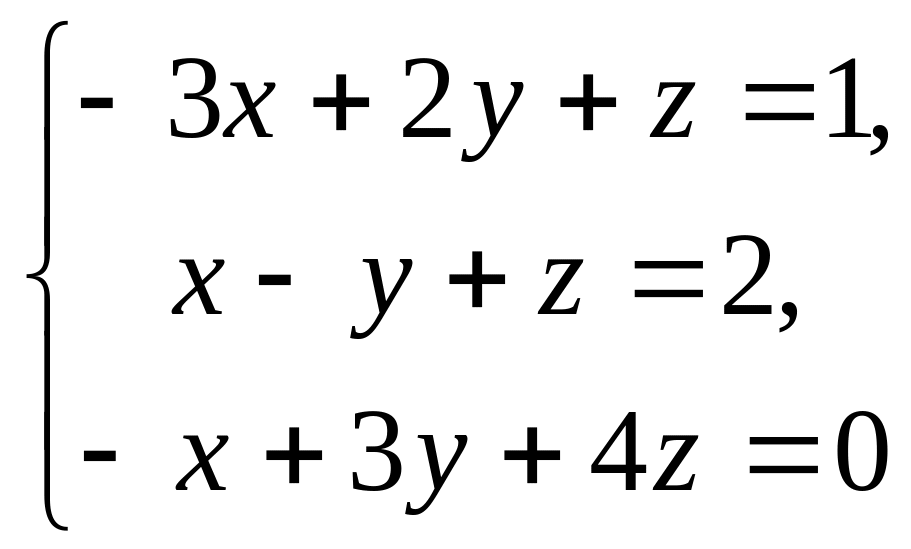 24.
24.
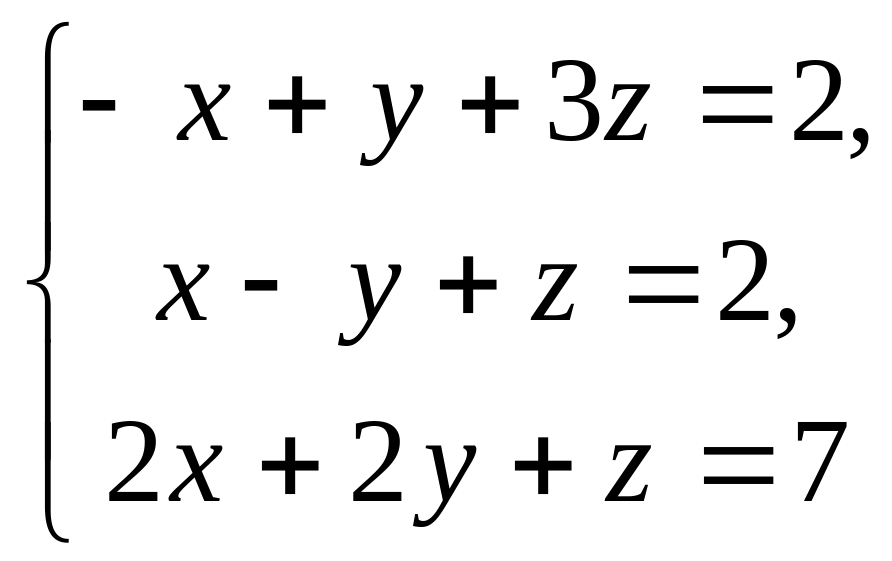
25.
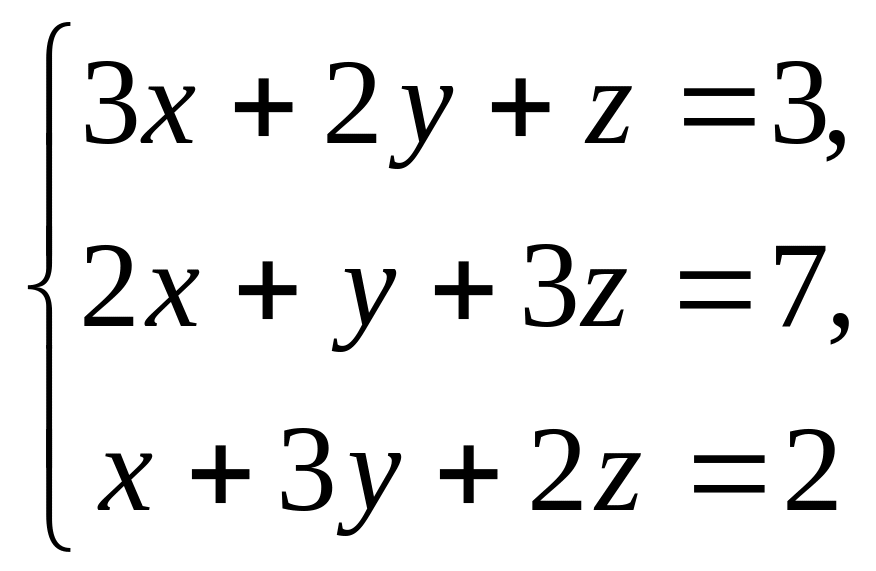 26.
26.
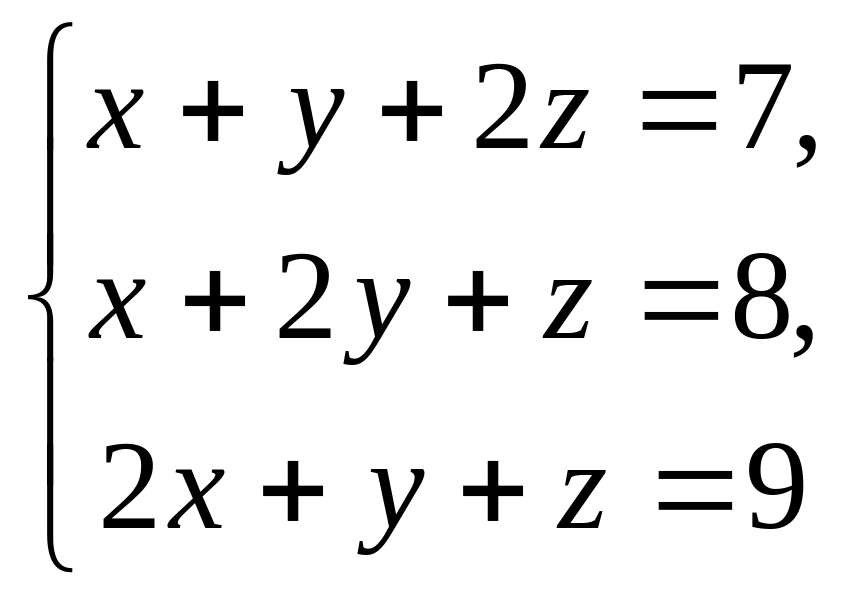 27.
27.
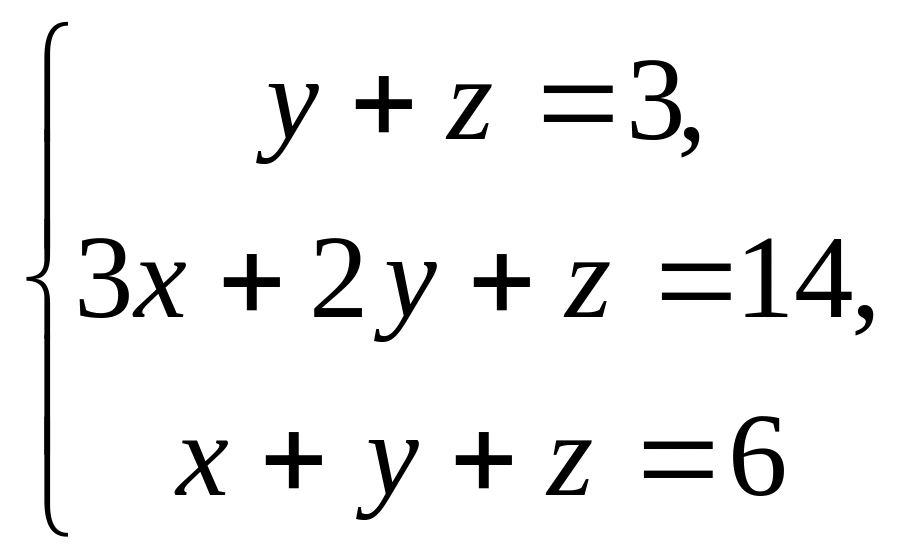
28.
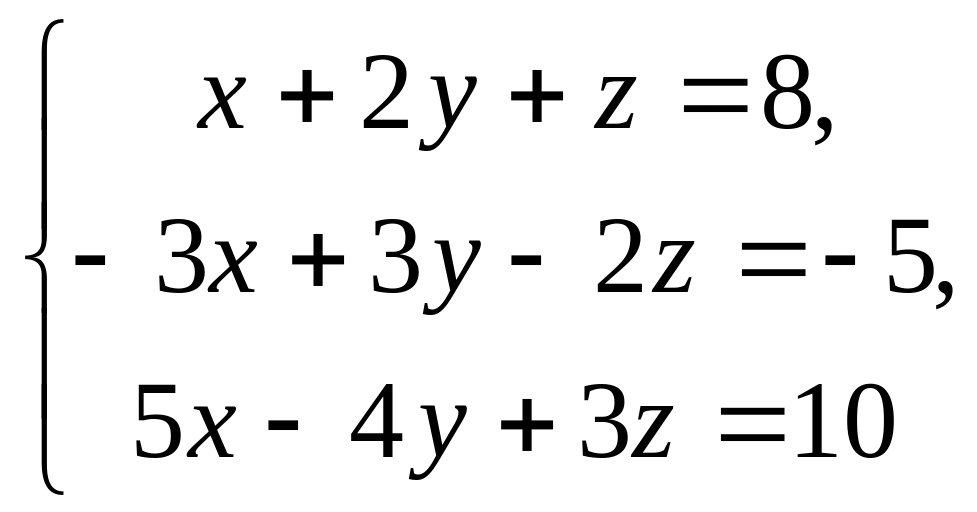 29.
29.
 30.
30.
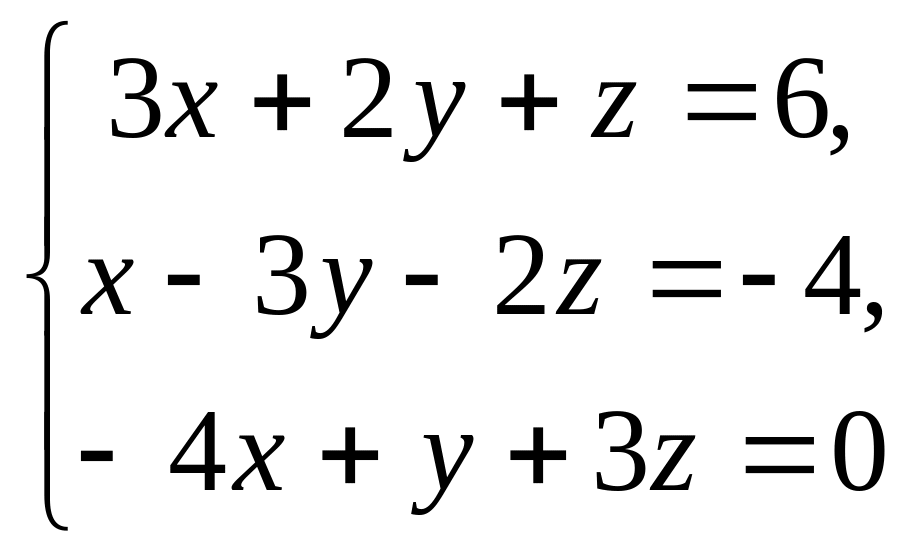
Задание 3. Вычислите определитель четвертого порядка.
1.
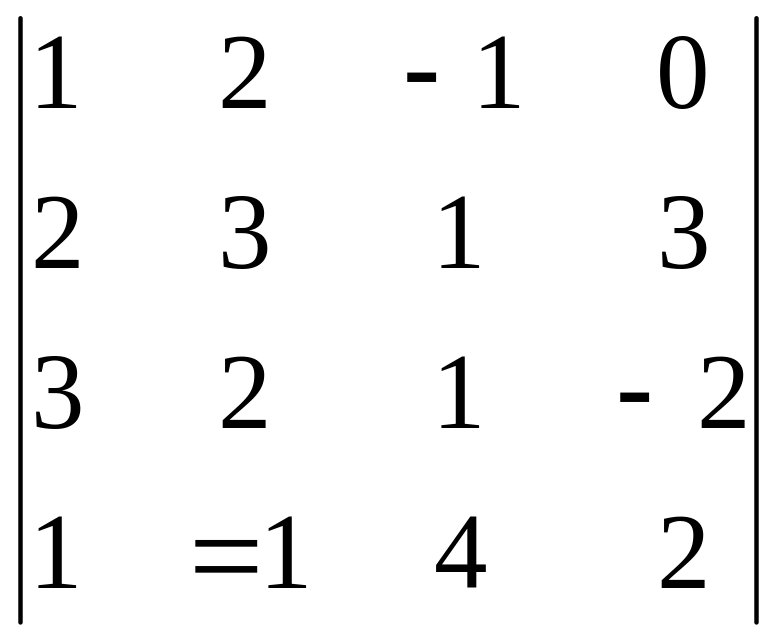 2.
2.
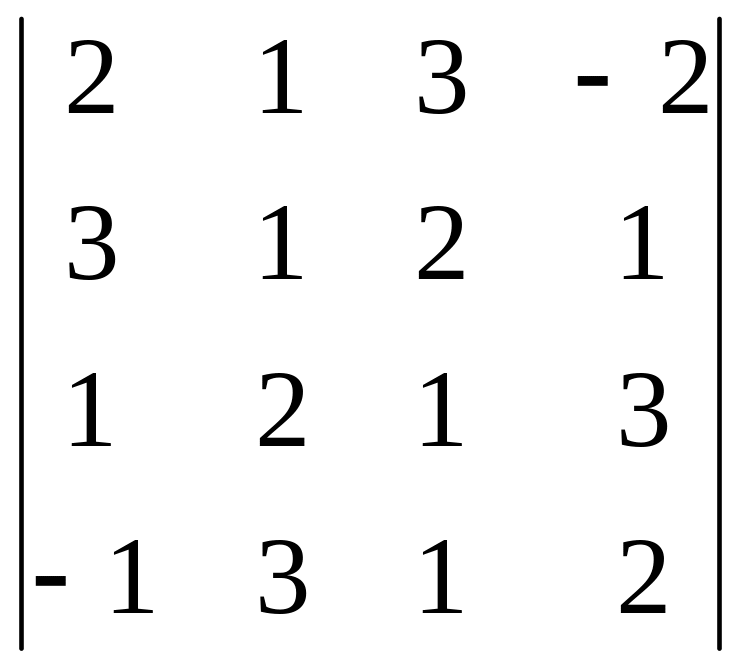 3.
3.
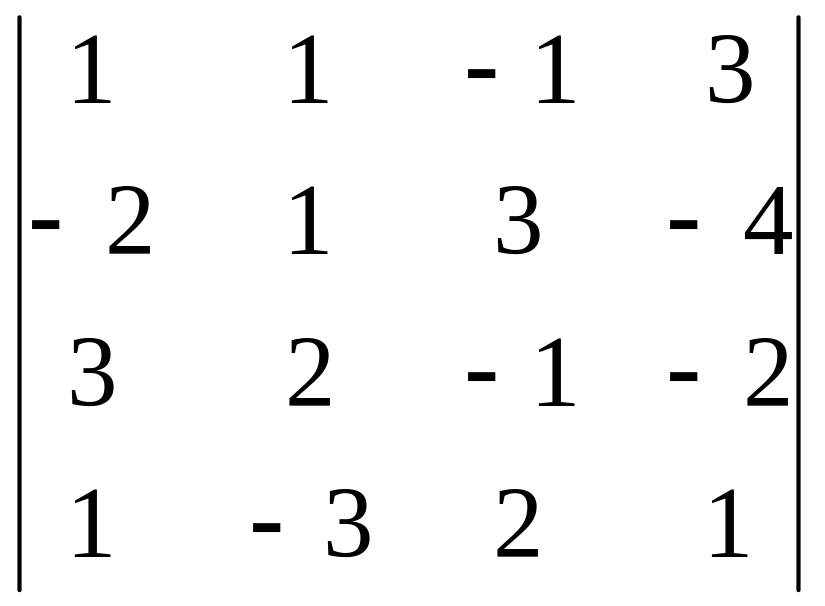
4.
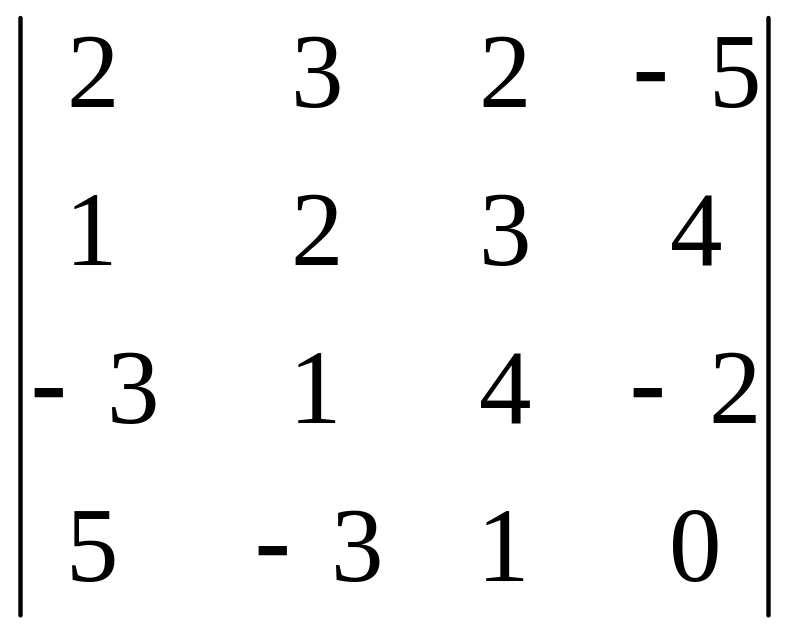 5.
5.
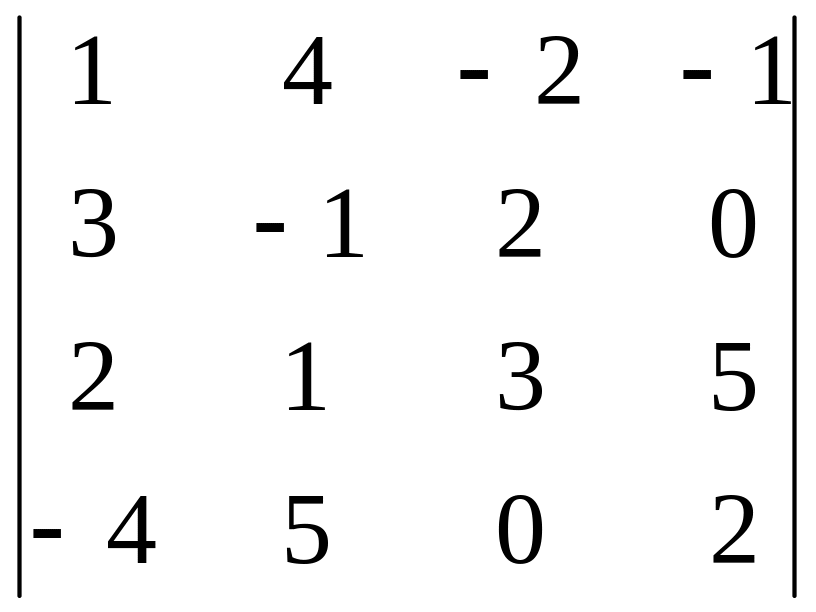 6.
6.
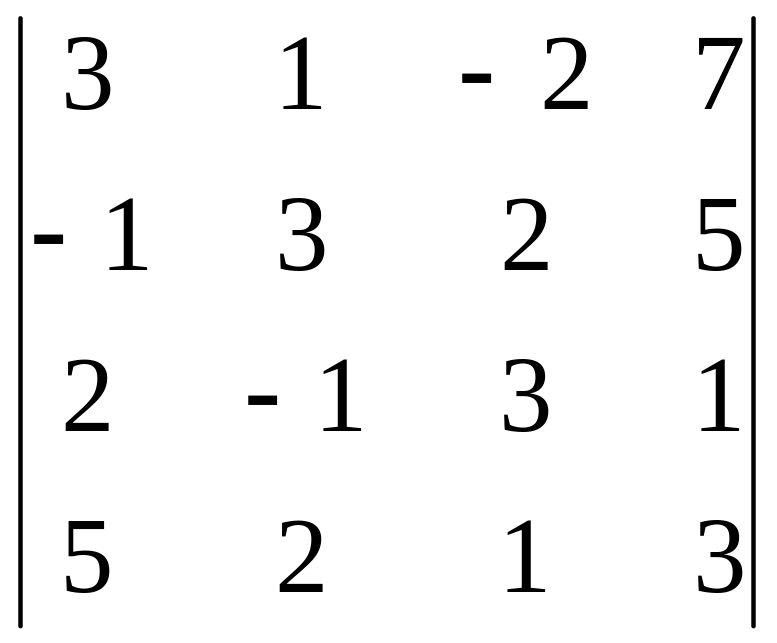
7.
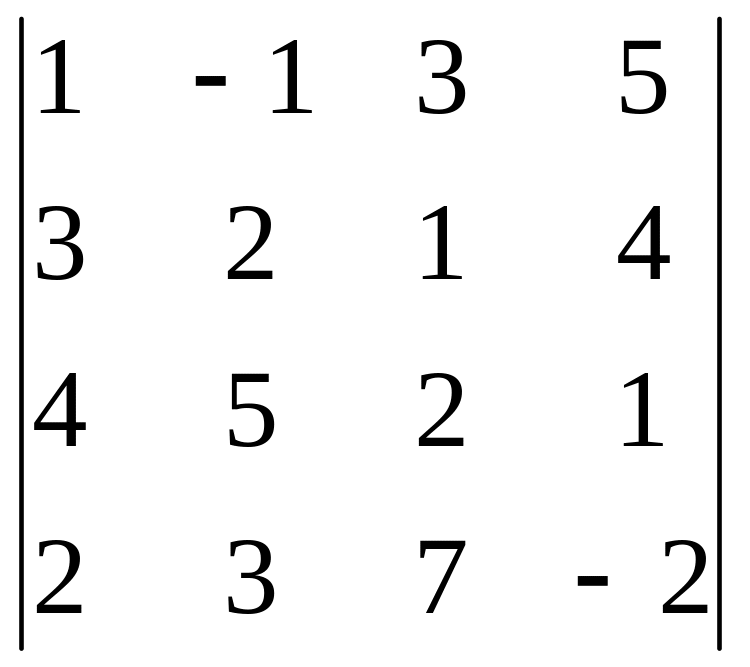 8.
8.
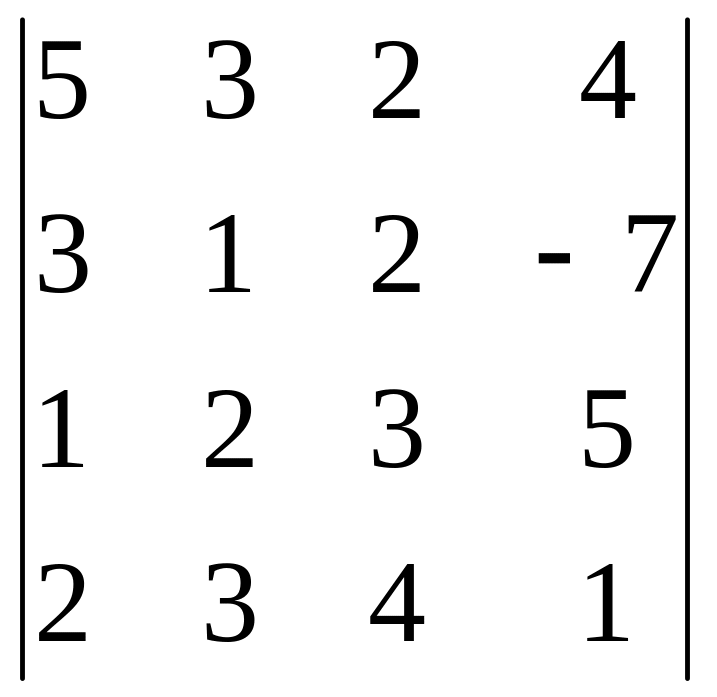 9.
9.
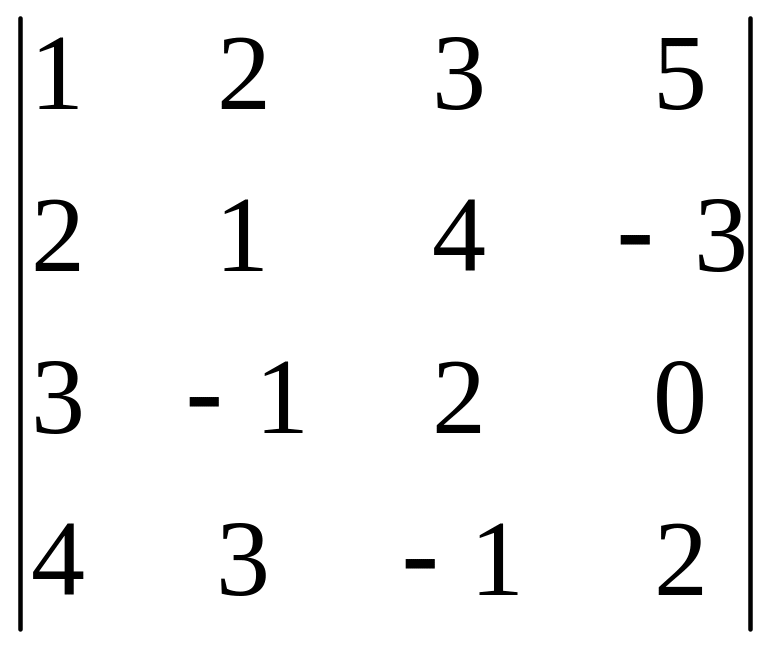
10.
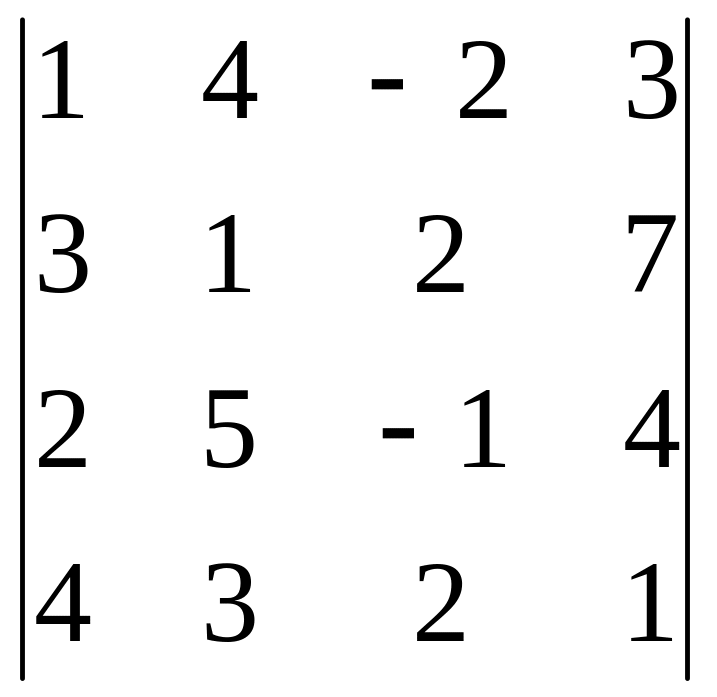 11.
11.
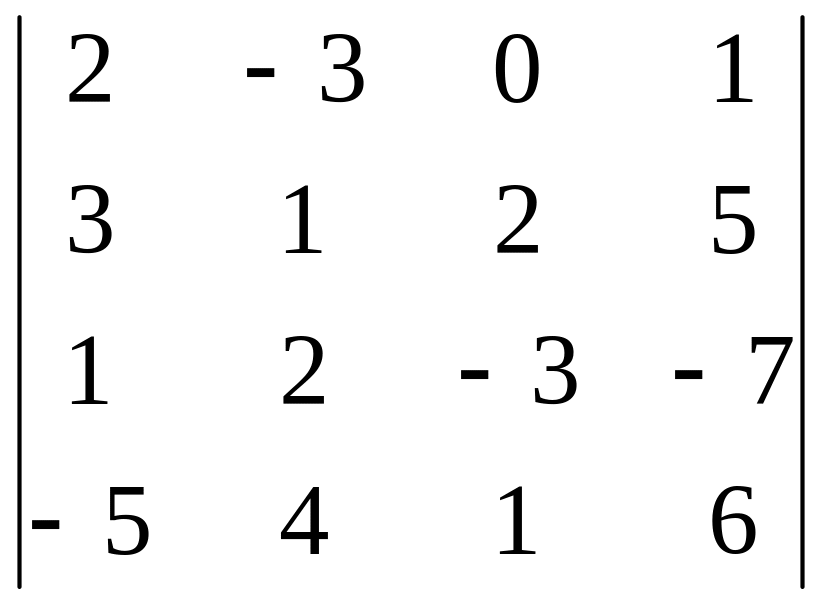 12.
12.
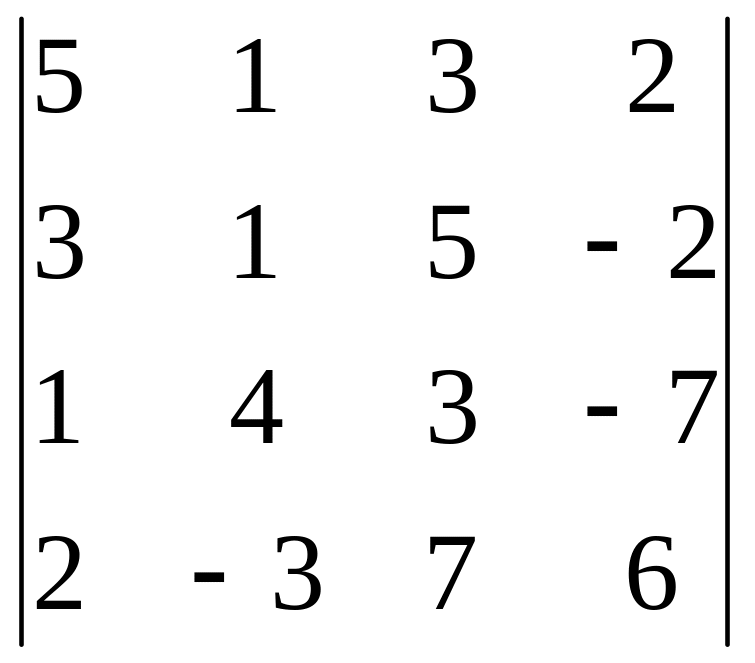
13.
 14.
14.
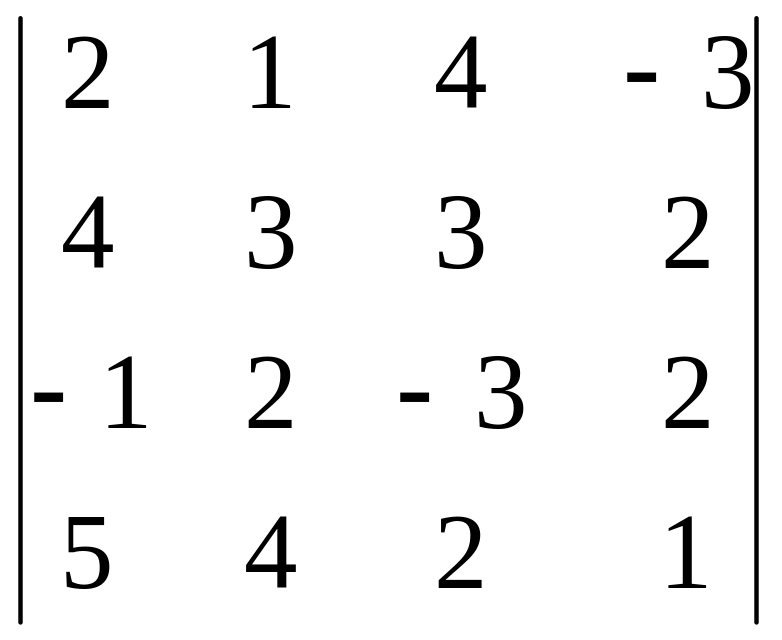 15.
15.
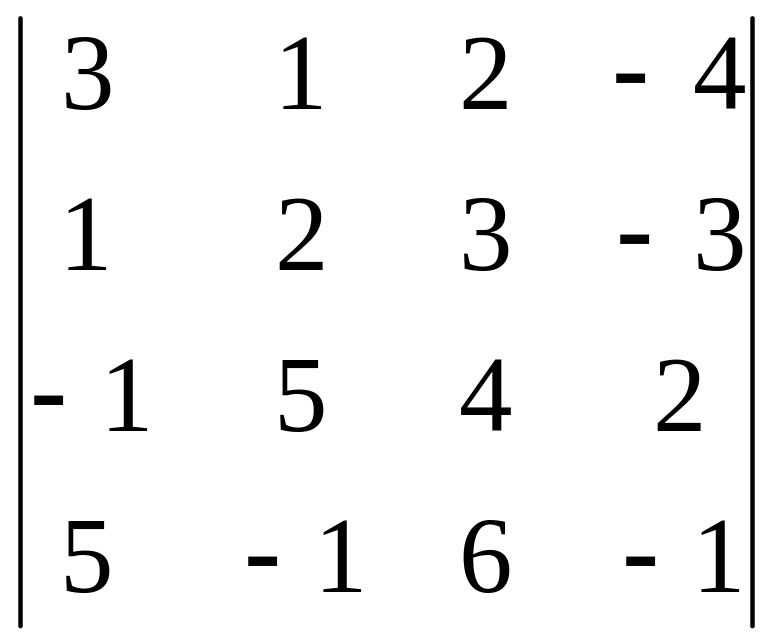
16.
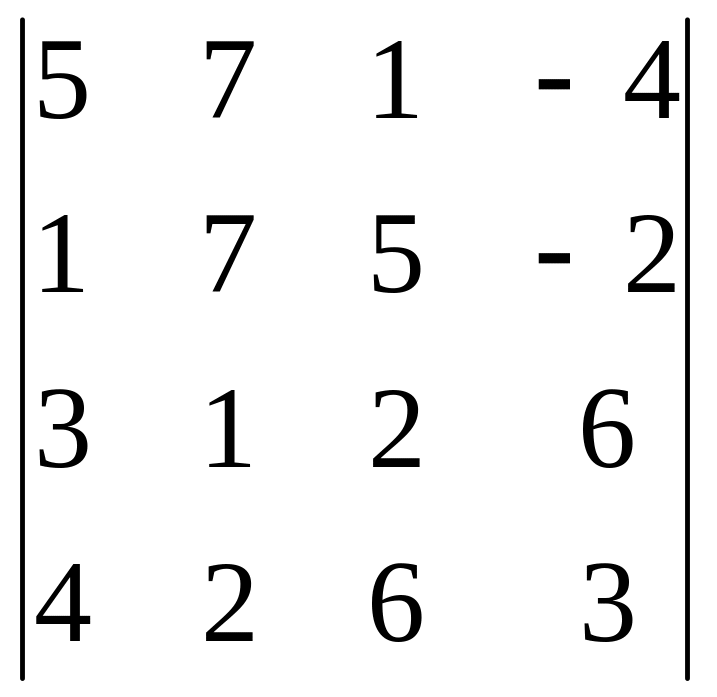 17.
17.
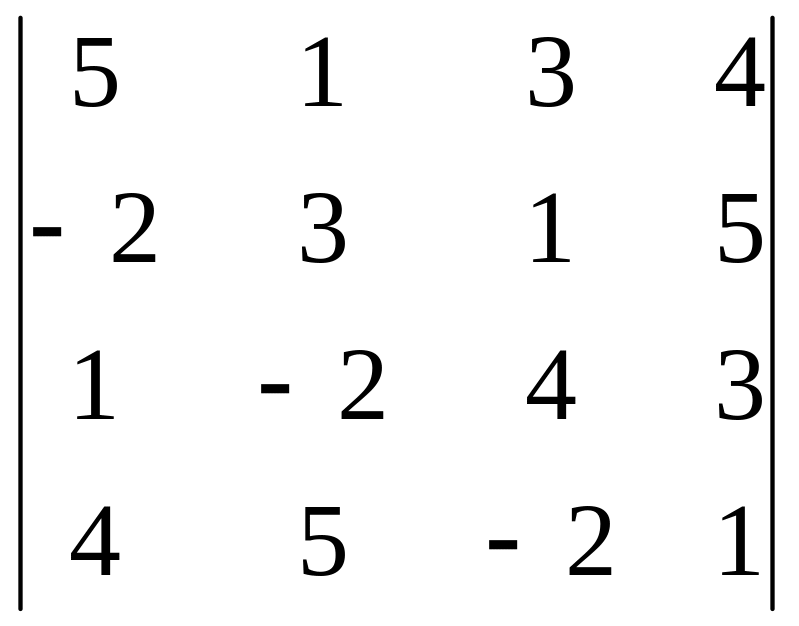 18.
18.
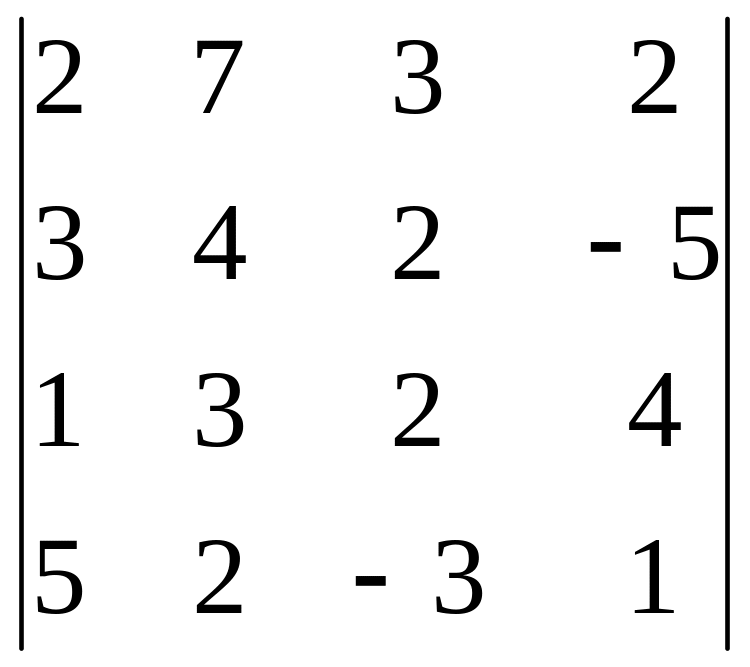
19.
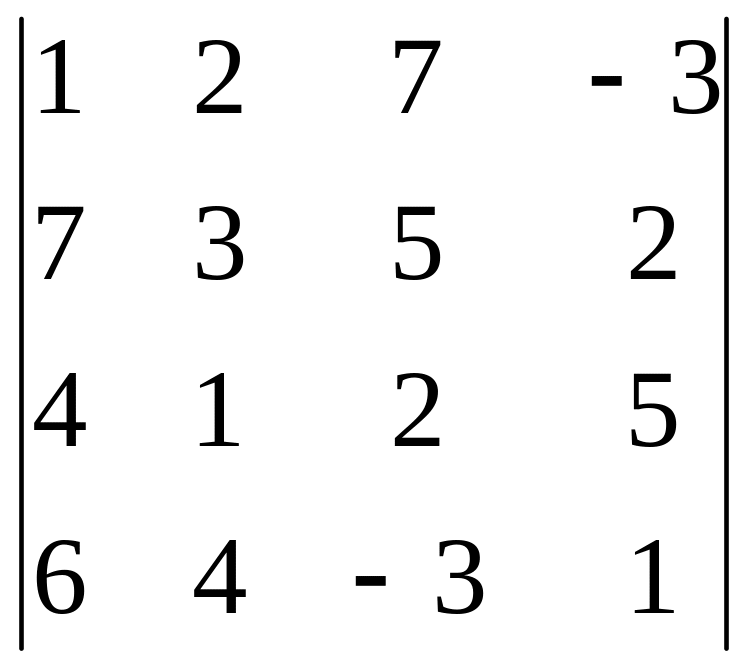 20.
20.
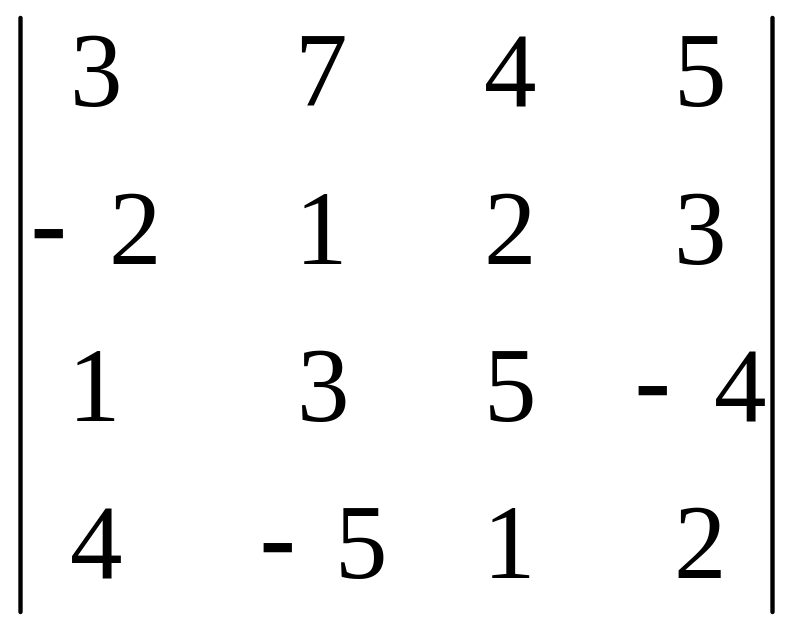 21.
21.
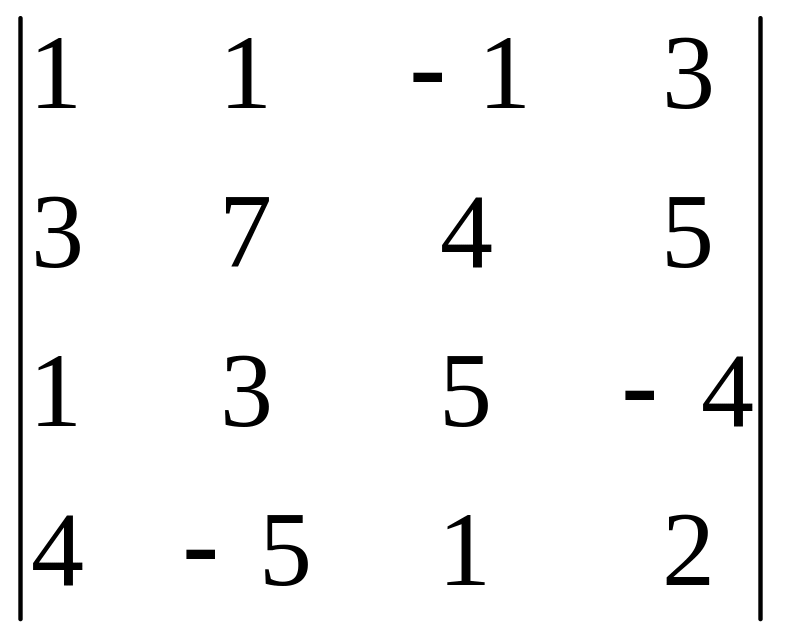
22.
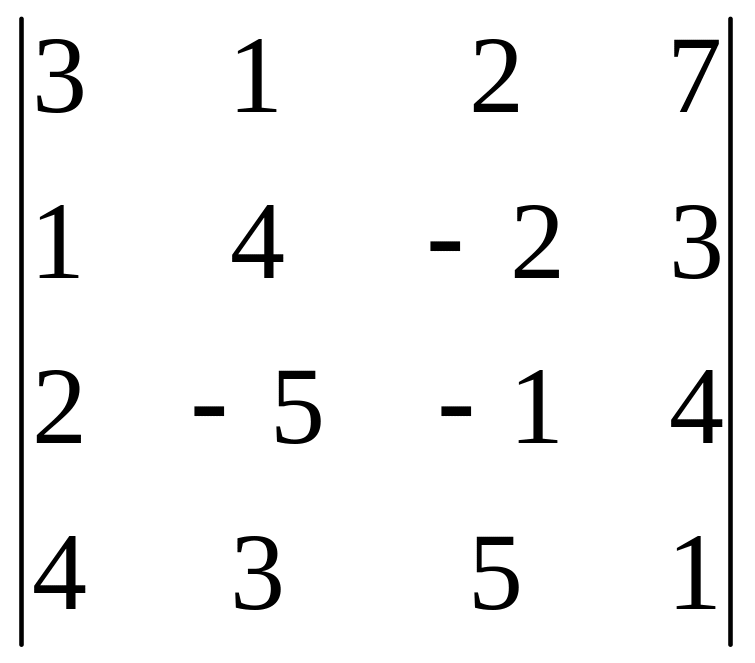 23.
23.
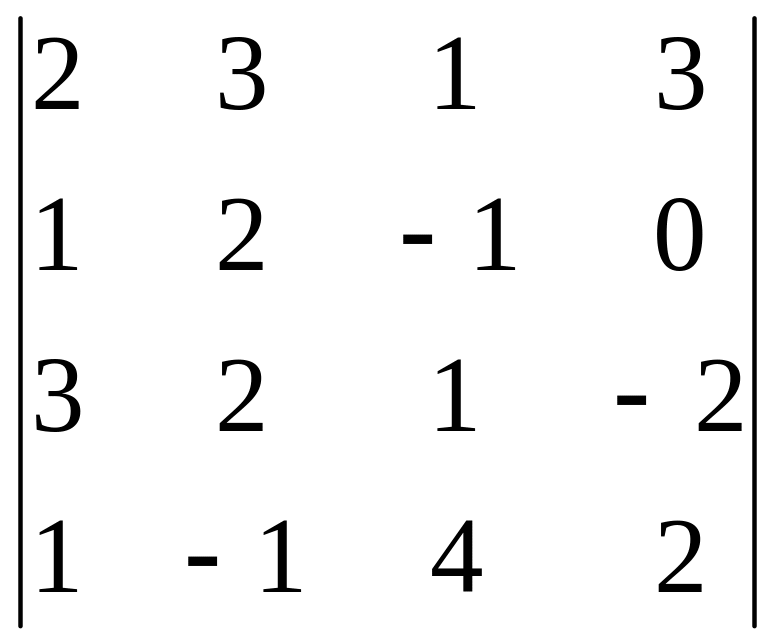 24.
24.

25.
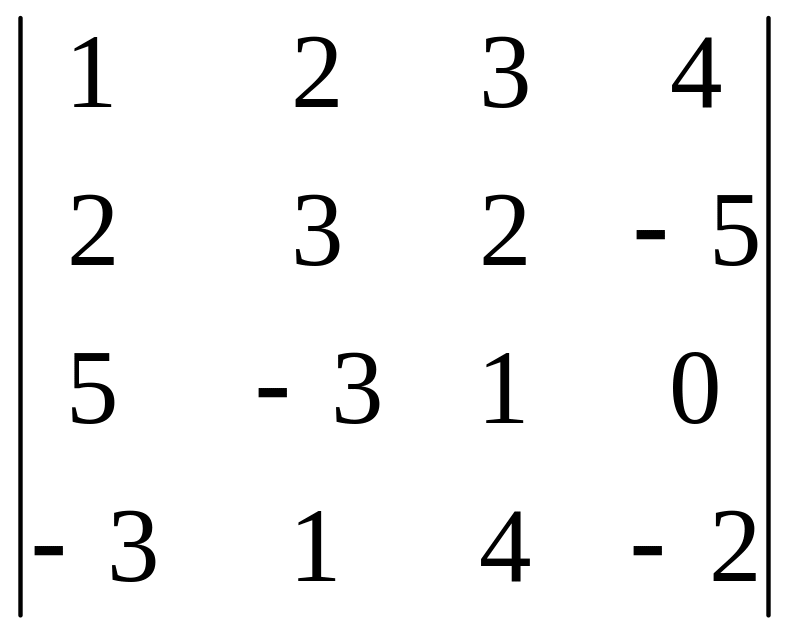 26.
26.
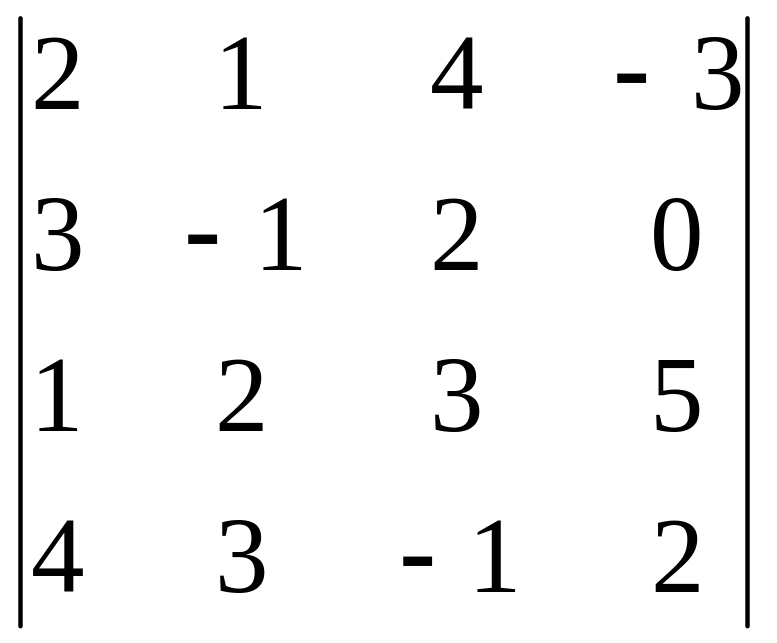 27.
27.
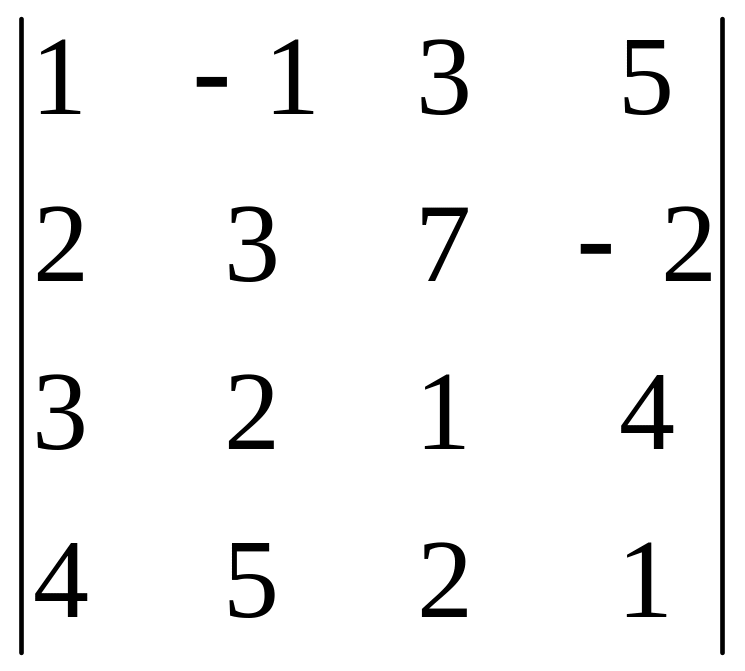
28.
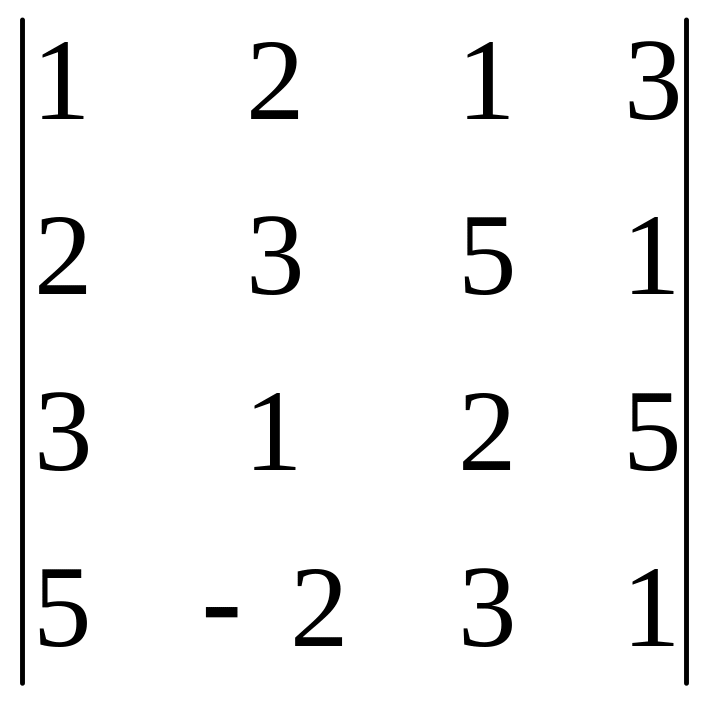 29.
29.
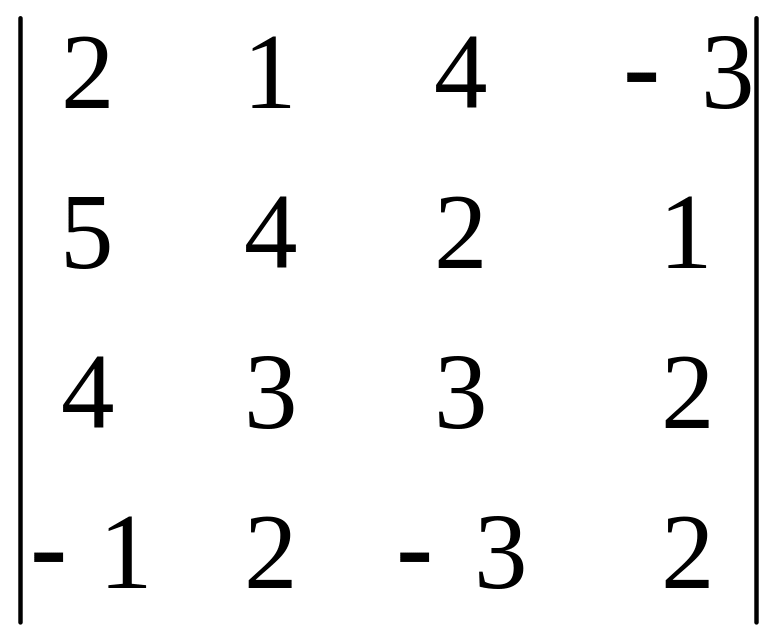 30.
30.
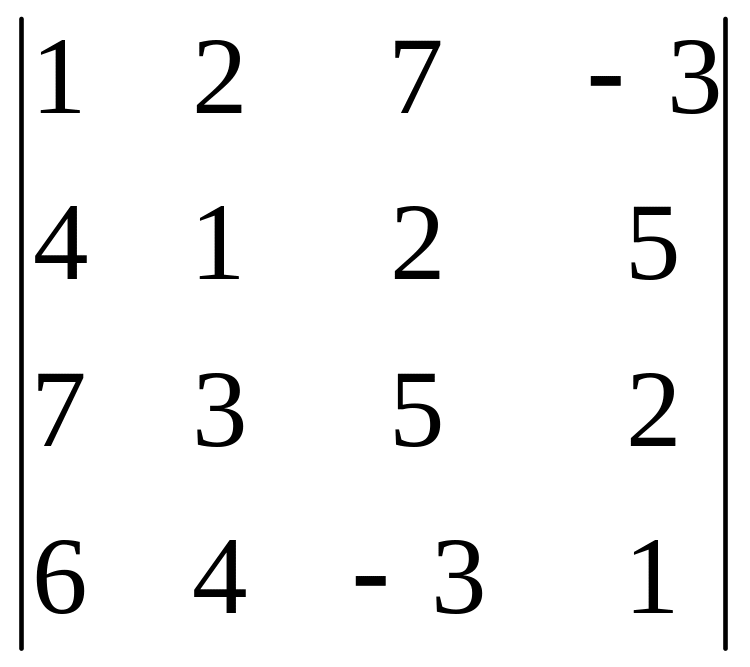
Задание
4. Найдите
матрицу
![]() ,
если:
,
если:
1.
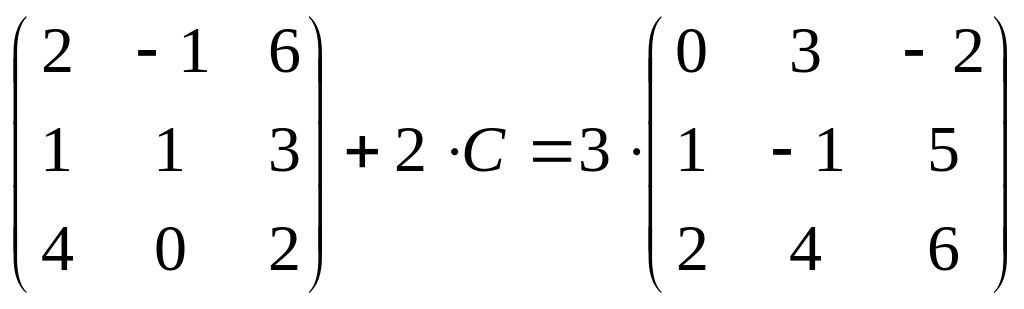 ;
;
2.
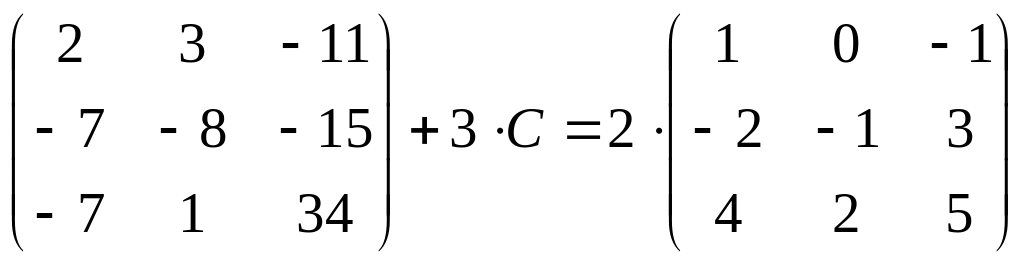 ;
;
3.
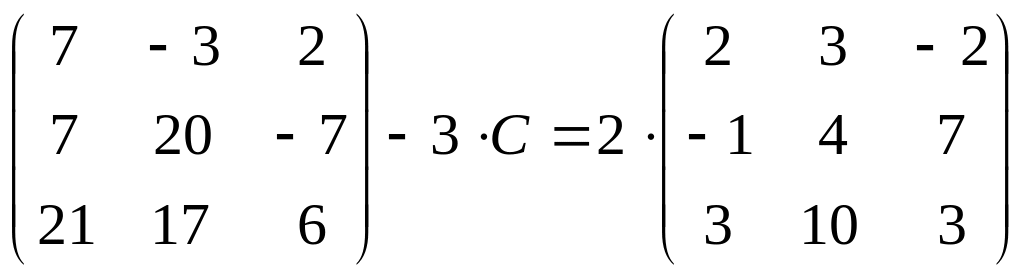 ;
;
4.
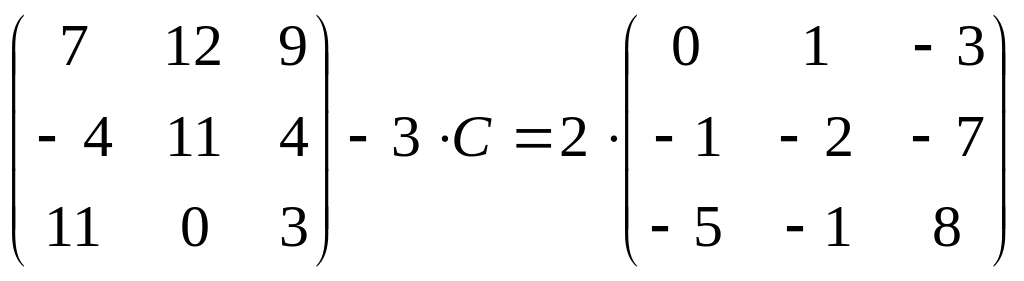 ;
;
5.
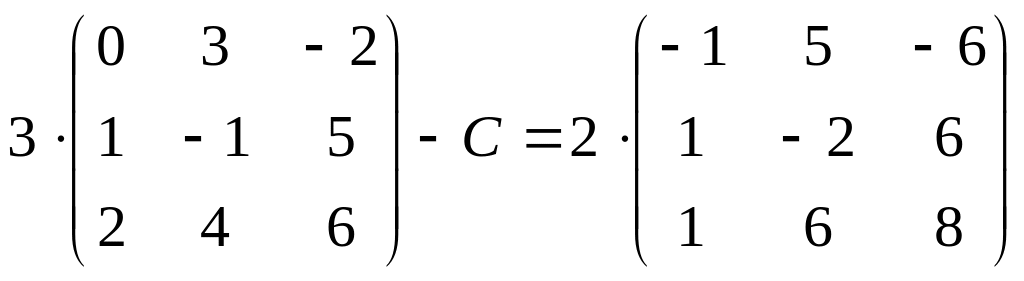 ;
;
6.
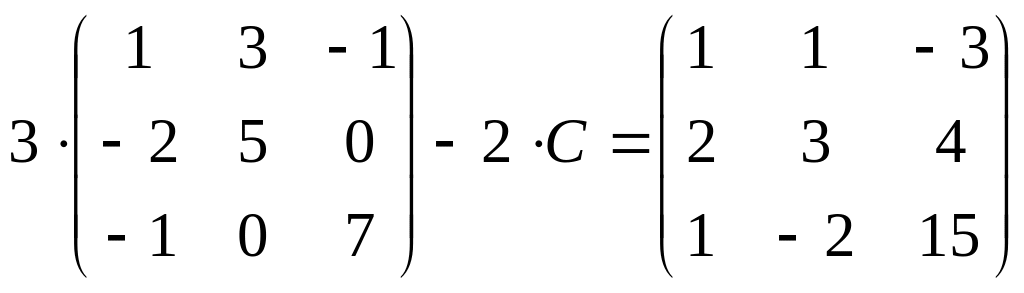 ;
;
7.
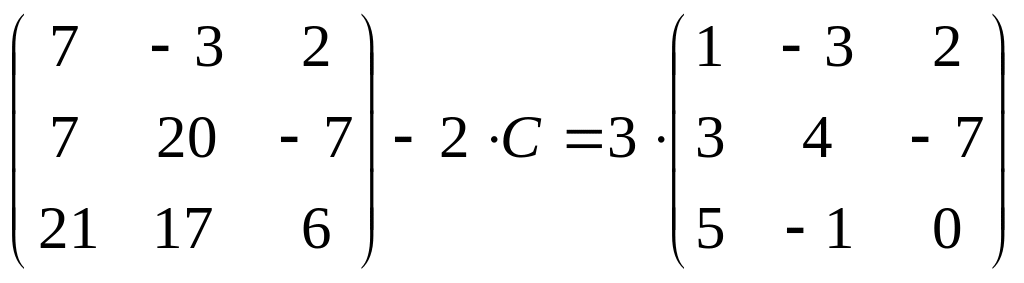 ;
;
8.
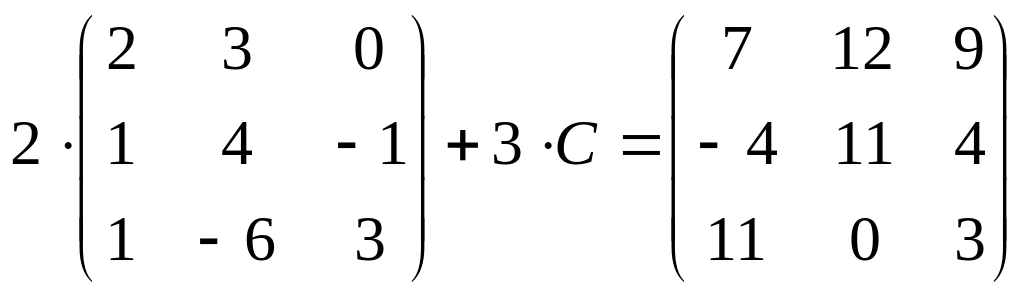 ;
;
9.
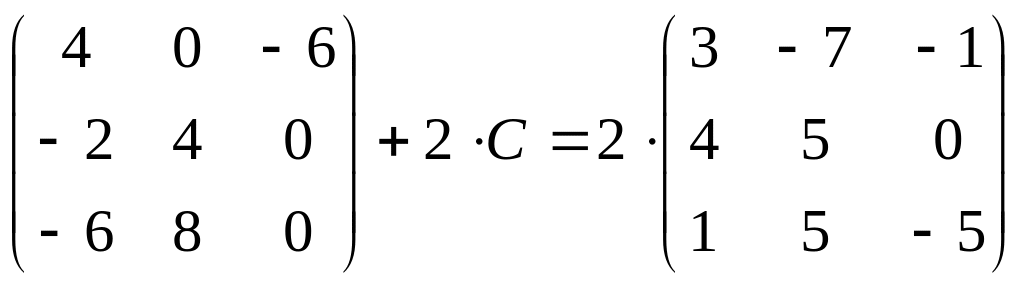 ;
;
10.
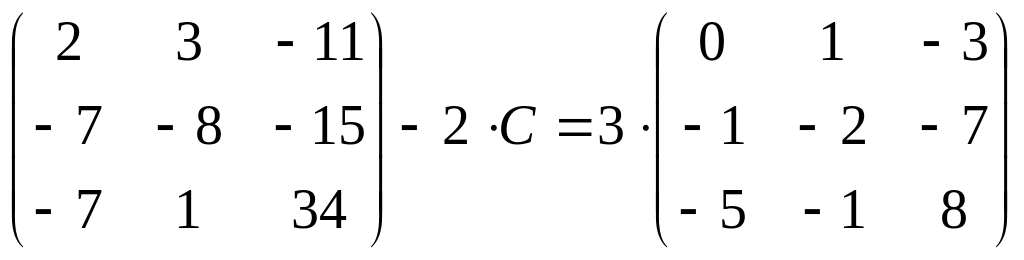 ;
;
11.
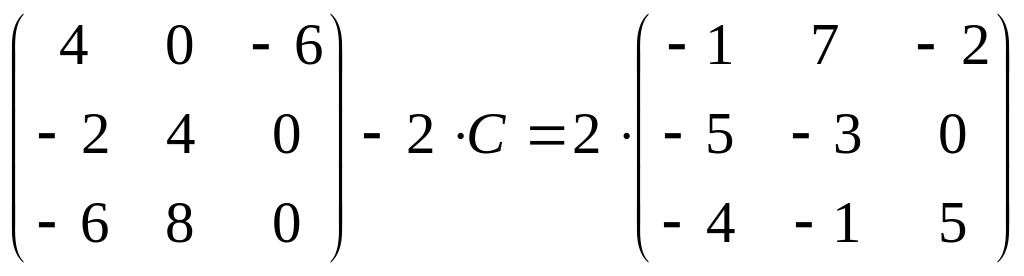 ;
;
12.
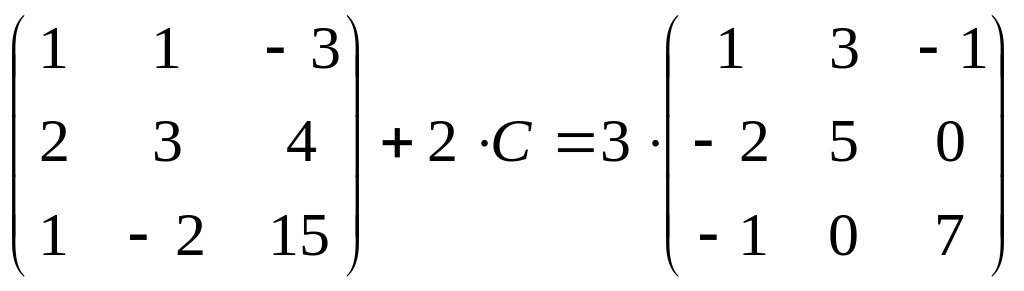 ;
;
13.
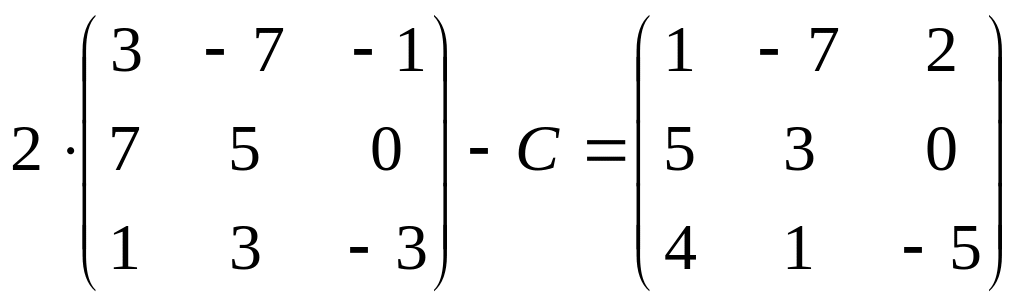 ;
;
14.
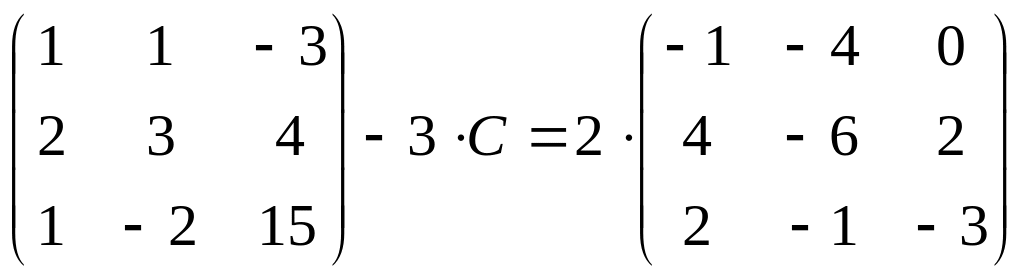 ;
;
15.
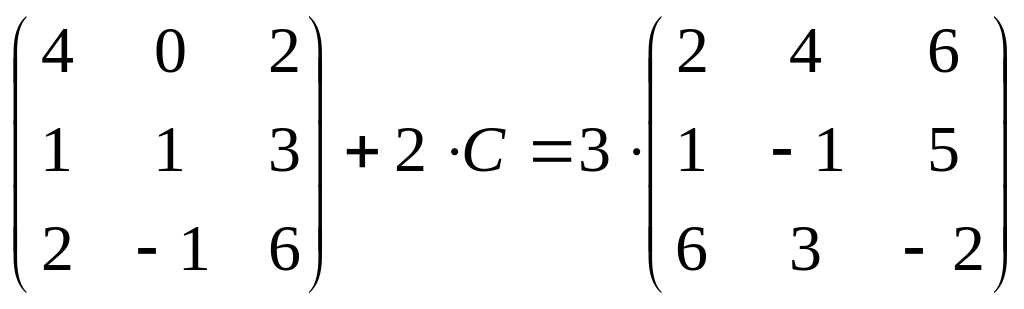 ;
;
16.
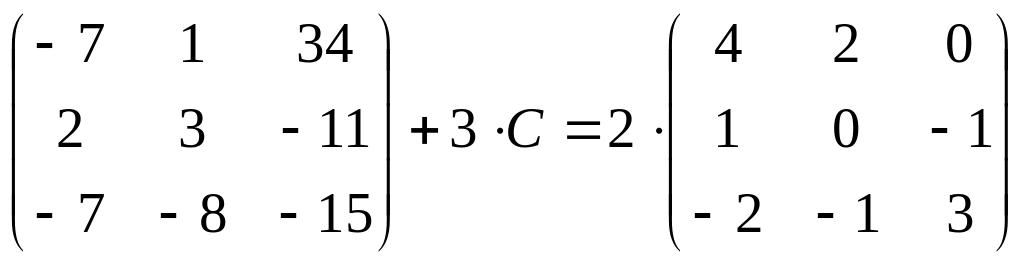 ;
;
17.
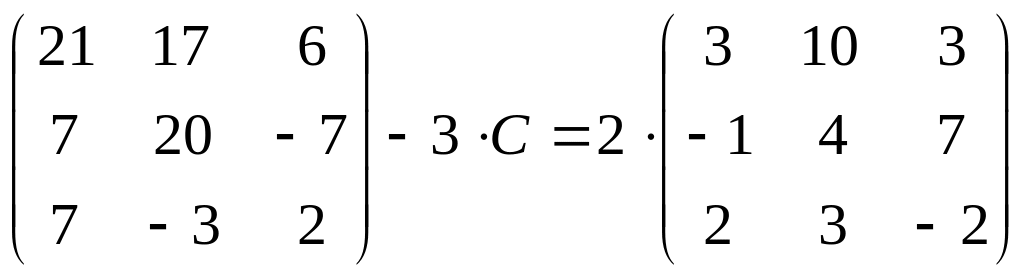 ;
;
18.
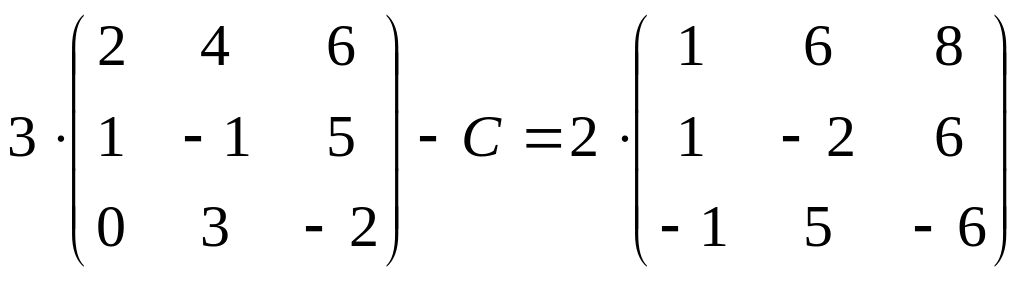 ;
;
19.
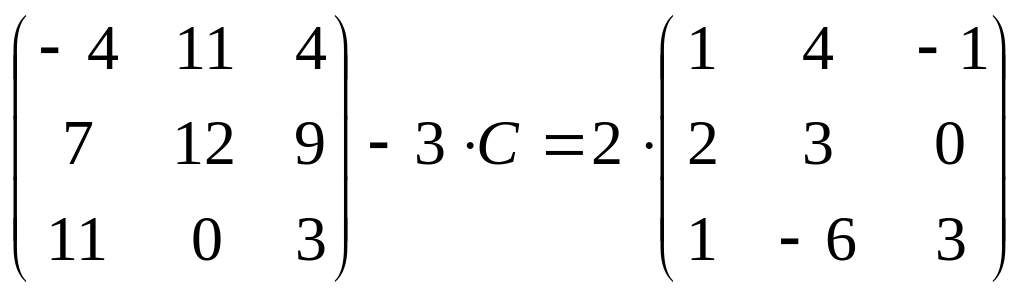 ;
;
20.
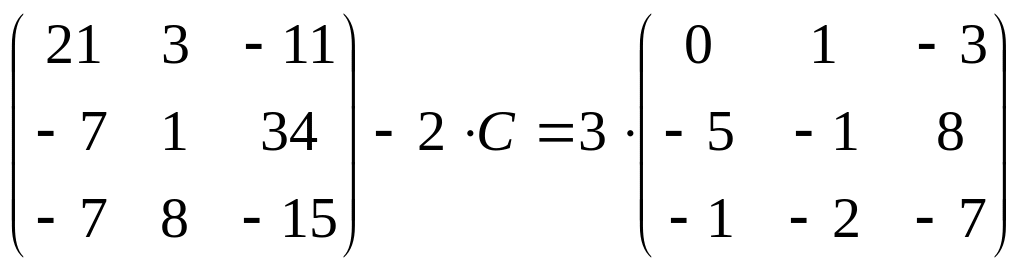 ;
;
21.
 ;
;
22.
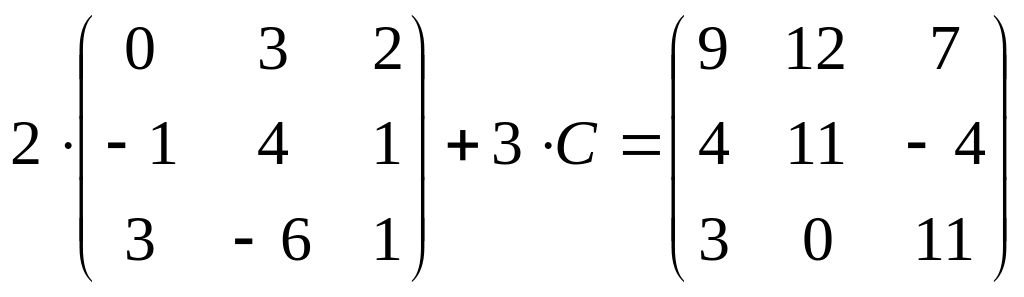 ;
;
23.
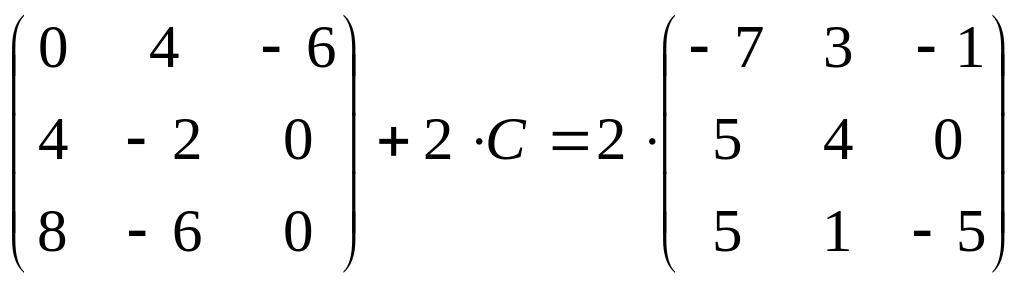 ;
;
24.
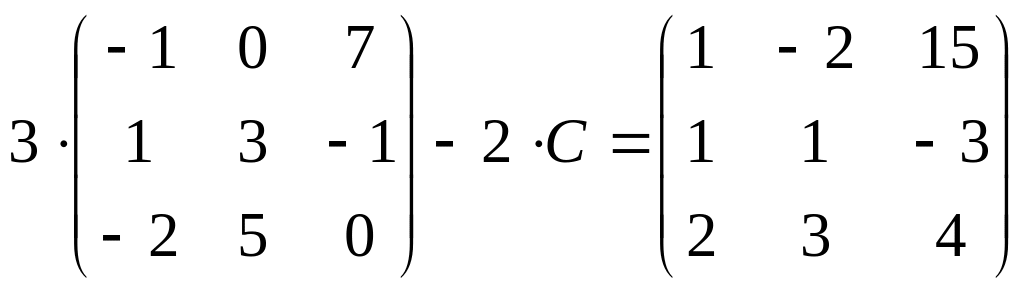 ;
;
25.
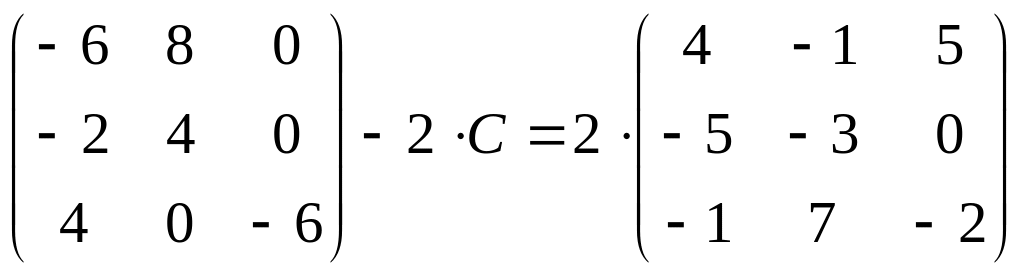 ;
;
26.
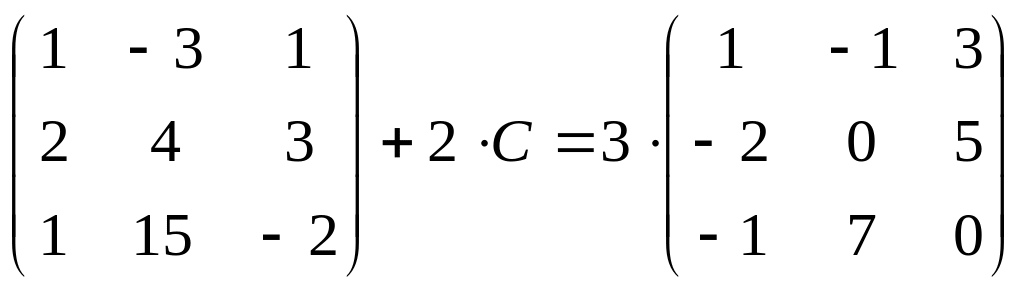 ;
;
27. ;
28.
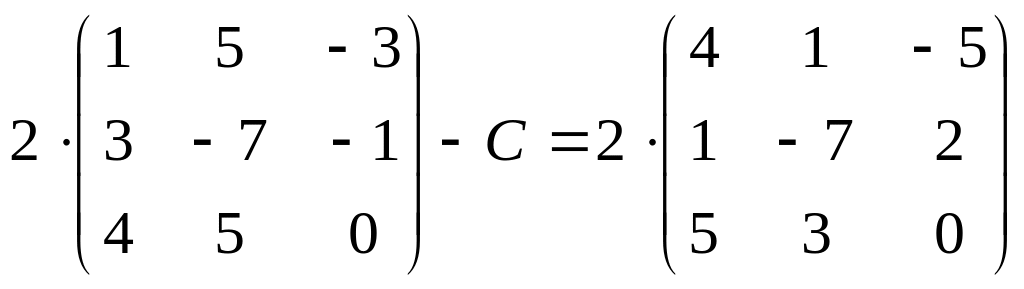 ;
;
29.
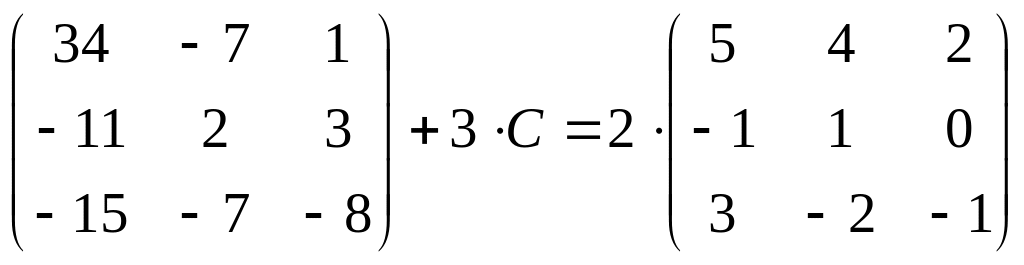 ;
;
30.
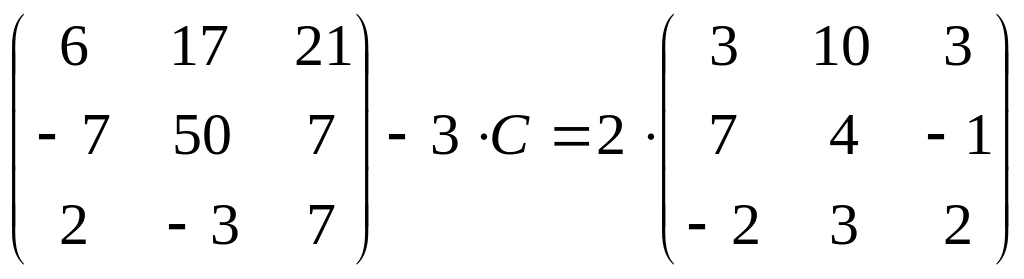 .
.
Задание 5. Решите матричные уравнения и проверьте подстановкой:
1.
a)![]() ;
б)
;
б)
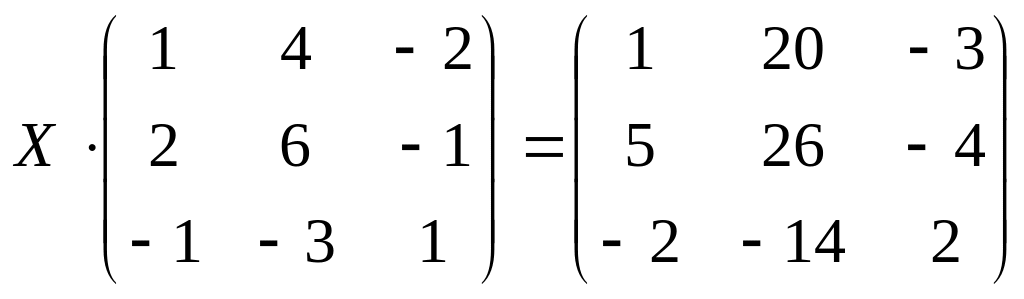 ;
;
2.
а)
![]() ;
б)
;
б)
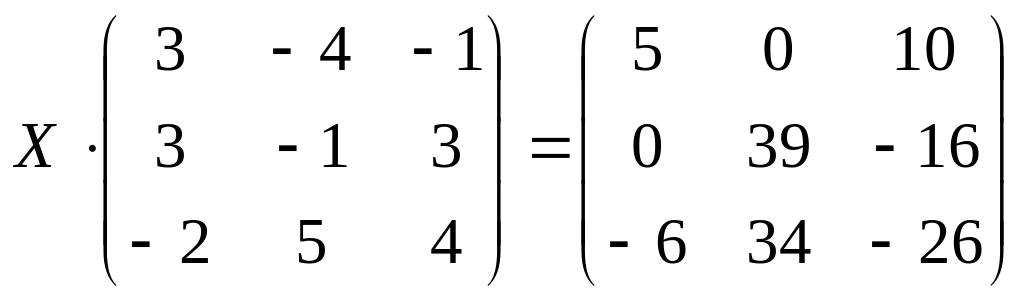 ;
;
3.
а)
![]() ;
б)
;
б)
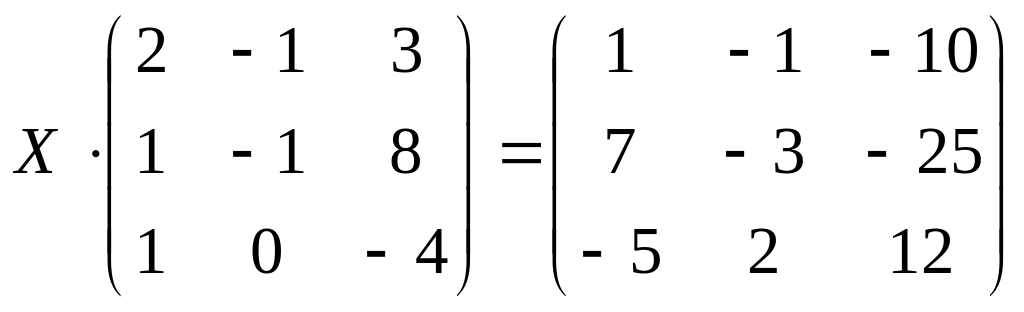 ;
;
4.
a)
![]() ;б)
;б)
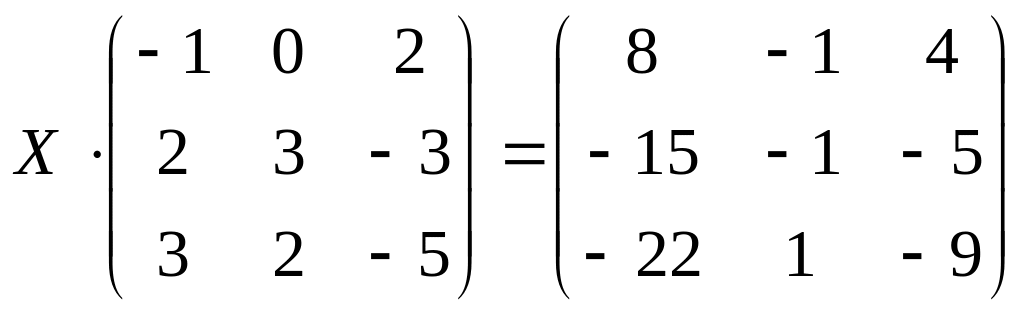 ;
;
5.
а)
![]() ;
б)
;
б)
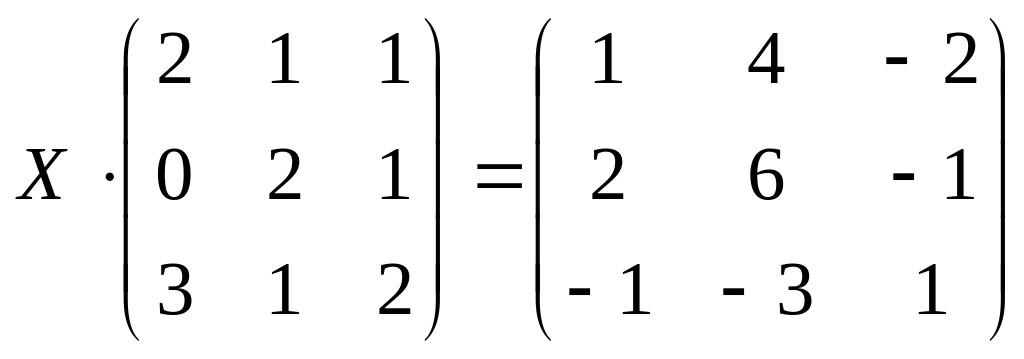 ;
;
6.
а)
![]() ;
б)
;
б)
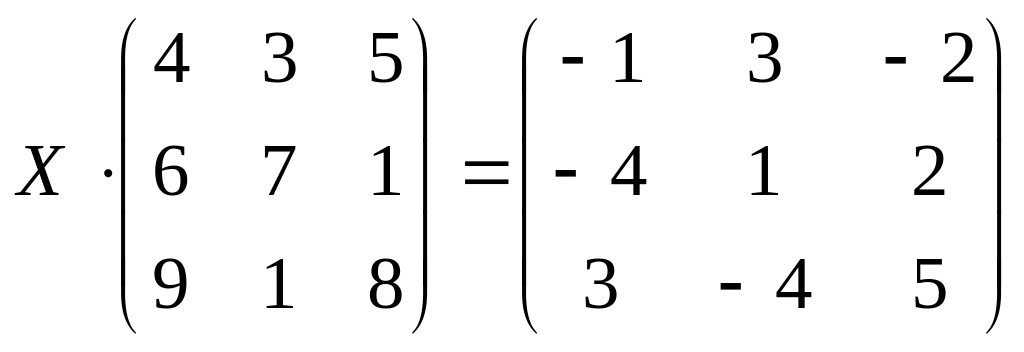 ;
;
7.
a)
![]() ;
б)
;
б)
 ;
;
8.
а)
![]() ;
б)
;
б)
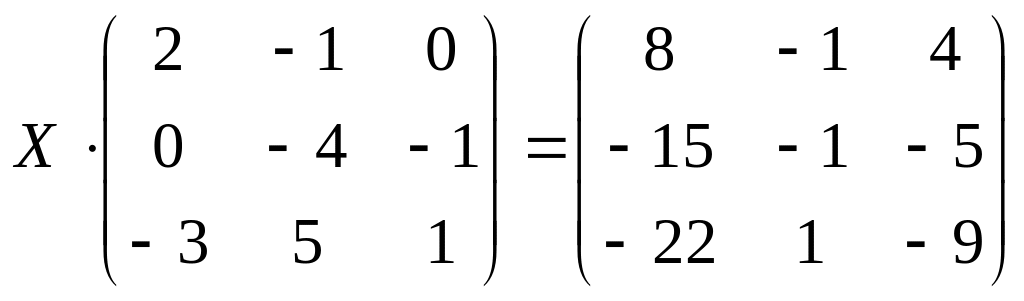 ;
;
9.
а)
![]() ;
б)
;
б)
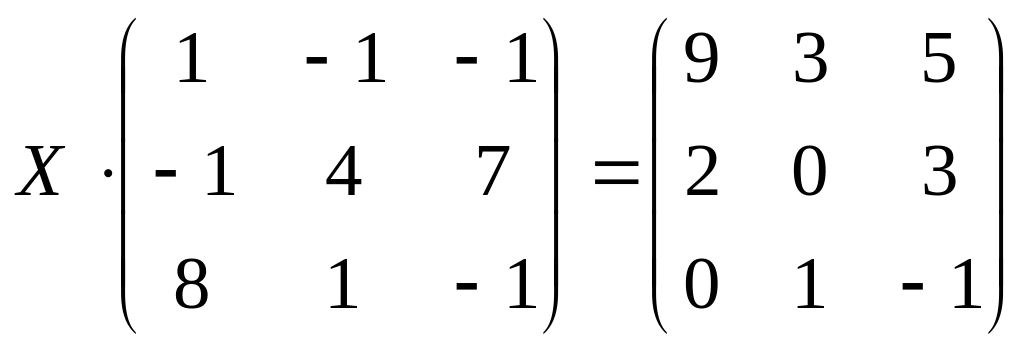 ;
;
10.
а)
![]() ;
б)
;
б)
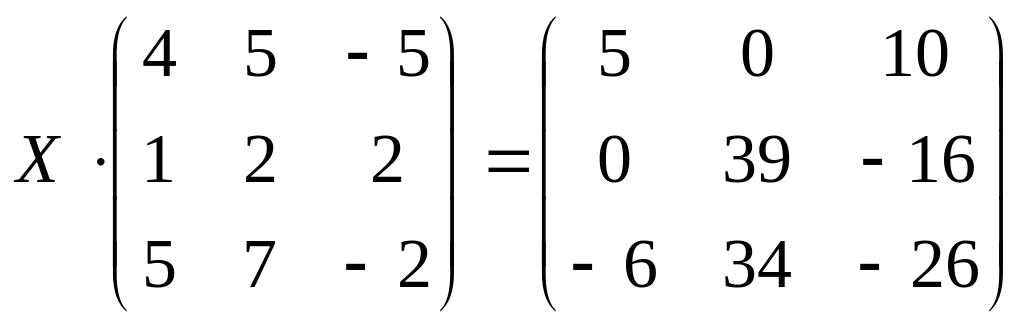 ;
;
11.
а)
![]() ;
б)
;
б)
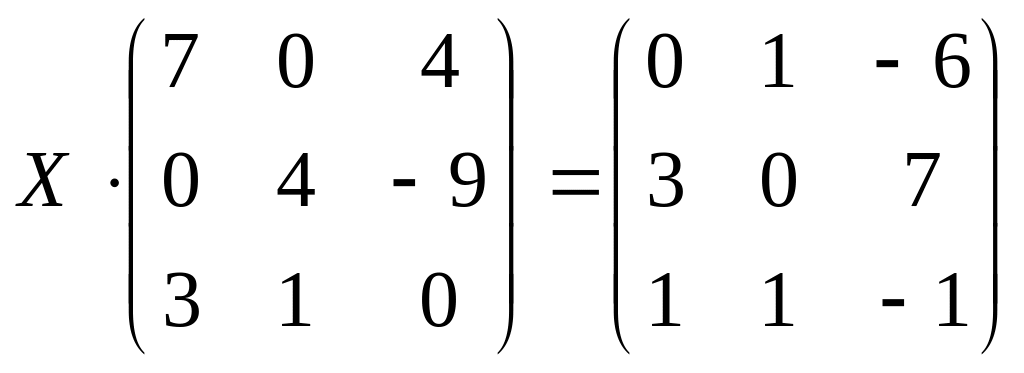 ;
;
12.
а)
![]() ;
б)
;
б)
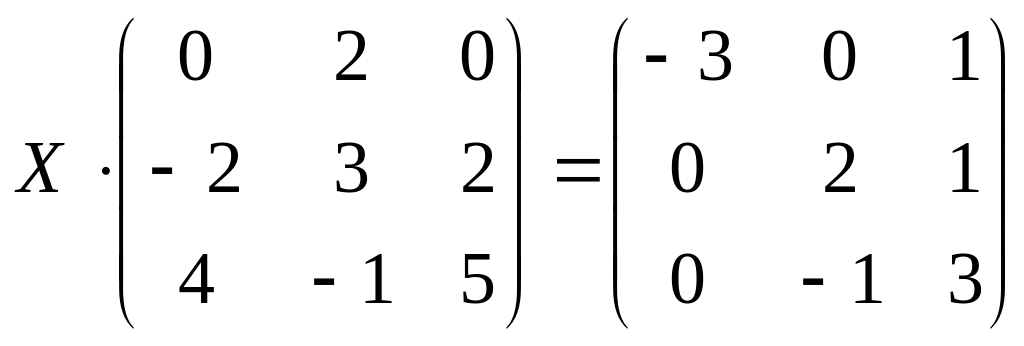 ;
;
13.
а)
![]() ;
б)
;
б)
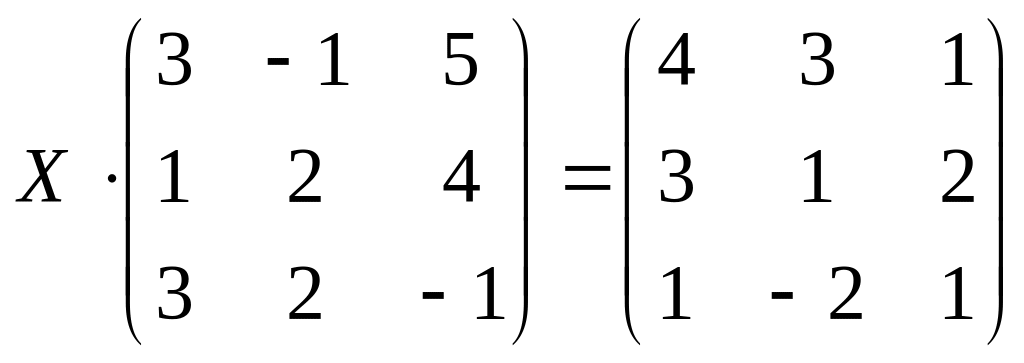 ;
;
14.
а)
![]() ;
б)
;
б)
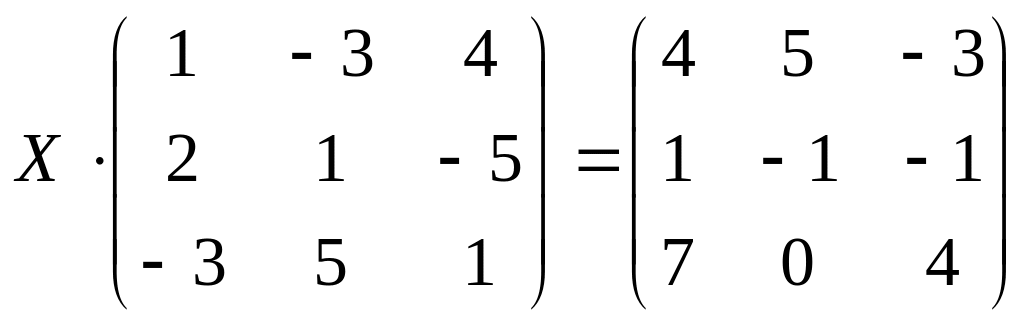 ;
;
15.
а)
![]() ;
б)
;
б)
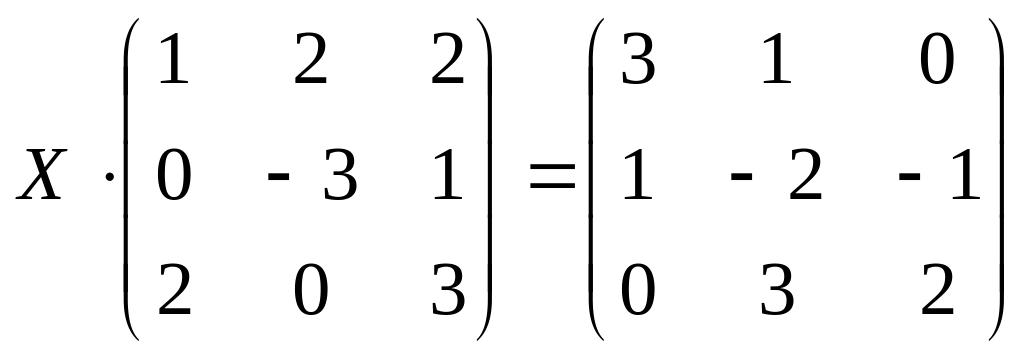 ;
;
16.
а)
![]() ;
б)
;
б)
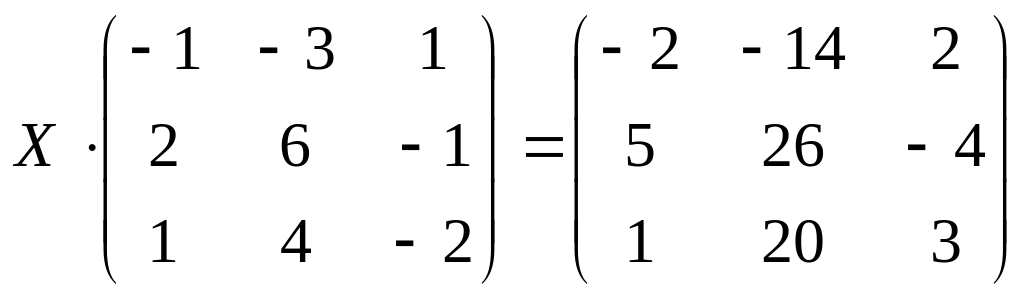 ;
;
17.
а)![]() ;
б)
;
;
б)
;
18.
а)
![]() ;
б)
;
б)
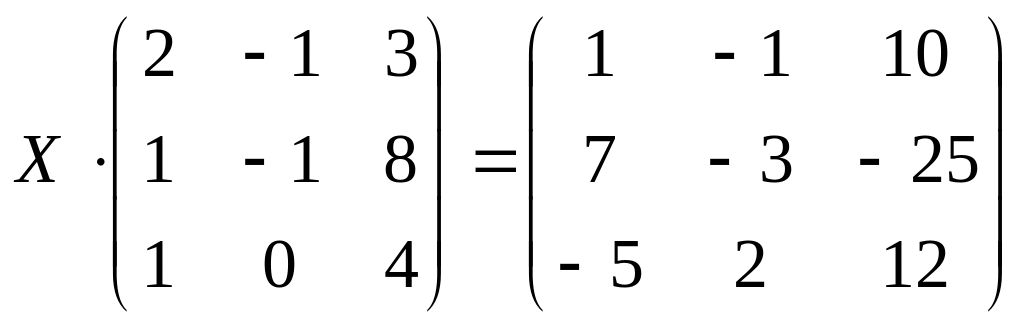 ;
;
19.
а)
![]() ;
б)
;
;
б)
;
20.
а)
![]() ;
б)
;
;
б)
;
21.
а)
![]() ;
б)
;
;
б)
;
22.
а)
![]() ;
б)
;
б)
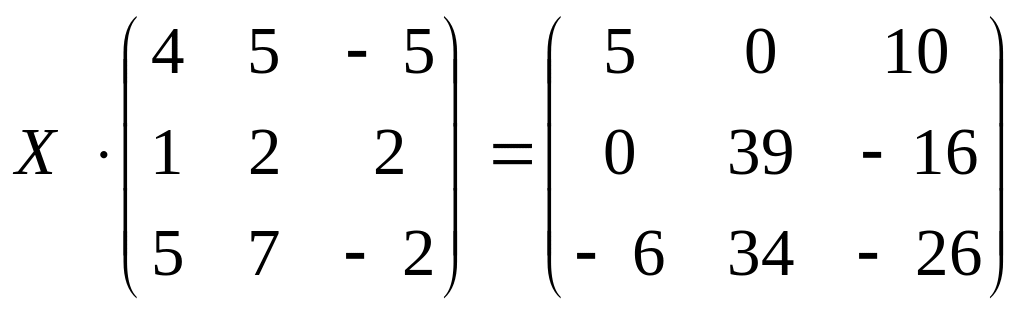 ;
;
23.
а)
![]() ;
б)
;
;
б)
;
24.
а)
![]() ;
б)
;
б)
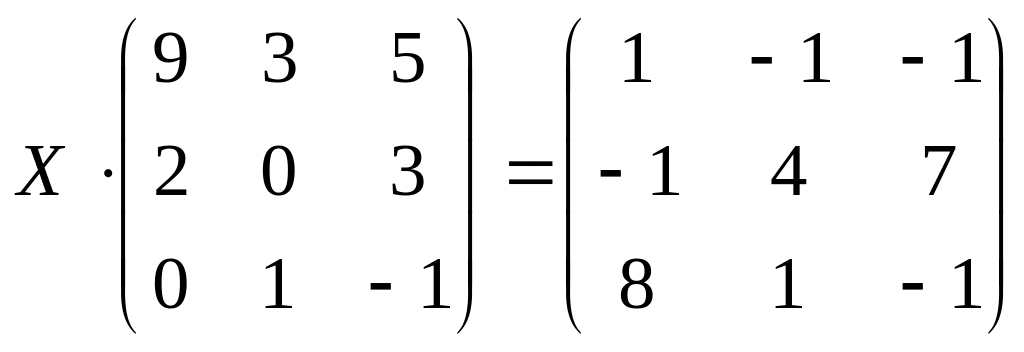 ;
;
25.
а)
![]() ;
б)
;
б)
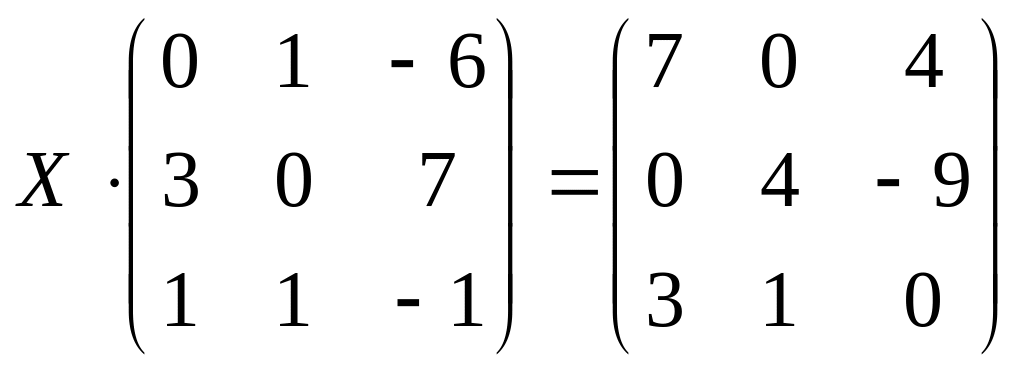 ;
;
26.
а)
![]() ;
б)
;
б)
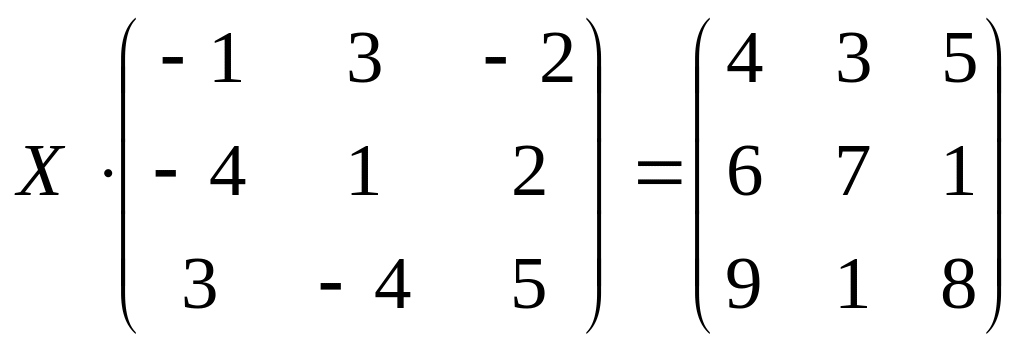 ;
;
27.
а)
![]() ;
б)
;
б)
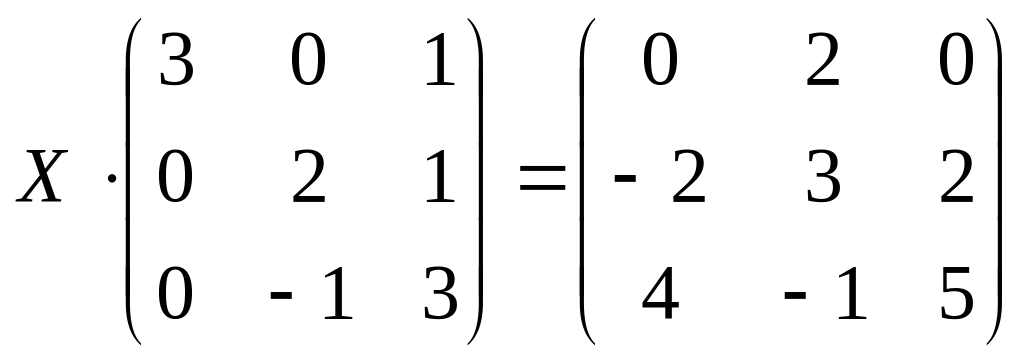 ;
;
28.
а)
![]() ;
б)
;
б)
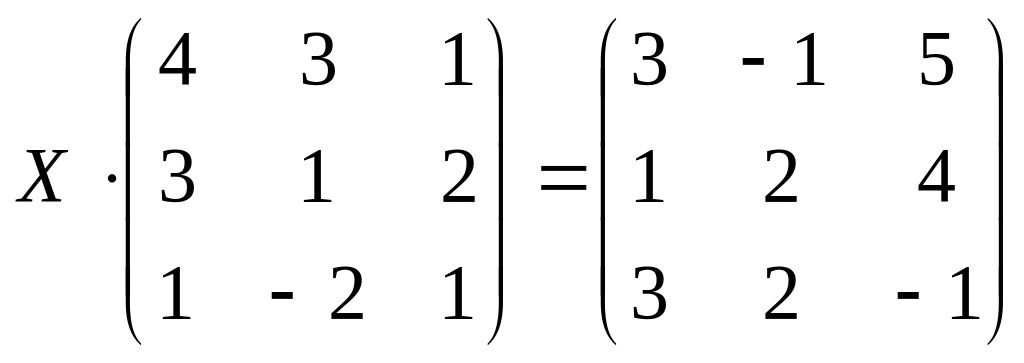 ;
;
29.
а)
![]() ;
б)
;
б)
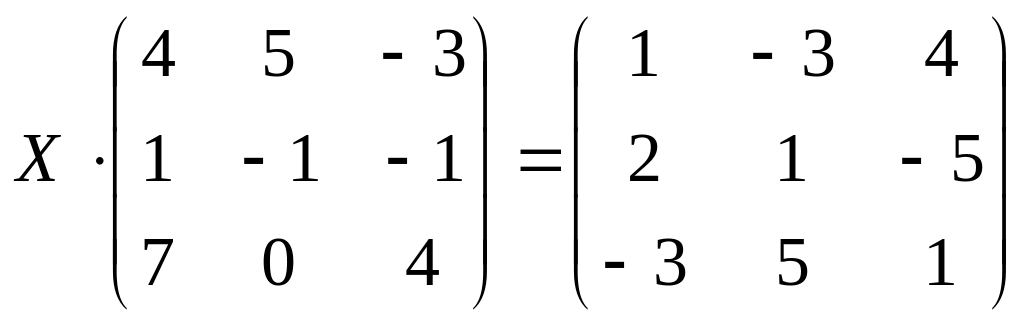 ;
;
30.
а)
![]() ;
б)
;
б)
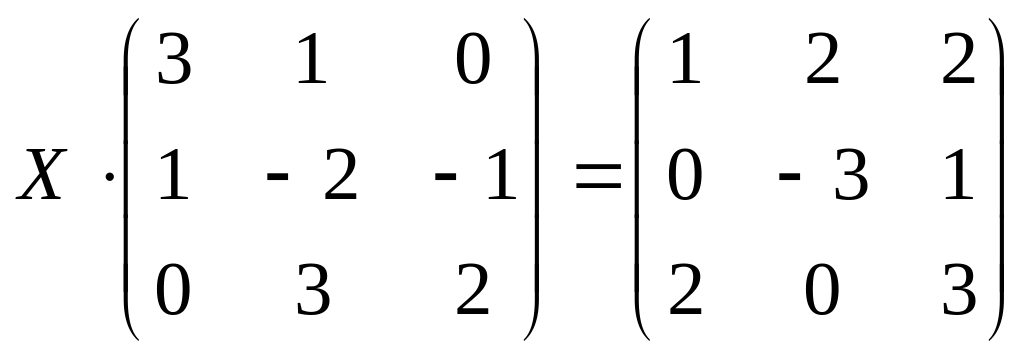 .
.
Задание 6. Исследуйте следующие системы уравнений и найдите их решения:
1.
а)
![]() б)
б)
![]()
2.
а)
![]() б)
б)
![]()
3.
а)
![]() б)
б)
![]()
4.
а)
![]() б)
б)
![]()
5.
а)
![]() б)
б)
![]()
6.
а)
![]() б)
б)
![]()
7.
а)
![]() б)
б)
![]()
8.
а)
![]() б)
б)
![]()
9.
а)
![]() б)
б)
![]()
10.
а)
![]() б)
б)
![]()
11.
а)
![]() б)
б)
![]()
12.
а)
![]() б)
б)
![]()
13.
а)
![]() б)
б)
![]()
14.
а)
![]() б)
б)
![]()
15.
а)
![]() б)
б)
![]()
16.
а)
![]() б)
б)
![]()
17.
а)
![]() б)
б)
![]()
18.
а)
![]() б)
б)
![]()
19.
а)
![]() б)
б)
![]()
20.
а)
![]() б)
б)
![]()
21.
а)
![]() б)
б)
![]()
22.
а)
![]() б)
б)
![]()
23.
а)
![]() б)
б)
![]()
24.
а)
![]() б)
б)
![]()
25.
а)
![]() б)
б)
![]()
26.
а)
![]() б)
б)
![]()
27.
а)
![]() б)
б)
![]()
28.
а)
![]() б)
б)
![]()
29.
а)
![]() б)
б)
![]()
30.
а)
![]() б)
б)
![]()
