
- •Линейная алгебра
- •Место дисциплины в учебном плане
- •Цели и задачи курса
- •1. Матрицы. Основные понятия и определения. Действия над матрицами
- •Действия над матрицами
- •1. Сложение матриц
- •2. Умножение матрицы на число
- •3. Умножение матриц
- •1) Умножение матрицы-строки на матрицу-столбец
- •2) Умножение матриц
- •3) Умножение матрицы-столбца на матрицу-строку
- •Свойства определителей
- •Задачи для самостоятельной работы
- •3. Обратная матрица. Ранг матрицы
- •Правило вычисления ранга матрицы
- •Задачи для самостоятельной работы
- •4. Система линейных алгебраических уравнений
- •4.1. Метод Крамера и матричный способ решения системы линейных уравнений с неизвестными
- •4.2. Метод Гаусса решения системы линейных уравнений с неизвестными (метод последовательного исключения переменных)
- •Второй метод вычисления обратной матрицы.
- •Задачи для самостоятельной работы
- •Тренинг-тесты
- •Вопросы для самопроверки
- •Задачи для контрольных работ
- •Литература Основная
- •Дополнительная
- •Оглавление
Свойства определителей
![]() .
Значение определителя не меняется при
транспонировании матрицы
(замен всех его строк соответствующими
столбцами).
.
Значение определителя не меняется при
транспонировании матрицы
(замен всех его строк соответствующими
столбцами).
![]()
Замечание. Свойство устанавливает равноправность строк и столбцов определителя.
![]() .
При перестановке двух строк значение
определителя меняет знак, сохраняясь
по абсолютной величине.
.
При перестановке двух строк значение
определителя меняет знак, сохраняясь
по абсолютной величине.
![]() .
Определитель с двумя одинаковыми
строками (столбцами) равен нулю.
.
Определитель с двумя одинаковыми
строками (столбцами) равен нулю.
![]() .
Общий множитель всех элементов какой-либо
строки можно вынести за знак определителя
(т.е. при умножении определителя на
число, все элементы какой-либо одной
строки умножаются на это число).
.
Общий множитель всех элементов какой-либо
строки можно вынести за знак определителя
(т.е. при умножении определителя на
число, все элементы какой-либо одной
строки умножаются на это число).
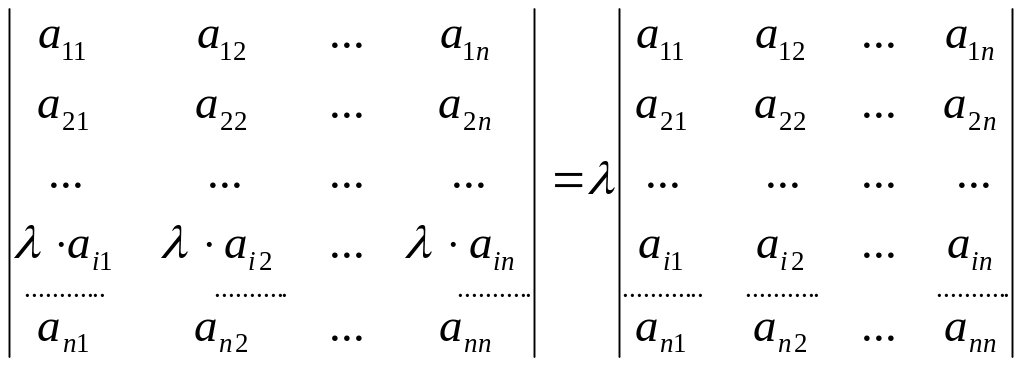
![]() .
Определитель с двумя пропорциональными
строками (столбцами) равен нулю.
.
Определитель с двумя пропорциональными
строками (столбцами) равен нулю.
![]() .
Определитель, имеющий нулевую строку
(столбец), равен нулю.
.
Определитель, имеющий нулевую строку
(столбец), равен нулю.
![]() .
Если два определителя одного порядка
отличаются только элементами одной
строки, то сумма таких определителей
равна определителю с элементами указанной
строки, равными суммам соответствующих
элементов этой строки данных определителей.
.
Если два определителя одного порядка
отличаются только элементами одной
строки, то сумма таких определителей
равна определителю с элементами указанной
строки, равными суммам соответствующих
элементов этой строки данных определителей.
![]() .
Значение определителя не изменяется,
если к элементам какой-либо строки
прибавить соответствующие элементы
другой строки, умноженные на одно и то
же число.
.
Значение определителя не изменяется,
если к элементам какой-либо строки
прибавить соответствующие элементы
другой строки, умноженные на одно и то
же число.
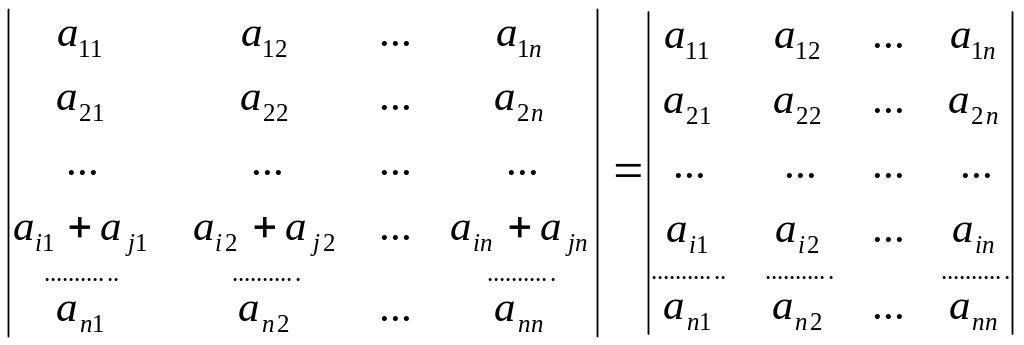
Задачи для самостоятельной работы
2.1.
![]() 2.2.
2.2.
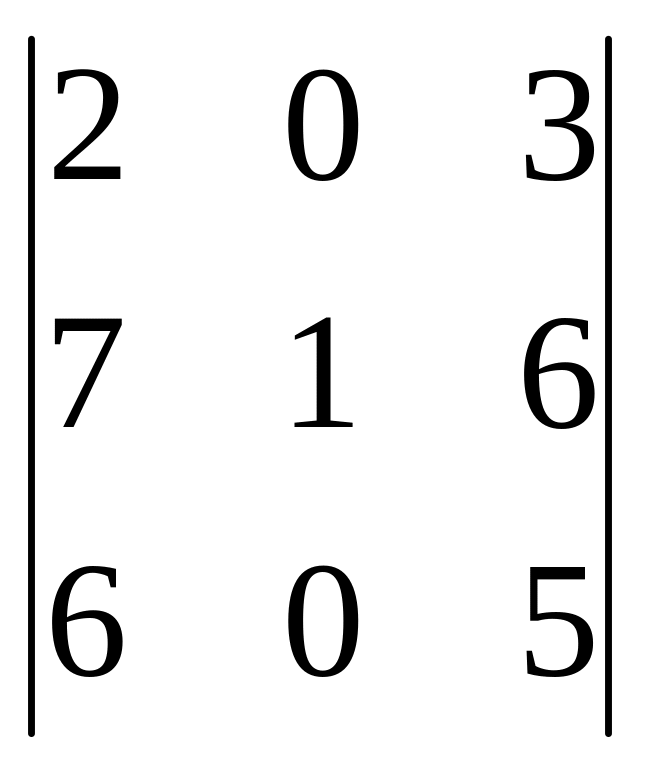
2.3.
 2.4.
2.4.
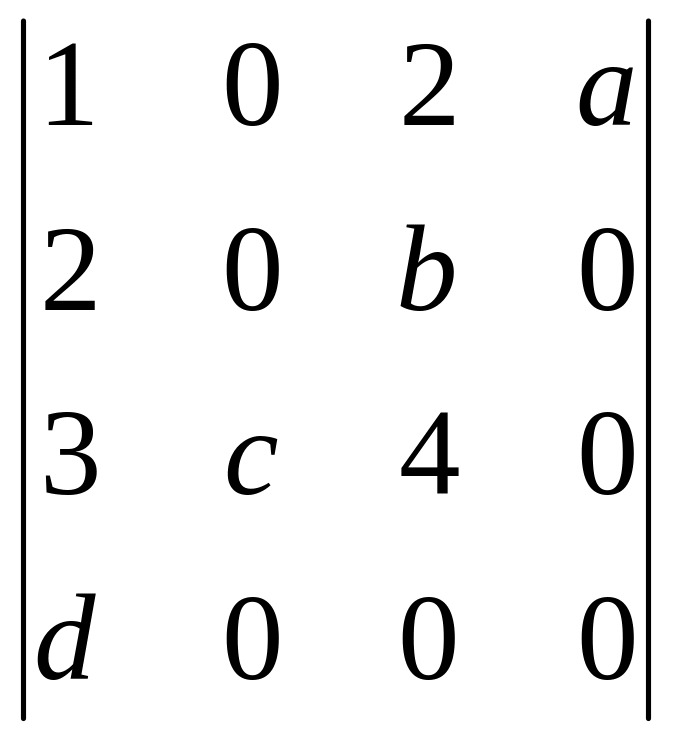
2.5.
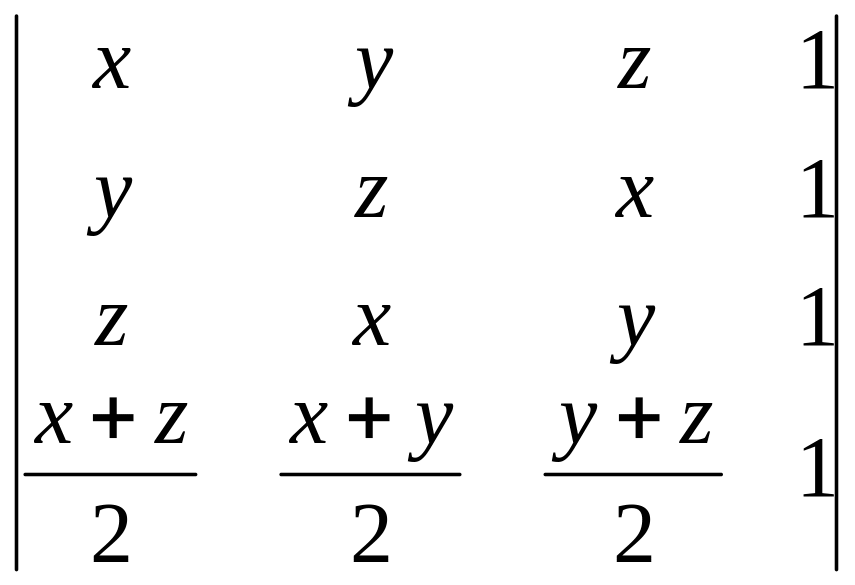 2.6.
2.6.
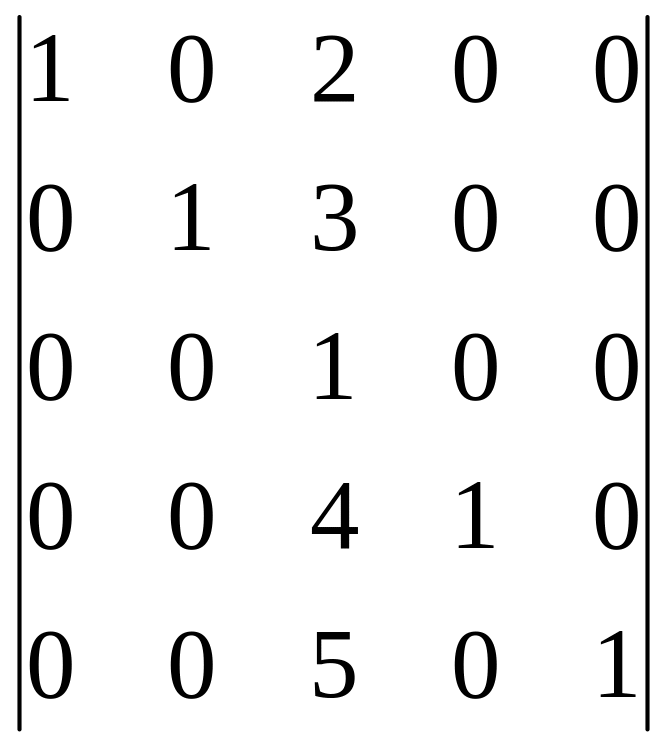
2.7.
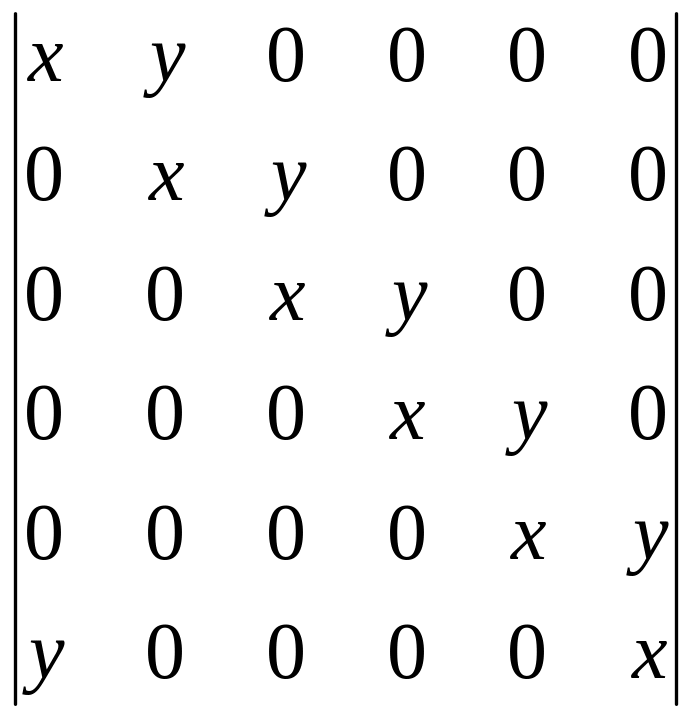
3. Обратная матрица. Ранг матрицы
Определение 3.1.
Квадратная
матрица
![]() называется обратной
по отношению к матрице
,
если выполняется равенство
называется обратной
по отношению к матрице
,
если выполняется равенство
![]() ,
(22)
,
(22)
где – единичная матрица.
Определение 3.2.
Квадратная
матрица
называется невырожденной,
или неособенной, если
![]() .
Если
.
Если
![]() ,
то матрица называется вырожденной
(особенной).
,
то матрица называется вырожденной
(особенной).
Теорема 3.1.
Всякая невырожденная матрица имеет обратную матрицу, определяемую формулой
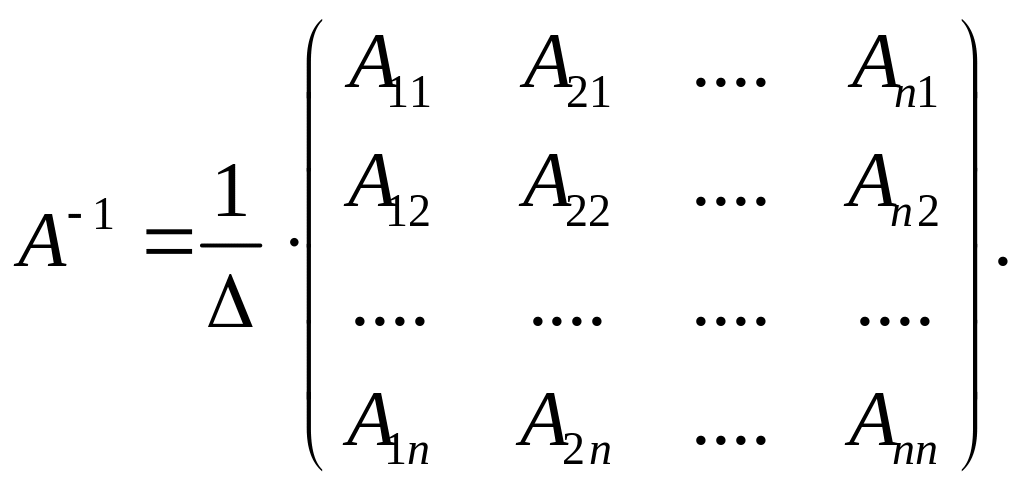 (23)
(23)
Определение 15.
Определитель с элементами, стоящими на пересечении произвольных строк, и столбцов матрицы, называется минором -го порядка этой матрицы.
Замечание. Не путать с минором элемента!
Определение 3.3.
Наивысший порядок отличных от нуля миноров матрицы называется рангом матрицы.
Обозначение:
![]() .
.
Определение 3.4.
Каждый отличный от нуля минор, порядок которого совпадает с рангом матрицы, называется базисным минором.
Правило вычисления ранга матрицы
(метод «окаймляющих миноров»)
При
вычислении ранга матрицы следует
переходить от миноров меньших порядков
к минорам больших порядков. Если уже
найден минор
-го
порядка
,
отличный от нуля, то требуют вычисления
лишь миноры
![]() -го
порядка, окаймляющие минор
:
если все они равны нулю, то ранг матрицы
равен
.
-го
порядка, окаймляющие минор
:
если все они равны нулю, то ранг матрицы
равен
.
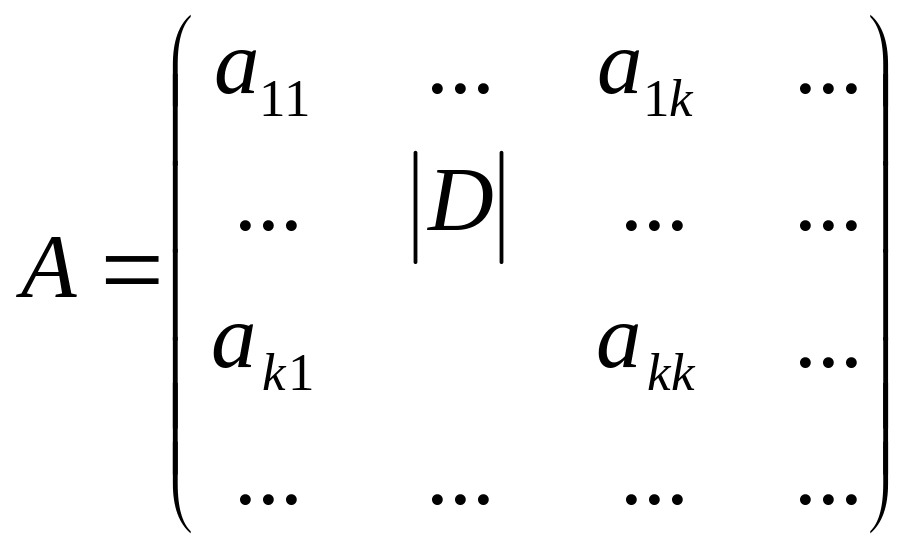 .
.
Определение 3.5.
Элементарными преобразованиями называются следующие преобразования:
Отбрасывание нулевой строки (столбца).
Умножение всех элементов строки (столбца) матрицы на число, не равное нулю.
Изменение порядка строк матрицы.
Прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число.
Транспонирование матрицы.
Замечание. Как правило, получается эквивалентная матрица, не равная данной.
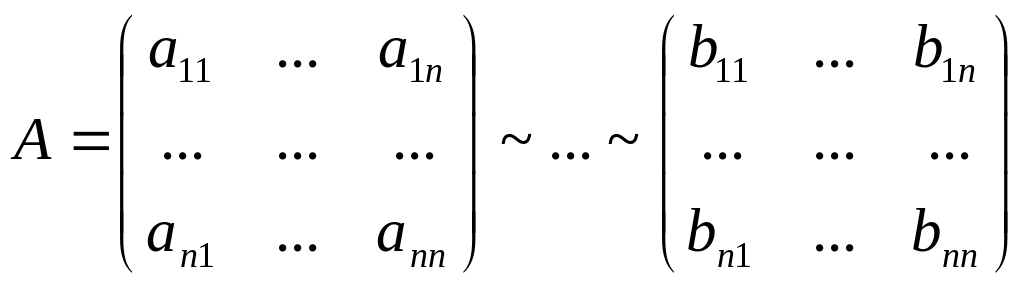 .
.
Определение 3.6.
Матрица, у которой в каждой следующей строке, начиная со второй, первый отличный от нуля элемент стоит правее первого отличного от нуля элемента предыдущей строки, а все нулевые строки (состоящие только из нулей) стоят ниже ненулевых строк (строк, содержащих хотя бы один ненулевой элемент), называется ступенчатой.
Например:
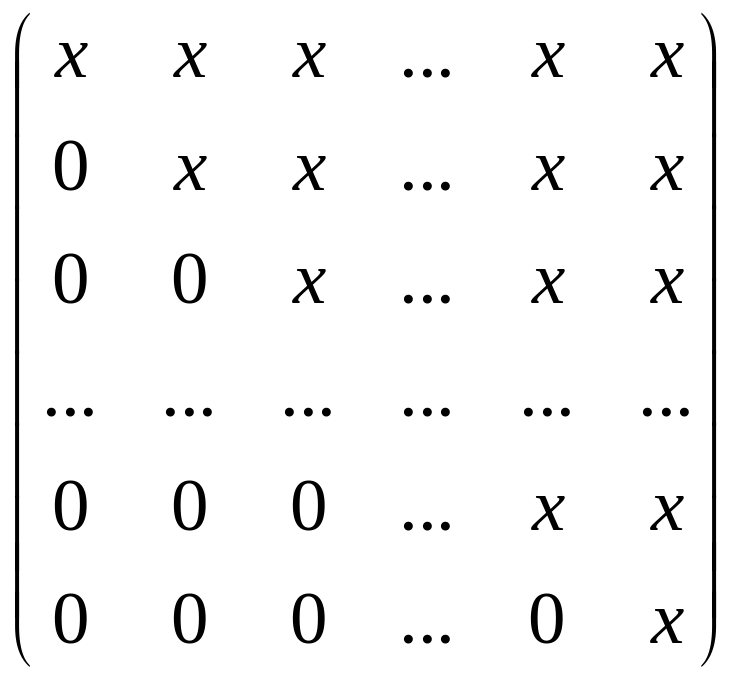 .
.
Пример 3.1.
Определить ранг матрицы
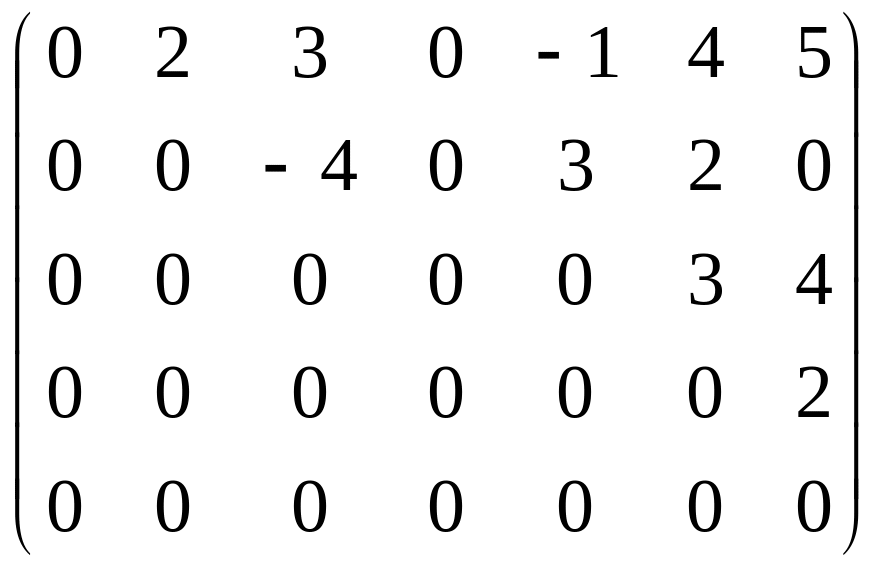 .
.
Решение.
Базисным минором, к примеру, является минор:
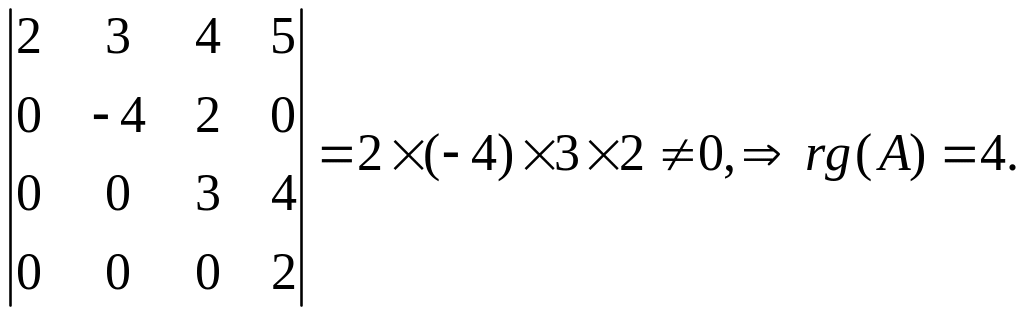
Теорема 3.2.
Элементарные преобразования не изменяют ранга матрицы.
Теорема 3.3. (о ступенчатой матрице).
1). Каждая матрица элементарными преобразованиями строк приводится к ступенчатой матрице.
2). Ранг ступенчатой матрицы равен числу ненулевых строк.
Пример 3.2.
Определить ранг матрицы
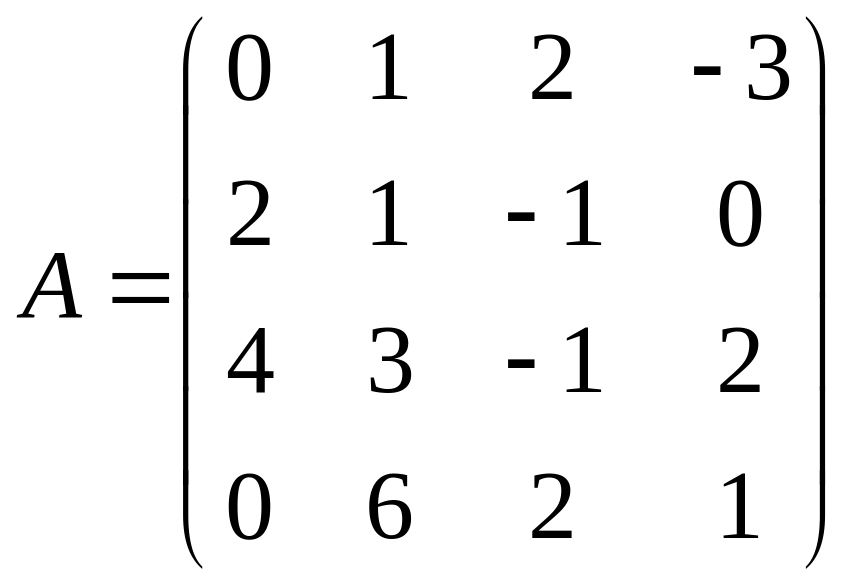 приведением
ее к ступенчатому виду.
приведением
ее к ступенчатому виду.
Решение.

![]() .
.
