ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ГОСУДАРСТВЕННОГО ОБРАЗОВАНИЯ

БАШКИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Н.А. Гарифуллина

Линейная алгебра

Учебно-методическое пособие

У ф а

РИЦ БашГУ

Уфа 2012

УДК 512

ББК 22.14

Печатается по решению кафедры Информационной безопасности ИУБП при Башкирском государственном университете. Протокол № 4 от 13.11.2012 г.

Гарифуллина Н.А.

Линейная алгебра.

Учебно-методическое пособие:/Н.А. Гарифуллина. – Уфа: РИЦ БашГУ, 2012. – 64 с.

Пособие содержит необходимый теоретический материал с примерами и предназначено для более глубокого овладения навыками решения задач студентами дневного и заочного отделений. Представлен материал для решения задач на практических занятиях, для самостоятельной работы студентов, а также для самостоятельного изучения.

УДК 512

ББК 22.14

© Гарифуллина Н.А., сост., 2012

© БашГУ, 2012

Место дисциплины в учебном плане

Дисциплина «Математика» занимает одно из центральных мест в учебных планах, она входит в цикл математических и естественнонаучных дисциплин. Основные требования к содержанию дисциплины определены государственным образовательным стандартом высшего профессионального образования. Для освоения дисциплины достаточно знаний и умений в объеме элементарной математики. Математика играет важную роль в освоении естественнонаучных, инженерно-технических и экономических дисциплин. Математика является не только орудием количественного расчета, но также методом точного исследования и средством предельно четкой формулировки понятий и проблем. Математика является не только мощным средством решения прикладных задач и универсальным языком науки, но также и элементом общей культуры. Поэтому математическое образование следует рассматривать как важнейшую составляющую в системе фундаментальной подготовки современного экономиста.

Цели и задачи курса

Линейная алгебра составляет начальный раздел общего курса математики в вузе. Целью данного раздела является ознакомление с такими фундаментальными математическими понятиями, как матрица, ранг матрицы, обратная матрица, определители, решение системы линейных уравнений, метод Гаусса. Задачей курса является приобретение знаний по основным математическим понятиям и навыков по решению различных задач данного раздела.

1. Матрицы. Основные понятия и определения. Действия над матрицами

Многие задачи математики (и не только математики) приводят к рассмотрению специальных таблиц (в общем случае прямоугольных), составленных из чисел

,

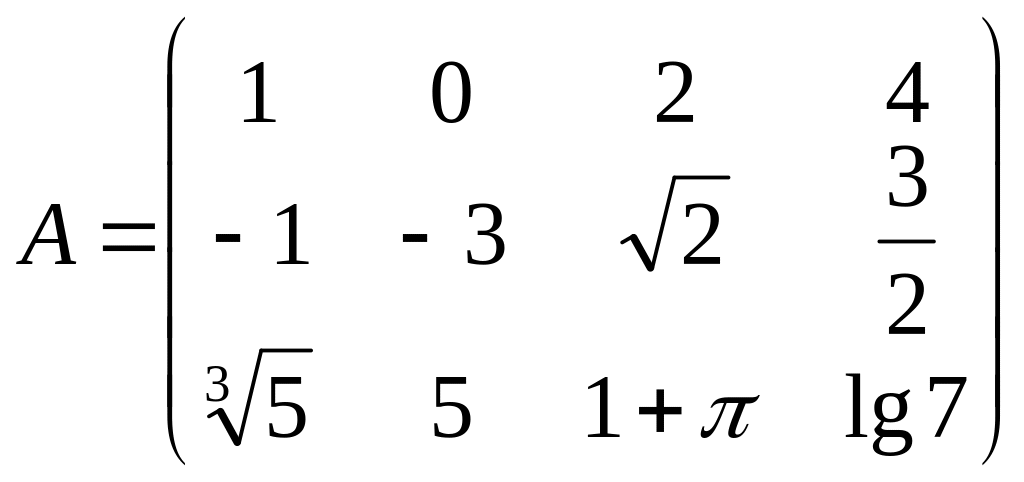В этой таблице 3 строки и 4 столбца, ее полезно представить схематично.

Определение 1.1.

Прямоугольная таблица чисел или букв, состоящая из строк и столбцов называется матрицей порядка .

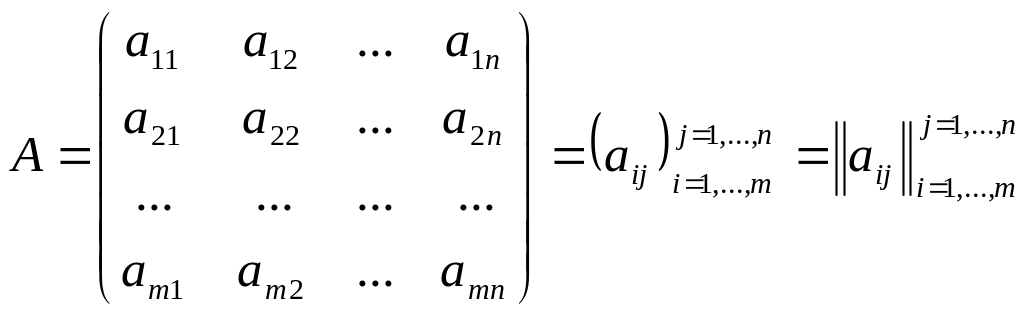. (1)

Числа ( ) называются элементами матрицы (здесь первый индекс – номер строки, а второй – номер столбца, на пересечении которых находится данный элемент).

Пример 1.1.

Матрицы, составленные из чисел, возникают при рассмотрении систем линейных уравнений

(2)

Пример 1.2.

Рассмотрим систему . (*)

Системе линейных алгебраических уравнений (*) соответствуют две матрицы:

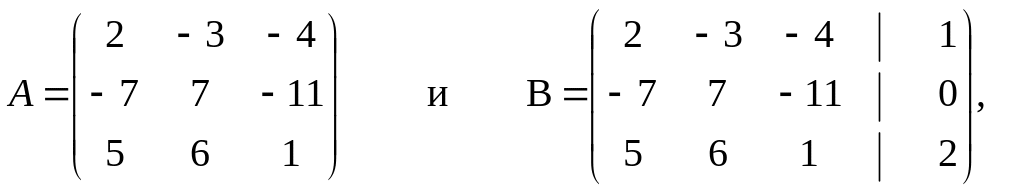
А называется матрицей коэффициентов системы (*), В – её расширенной матрицей. Ясно, что система (*) вполне определяется заданием матрицы В.

Определение 1.2.

Частным случаем – матрицы являются и такие матрицы, как , это так называемая матрица-строка.

Определение 1.3.

Матрица вида 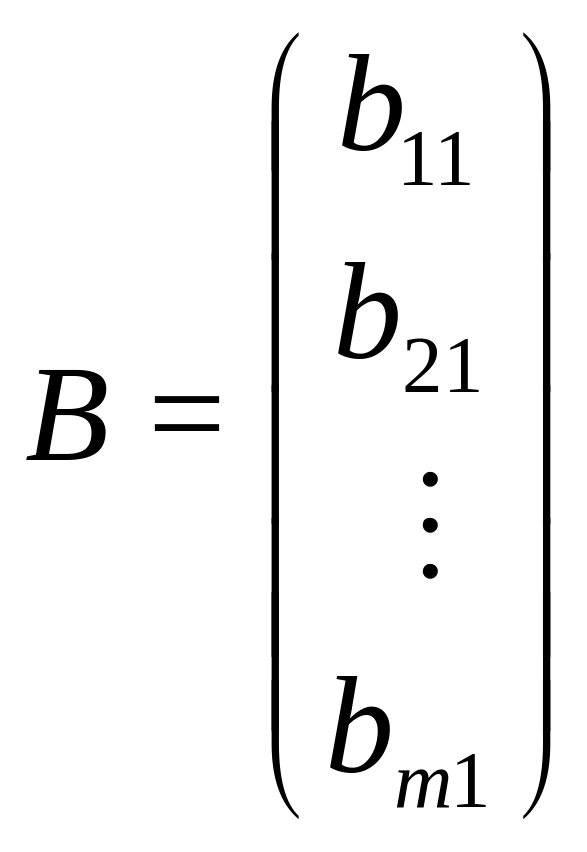называется матрица-столбец.

Определение 1.4.

Матрица, полученная из матрицы заменой строк на столбцы, называется транспонированной матрицей и обозначается .

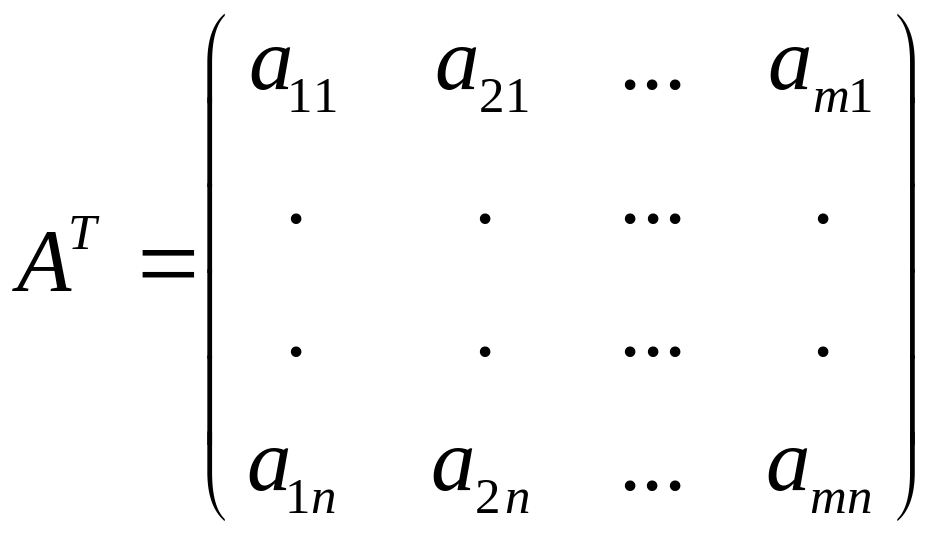. (3)

Определение 1.5.

Рассмотрим две матрицы одинакового строения: , (они имеют одинаковое число строк , и одинаковое число столбцов ). Матрица называется равной матрице , если они равны поэлементно.

,

т.е. соответствующие элементы матриц и равны.

Пример 1.3.

Например, если

,

то а₁₁ = 1, a₁₂ = 0, a₁₃ = 2, a₁₄ = -1; a₂₁ = 3, a₂₂ = -4, a₂₃ = 1, a₂₄ = -5.

Определение 1.6.

Матрица называется нулевой или нуль-матрицей, если все элементы матрицы равны нулю.

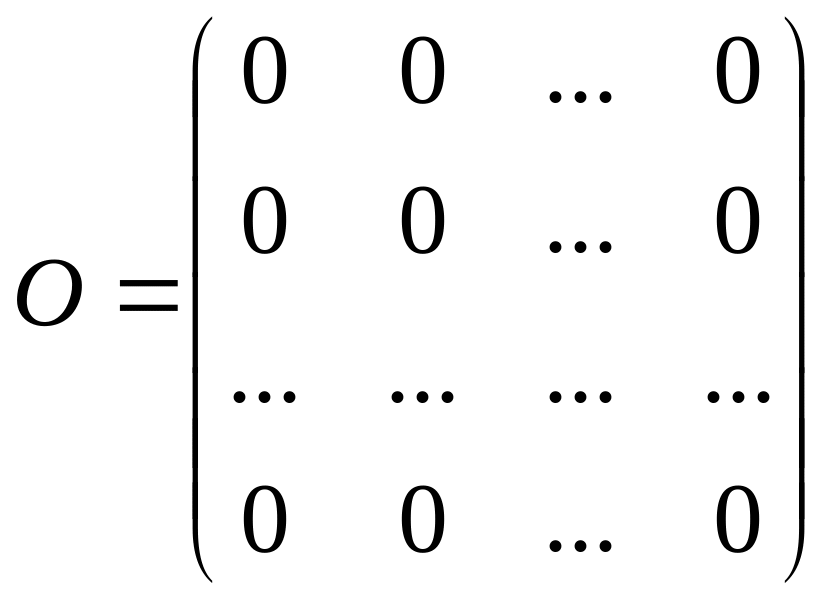
Определение 1.7.

Матрица 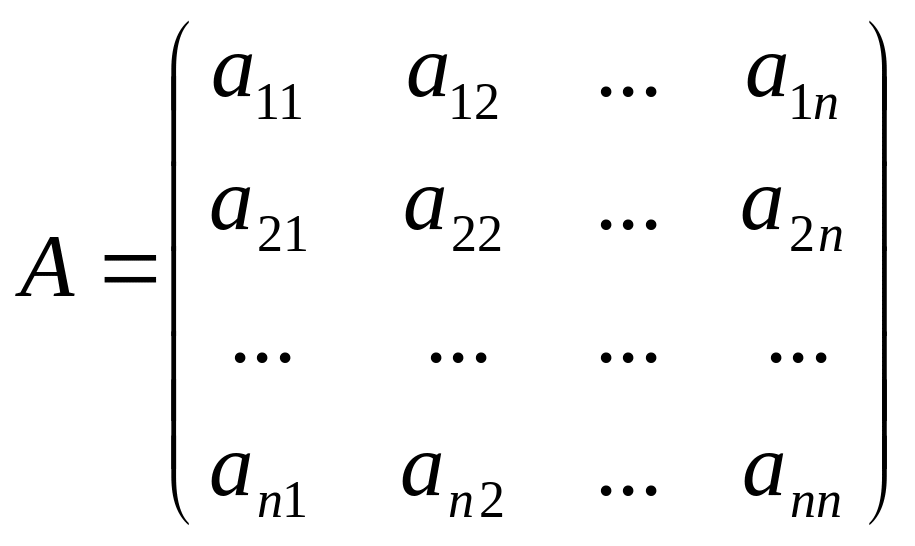размера называется квадратной матрицей -го порядка.

• Замечание. Диагональ 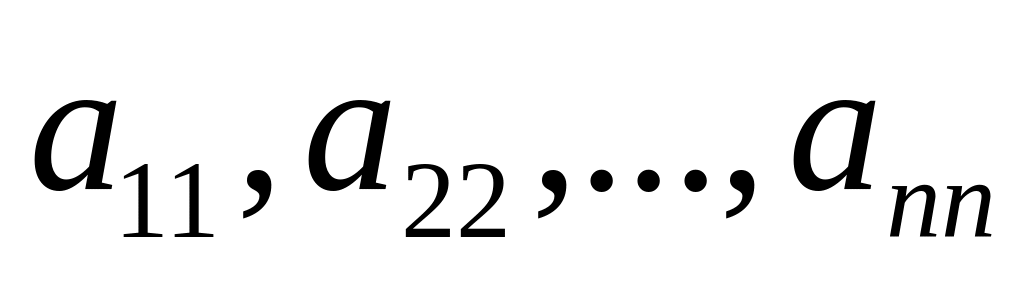называется главной диагональю квадратной матрицы (для главной диагонали характерно свойство 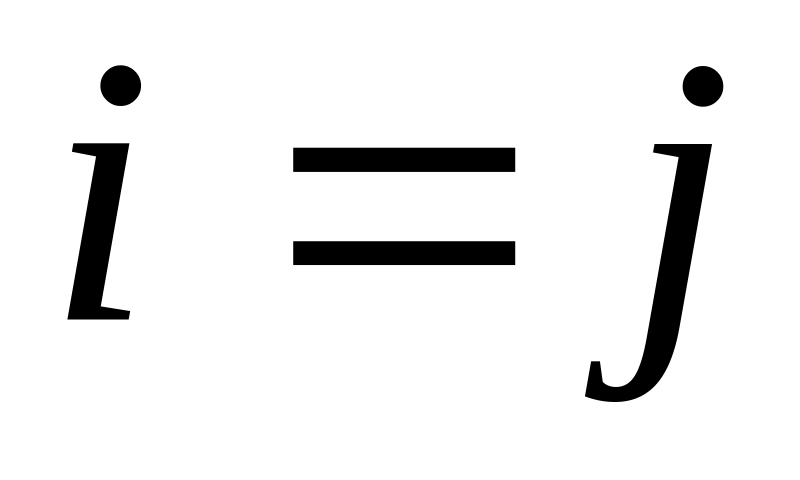), а диагональ 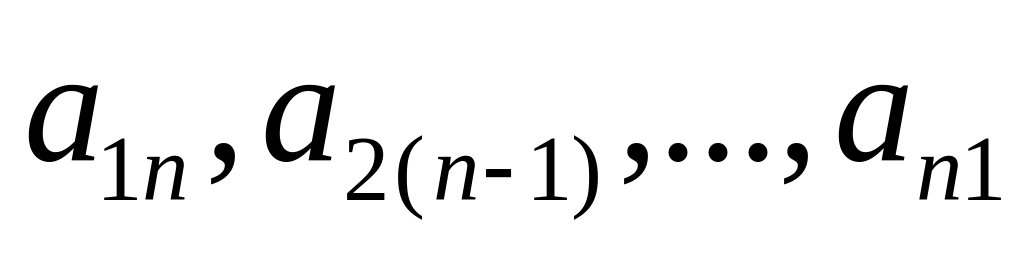– побочной диагональю (для побочной диагонали характерно свойство ).

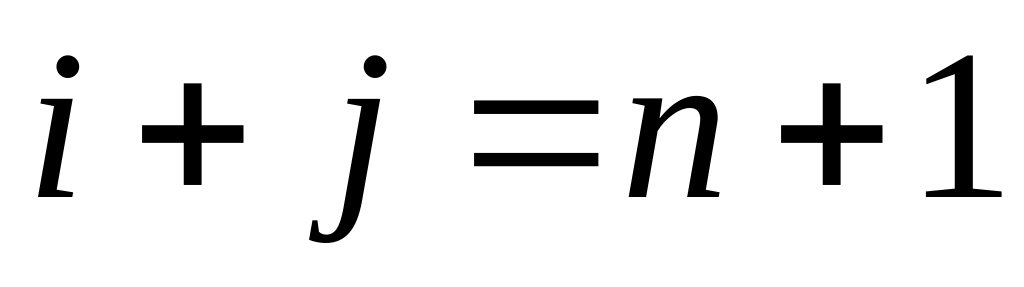Определение 1.8.

Квадратная матрица называется единичной, если элементы главной диагонали равны единице, а остальные элементы равны нулю.

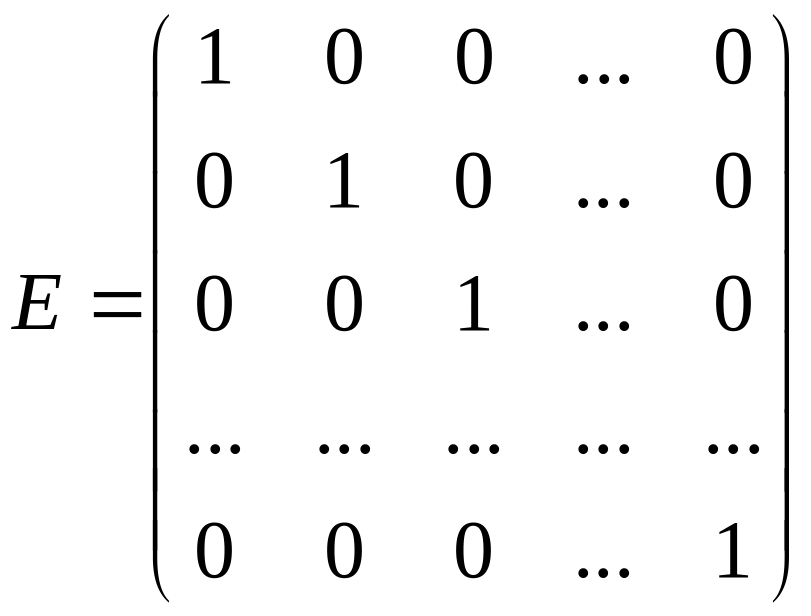
Определение 1.9.

Квадратная матрица называется диагональной, если все элементы, кроме главной диагонали, равны нулю (хотя часть из диагональных элементов могут быть нулями).

Определение 1.10.

Выделим из множества квадратных матриц так называемые треугольные матрицы:

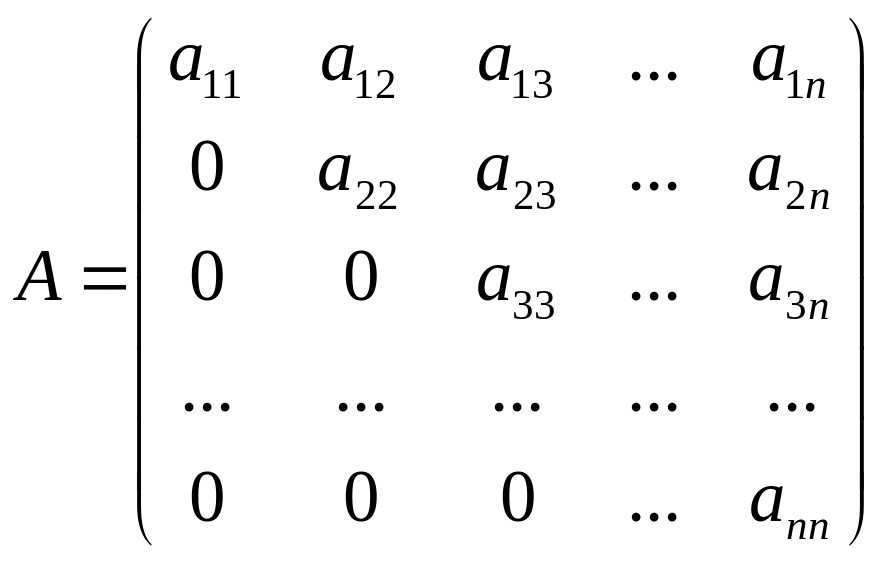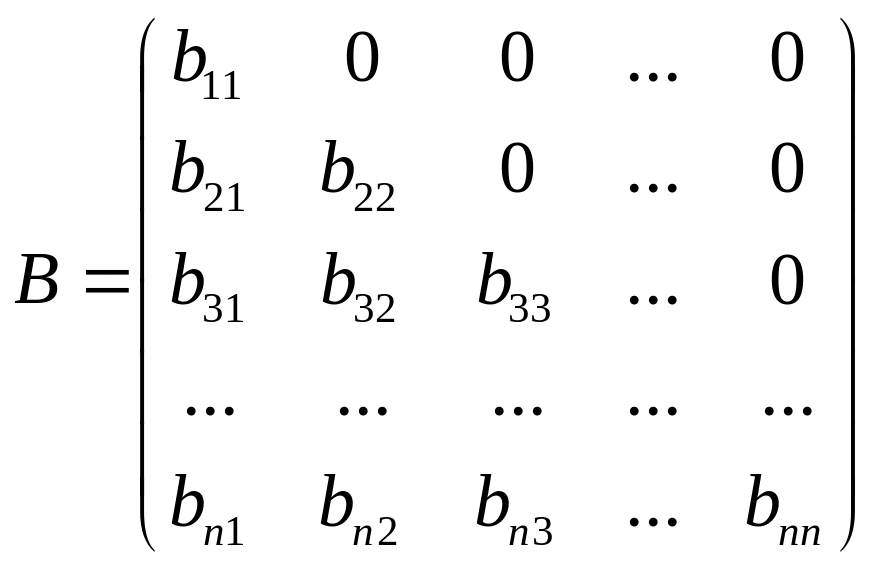- верхнетреугольная,

- нижнетреугольная.